2D Shapes (Cambridge (CIE) IGCSE International Maths)

Properties of 2D Shapes

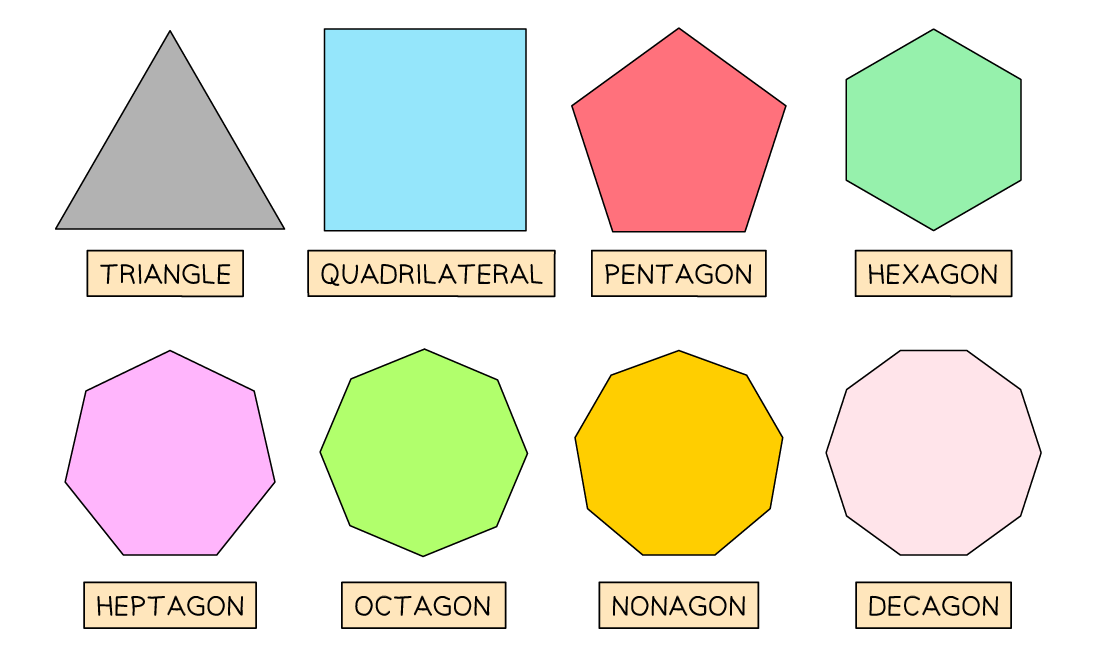
What are the names of common 2D shapes?

• You should know the general names of all the 2D polygons

  • A triangle has 3 sides

  • A quadrilateral has 4 sides

  • A pentagon has 5 sides

  • A hexagon has 6 sides

  • A heptagon has 7 sides

  • An octagon has 8 sides

  • A nonagon has 9 sides

  • A decagon has 10 sides

  • A polygon is a flat (plane) shape with n straight sides

    • A regular polygon has all sides the same length and all angles the same size  

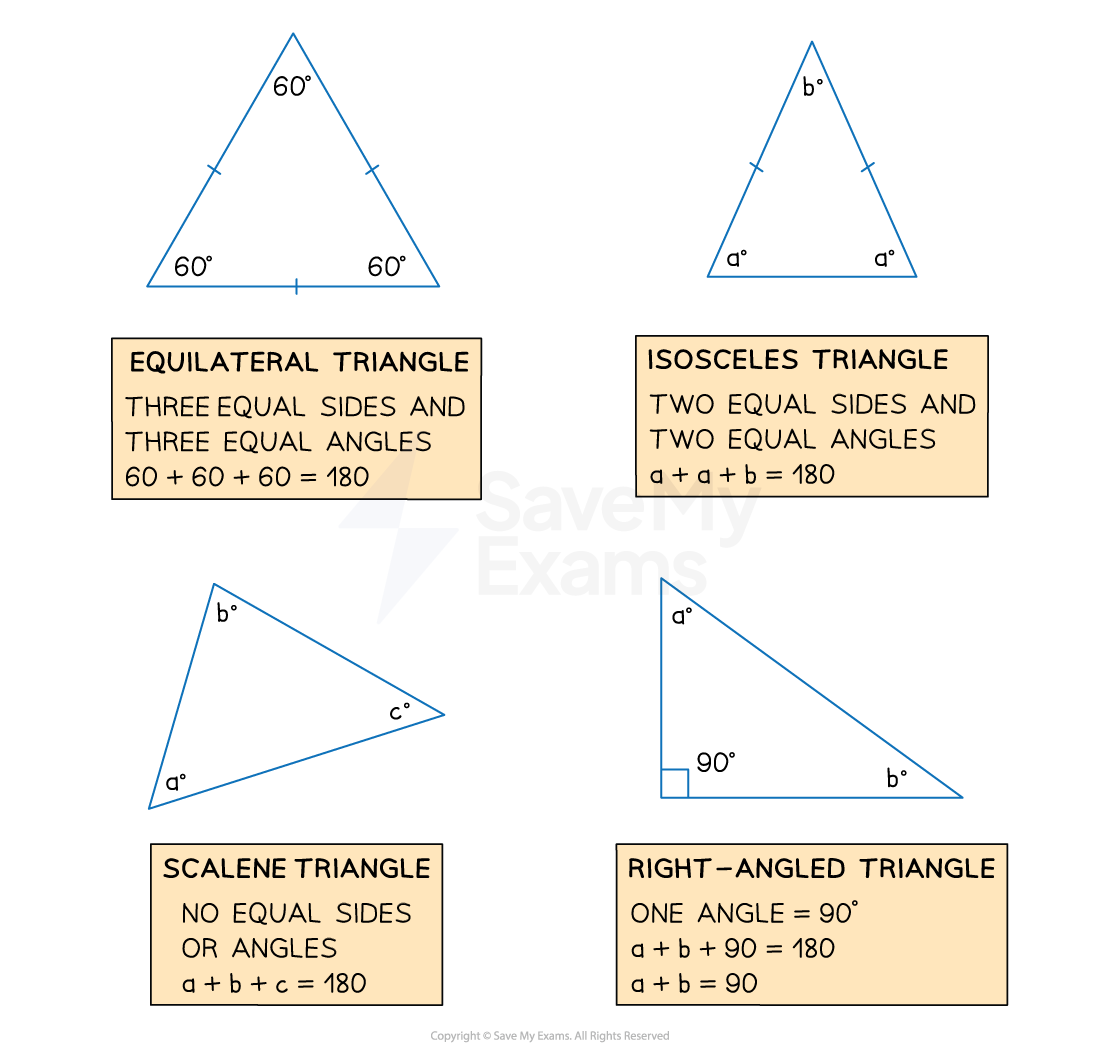
What are the names of the different types of triangles?

• You should know the names and properties of the different types of triangles

  • An equilateral triangle has 3 equal sides and 3 equal angles

  • An isosceles triangle has 2 equal sides and 2 equal angles

  • A right-angled triangle has one 90° angle

  • A scalene triangle has 3 sides all of different lengths

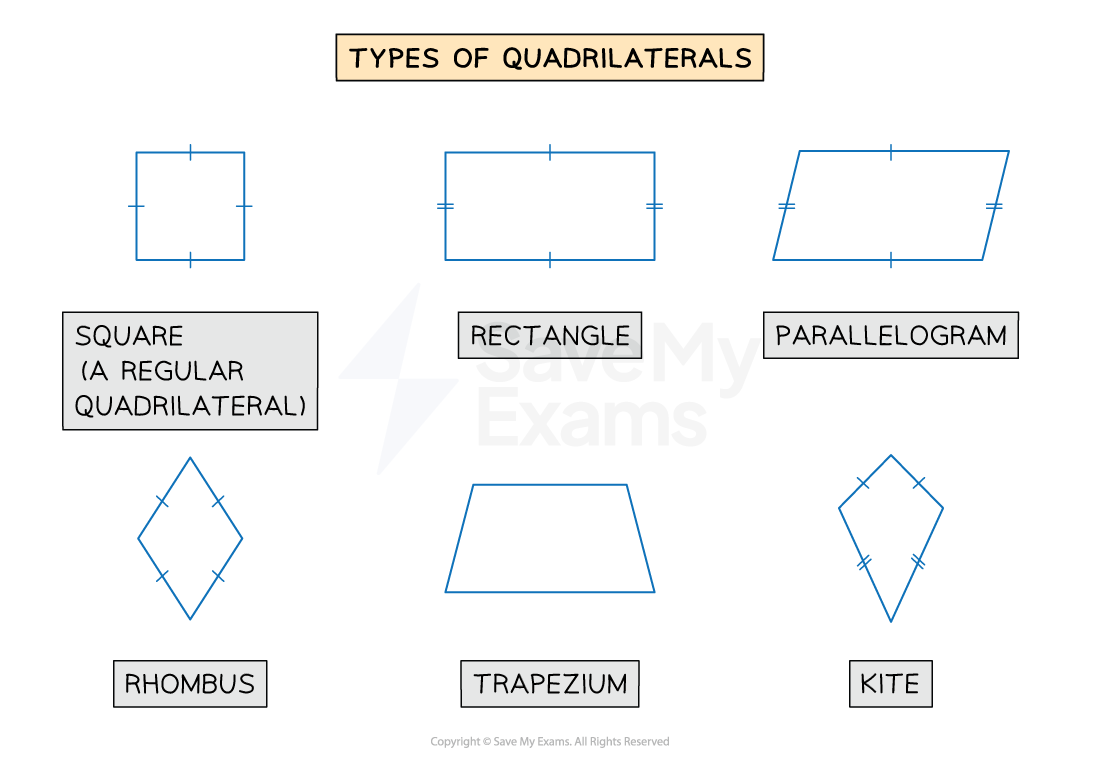
What are the names of the different types of quadrilaterals?

• You should know the names and properties of the different types of quadrilaterals

  • These are squares, rectangles, parallelograms, rhombuses, trapeziums and kites

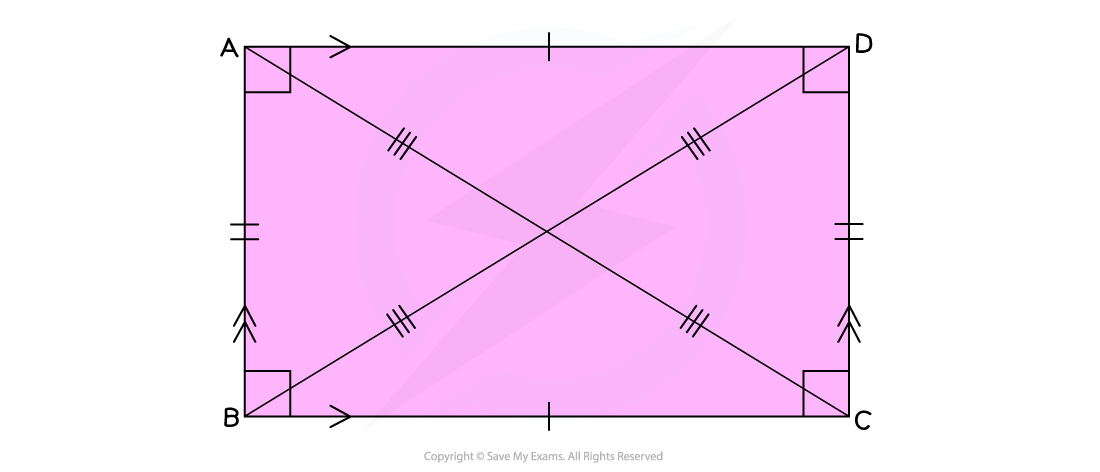
What are the properties of rectangles and squares?

• Rectangles and squares have four equal right angles (90°)

• Rectangles have two pairs of equal length, parallel sides

  • Squares are just regular rectangles; all four of their sides are equal

• The diagonals of a rectangle bisect each other at the centre of the rectangle

  • This means that they cut each other in half

  • The intersecting diagonals form two pairs of angles at the centre
    

    • In a square, all four of these angles will be equal to 90°

• Pythagoras’ theorem can be used to find the length of the diagonal of a square or rectangle

  • The diagonal forms the hypotenuse of a right-angled triangle

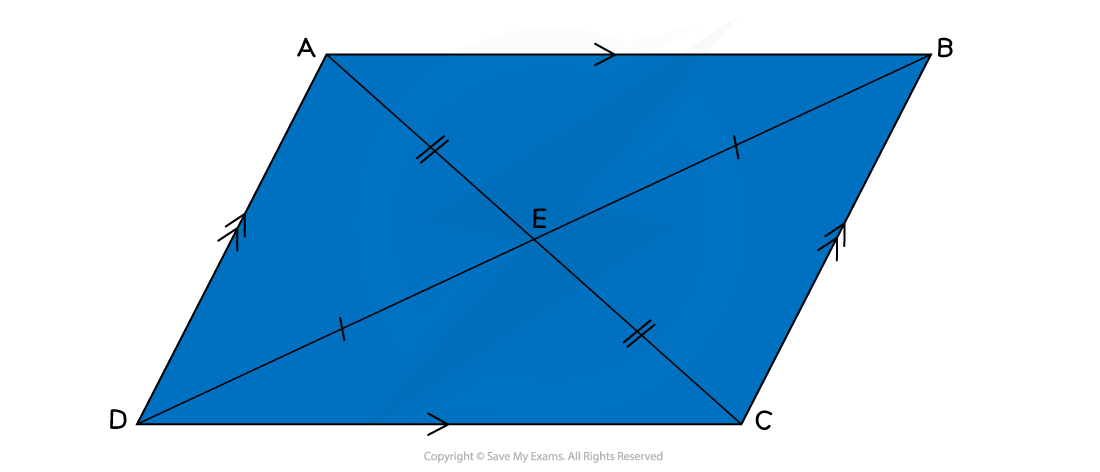
What are the properties of parallelograms and rhombuses?

• Parallelograms and rhombuses (rhombi) have two pairs of equal, opposite, angles

• Parallelograms and rhombuses have two pairs of opposite, parallel sides

• Rhombuses have four sides of the same length

  • This means a rhombus is a regular parallelogram

    • A square is also a regular rhombus

• The diagonals of a parallelogram bisect each other, forming two pairs of opposite angles

• The diagonals of a rhombus bisect each other at right angles (90°)

  • This means that they cut each other in half

  • The diagonals will not be of equal length

    • On the diagram below, the diagonal AC is shorter than the diagonal DB

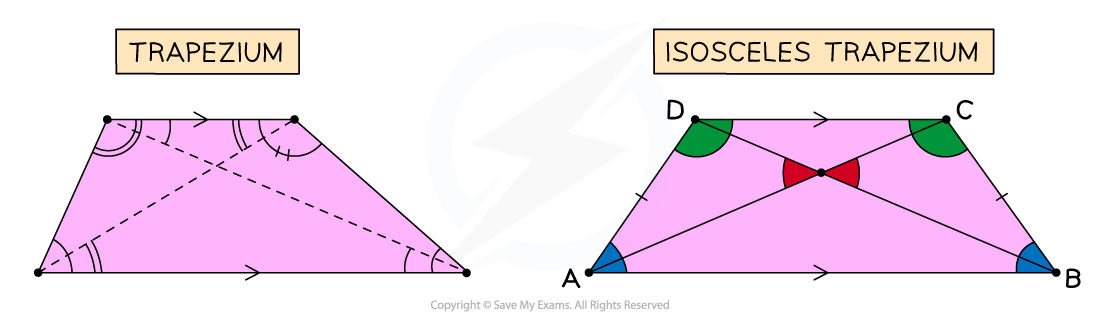
What are the properties of trapeziums?

• Trapeziums have one pair of opposite, parallel sides

  • These are not of equal length

• Trapeziums may not have any equal angles

  • As with all quadrilaterals, the angles add up to 360°

• If a trapezium has a line of symmetry, it is classed as isosceles

  • Isosceles trapeziums have two pairs of equal angles

  • The non-parallel sides in an isosceles trapezium will be equal length

  • An isosceles trapezium has two diagonals of equal length

What are the properties of kites?

• Kites have one line of symmetry, known as their main diagonal

• The angles opposite the main diagonal are equal

  • These are angles ABC and ADC on the diagram below

• The diagonals of a kite bisect each other at right angles (90°)

  • This means that they cut each other in half

  • The diagonals will not be of equal length

• Kites have no parallel sides

• Kites have two pairs of equal length, adjacent sides

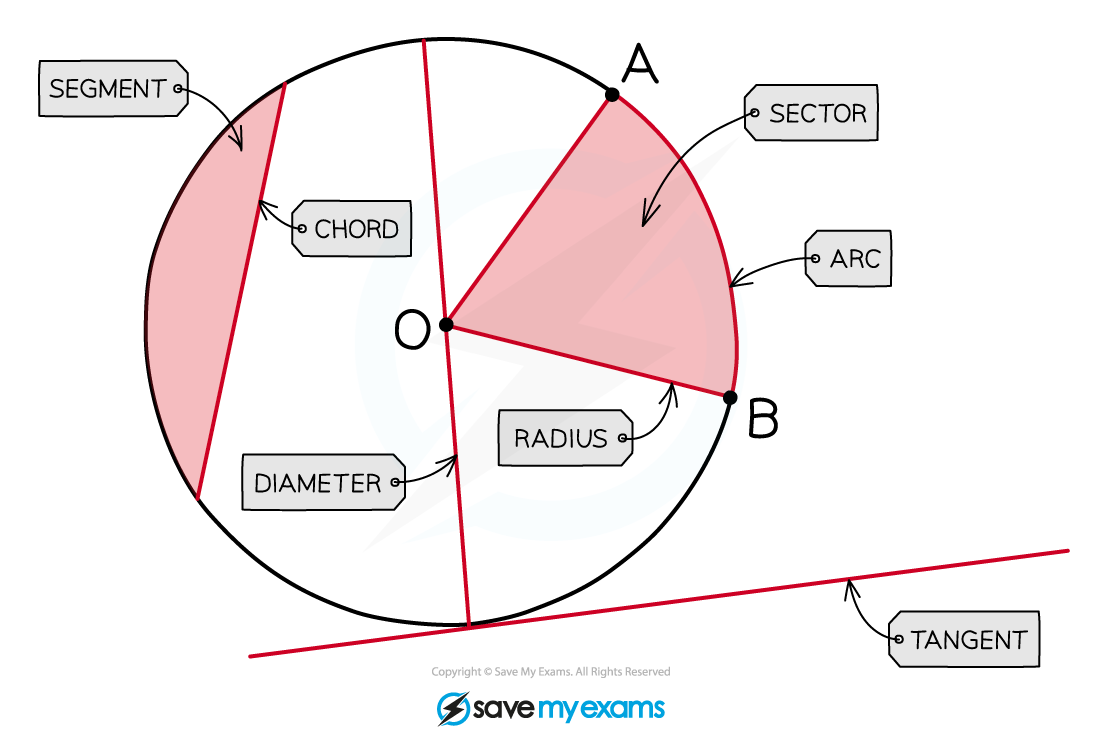
What terms related to circles do I need to know?

• Circles have several specific terms that you need to be familiar with:

  • A circle's perimeter is called a circumference

  • Its line of symmetry is called a diameter

  • The line from the centre of the circle to its circumference is called a radius

    • The diameter is equal to 2 × the radius

  • A portion of the circumference is called an arc

  • A portion of the area, contained between two radii and an arc, is called a sector

  • A line between two points on the circumference is called a chord

  • The area formed between a chord and an arc is called a segment

  • A line which intersects the circumference at one point only, is called a tangent

• The ratio  is equal to 𝝅 (3.14159...)

• Circles have many angle properties and you will need to learn some of them

  • These properties are known as circle theorems