Drawing Straight Line Graphs (Cambridge (CIE) IGCSE International Maths)

Revision Note

Reviewed by: Dan Finlay

Did this video help you?

Drawing Linear Graphs

How do I draw a straight line from a table of values?

You may be given a table of values with no equation
Use the x and y values to form a point with coordinates (x, y)
- Then plot these points
- Use a ruler to draw a straight line through them
  - All points should lie on the line
For example
- The points below are (-3, 0), (-2, 2), ... etc

$x$	-3	-2	-1	0	1	2	3
$y$	0	2	4	6	8	10	12

How do I draw a straight line using y = mx + c?

Use the equation to create your own table of values
- Choose points that are spread out across the axes given
For example, plot y = 2x + 1 on axes from x = 0 to x = 10
- Substitute in x = 0, x = 5 and x = 10 to get y coordinates
  - Then plot those points

$x$	0	5	10
$y$	1	11	21

How do I draw a straight line without using a table of values?

Assuming the equation is in the form y = mx + c
Start at the y-intercept, c
Then, for every 1 unit to the right, go up m units
- m is the gradient
- If m is negative, go down
- If m is a fraction, remember that gradient is change in y divided by change in x
  - A gradient of $\frac{a}{b}$ would be $a$ units up for every $b$ units right
This creates a sequence of points which you can then join up
- Be careful of counting squares if axes have different scales
  - 1 unit might not be 1 square

What if the equation is not in the form y = mx + c?

Equations will not always be presented in the form y = mx + c
Rearranging to y = mx + c will make plotting these graphs easier
Consider the equation $3 x + 5 y = 30$
- Subtract 3x from both sides
  - $5 y = - 3 x + 30$
- Divide both sides by 5
  - $y = - \frac{3}{5} x + 6$
- It can now be seen that the gradient is $- \frac{3}{5}$ and the y-intercept is 6
Make sure you only have 1 y on one side, rather than say, 5y

How can I plot equations in the form ax + by = c?

Instead of rearranging, equations in the form ax + by = c, like the example above, can also be plotted by considering the x and y intercepts instead
- Substitute in x = 0 to find the y-intercept
- Substitute in y = 0 to find the x-intercept
- E.g. for $3 x + 5 y = 30$
  - When $x = 0$ , $5 y = 30$ , so $y = 6$
  - When $y = 0$ , $3 x = 30$ , so $x = 10$
- The points (0, 6) and (10, 0) can then be plotted and joined with a straight line

Examiner Tips and Tricks

Always plot at least 3 points (just in case one of your end points is wrong!)

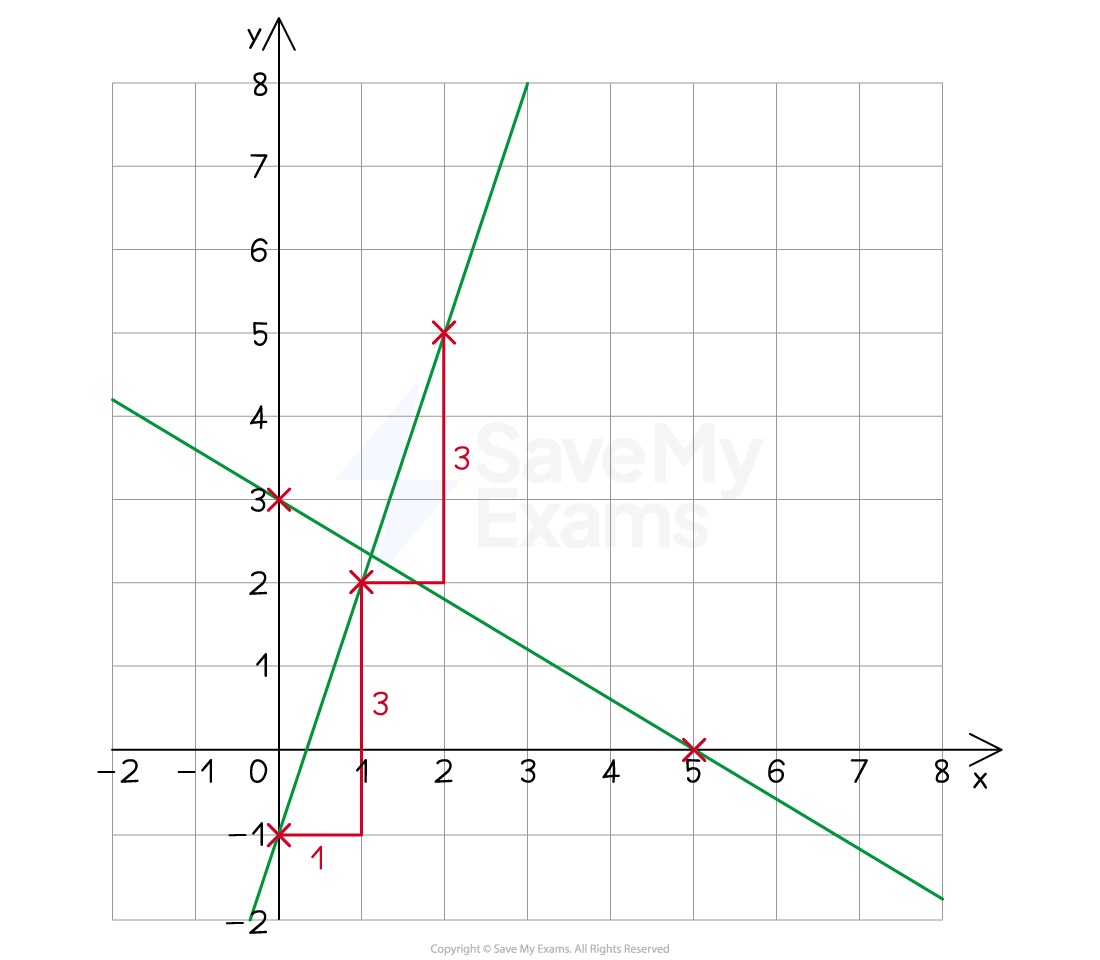
Worked Example

On the same set of axes, draw the graphs of $\frac{y + 1}{3} = x$ and $y = - \frac{3}{5} x + 3$ .

Rearrange $\frac{y + 1}{3} = x$ into the form $y = m x + c$ to make it easier to plot

$\begin{array}{rcl} \frac{y + 1}{3} & = & x \\ y + 1 & = & 3 x \\ y & = & 3 x - 1 \end{array}$

For $y = 3 x - 1$ , create a table of values

$x$	0	1	2
$y$	-1	2	5

Plot the points (0, -1), (1, 2) and (2, 5)
Connect with a straight line

Alternatively, start at the y-intercept (0, -1) and mark the next points 3 units up for every 1 unit to the right

For $y = - \frac{3}{5} x + 3$ , create a table of values
Because of the fraction, x = 5 is a good point to include

$x$	0	3	5
$y$	3	1.2	0

Plot the points (0, 3), (3, 1.2) and (5, 0)
Connect with a straight line

Alternatively, start at the y-intercept (0, 3) and mark the next points 3 units down for every 5 units to the right

Plotting the straight lines y=3x-1 and y=(-3/5)x+3 on the same axes

Last updated: 17 October 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Equations of Straight Lines (y = mx + c)Next:Parallel Lines