AP®MathsCollege BoardCalculus ABExam QuestionsUnit 8: Applications of IntegrationVolumes of Revolution

Volumes of Revolution (College Board AP® Calculus AB): Exam Questions

1 hour30 questions

Select a download format for Volumes of Revolution

Scroll for more

Select an answer set to view for
Volumes of Revolution

Easy
Medium
Hard
1
Sme Calculator
1 mark

Let R be the region in the first and second quadrants bounded above by the curve of y equals negative x squared plus 3 x plus 10 and below by the x-axis.

What limits of integration are required when the region R is rotated about the x-axis to generate a solid?

How did you do?

2
Sme Calculator
4 marks
Graph showing the region R that is bounded above by y=3x^2, below by the x-axis and to the right by the line y=5.

Let R be the region in the first quadrant bounded by the graph of y equals 3 x squared, the x-axis and the line x equals 5 as shown in the figure above.

Find the volume of the solid generated when R is rotated about the x-axis.

How did you do?

3
Sme Calculator
3 marks
Graph showing the function y = square root (3x - 4). The area bounded by the function, the line y=5, and the coordinate axes is shaded and labeled R.

Let R be the region in the first quadrant enclosed by the graph of y equals square root of 3 x minus 4 end root, the line y equals 5, and the coordinate axes as shown in the figure above.

Write, but do not evaluate, an integral expression for the volume of the solid generated when R is rotated about the y-axis.

How did you do?

4
Sme Calculator
4 marks
Graph of the functions y=x^2-2x+2 and y=2. The region bound by both functions is labeled R. The points of intersection of the two functions are labeled (0, 2) and (2, 2).

Let R be the region enclosed by the graph of f open parentheses x close parentheses equals x squared minus 2 x plus 2 and the horizontal line y equals 2, as shown in the figure above.

Find the volume of the solid generated when R is rotated about the horizontal line y equals 2.

How did you do?

5
Sme Calculator
3 marks
Graph showing the function y = square root(x) + 3, and the lines y = 3 and x = 4. The region enclosed by the curve and two lines is shaded and labeled R.

Let R be the region enclosed by the curve y equals square root of x plus 3, the line y equals 3, and the line x equals 4 as shown in the figure above.

Show that the volume of the solid generated by rotating the region R about the line x equals 4 can be found by evaluating the integral V equals pi space integral subscript 3 superscript 5 space open parentheses open parentheses y minus a close parentheses squared minus b close parentheses squared space d y where a and b are constants to be found.

How did you do?

1
Sme Calculator
3 marks
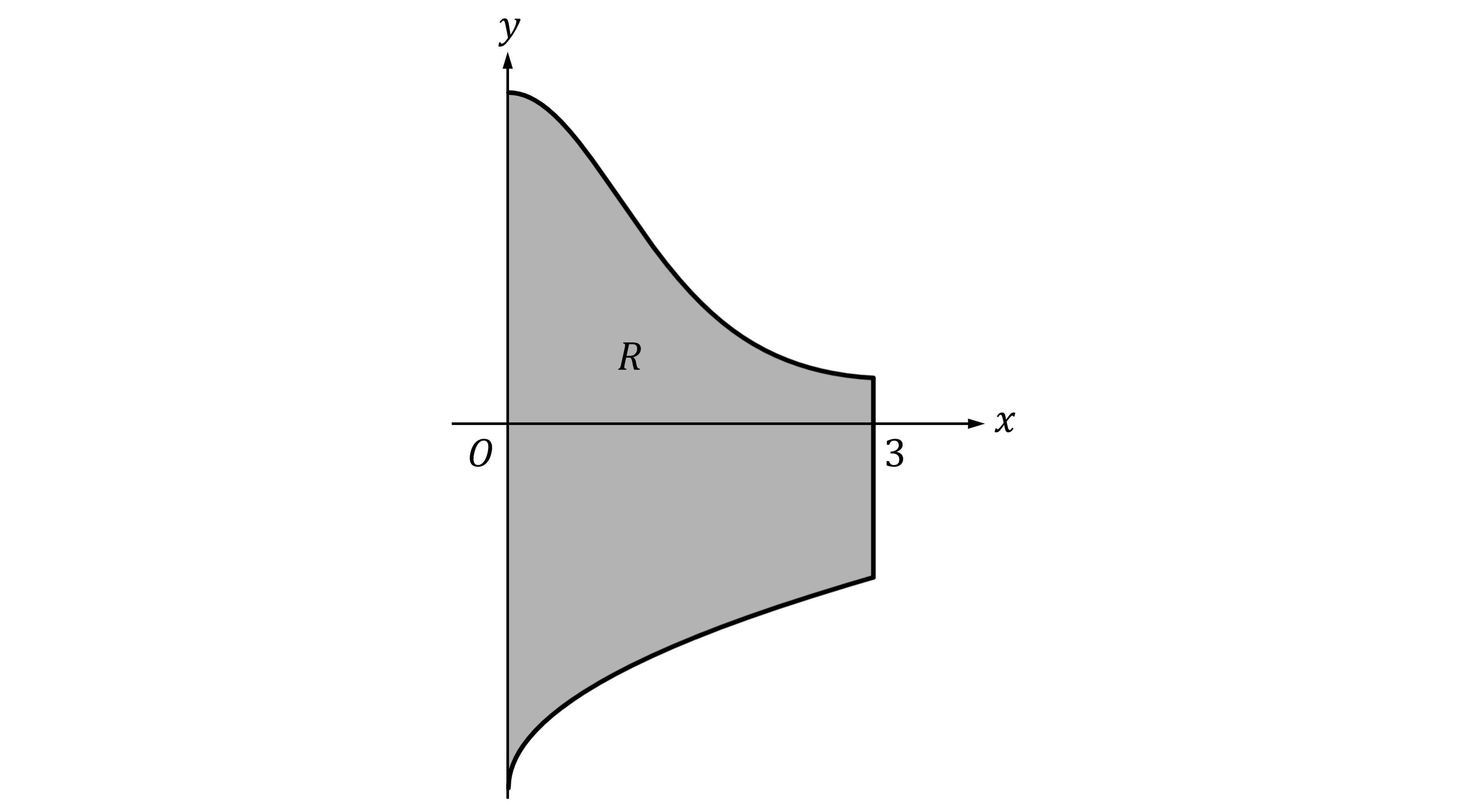
Graph showing the shaded region R bounded by the y-axis, the line x=3, and the curves y=e^cosx and y=sqrt(x)-3

Let R be the region enclosed by the graphs of f open parentheses x close parentheses equals e to the power of cos x end exponent and g open parentheses x close parentheses equals square root of x minus 3, the y-axis, and the vertical line x equals 3, as shown in the figure above.

Write, but do not evaluate, an integral expression that gives the volume of the solid generated when R is rotated about the horizontal line y equals 3.

How did you do?

2
Sme Calculator
4 marks
Graph showing the shaded region R in the first quadrant bounded by the positive coordinate axes and the curve y=((x-2)/2)^2

Let R be the region in the first quadrant enclosed by the coordinate axes and the graph of y equals open parentheses fraction numerator x minus 2 over denominator 2 end fraction close parentheses squared, as shown in the figure above.

Find the volume of the solid generated when R is rotated about the x-axis.

How did you do?

3
Sme Calculator
3 marks
Illustration of vase with a circular base and a smaller circular top. A circular cross-section of the vase is labeled with its radius, r, and the vertical height, h, from the base.

The inside of a vase of height 10 inches has circular cross sections, as shown in the figure above. At height h from the bottom of the vase, the radius of the vase is given by r equals 1 over 20 open parentheses 8 plus h squared close parentheses, where 0 less or equal than h less or equal than 10. The units of r and h are in inches.

Find the volume of the vase.

How did you do?

4
Sme Calculator
3 marks

Let R be the region in the first and second quadrants bounded above by the curve of y equals fraction numerator 99 over denominator 1 plus 2 x squared end fraction and below by the horizontal line y equals 3.

Find the volume of the solid generated when R is rotated about the x-axis.

How did you do?

5
Sme Calculator
3 marks
Graph of two functions on the interval 0<=x<=2. The functions intersect at (, 0) and (2, 3). The region bounded by the two functions is labeled R.

Let R be the region in the first quadrant enclosed by the graphs f open parentheses x close parentheses equals 3 over 4 x squared and g open parentheses x close parentheses equals 3 space sin space open parentheses fraction numerator pi x over denominator 4 end fraction close parentheses on the interval 0 less or equal than x less or equal than 2 as shown in the figure above.

Write, but do not evaluate, an integral expression for the volume of the solid generated when R is rotated about the vertical line x equals 2.

How did you do?

1
Sme Calculator
4 marks
A graph of the curve with equation x^2=(ky)^2*(9-y^2) for x>0, y>0

A company designs fishing lures using the family of curves with equation open parentheses k y close parentheses squared open parentheses 9 minus y squared close parentheses minus x squared equals 0, where k is a positive constant. The figure above shows the region in the first quadrant bounded by the y-axis and the curve open parentheses k y close parentheses squared open parentheses 9 minus y squared close parentheses minus x squared equals 0, for some k. Each fishing lure is in the shape of the solid generated when such a region is revolved about the y-axis. Both x and y are measured in inches.

For a particular fishing lure, the volume is fraction numerator 162 pi over denominator 25 end fraction cubic inches. What is the value of k for this fishing lure?

How did you do?

2
Sme Calculator
3 marks
Graph of the shaded region R bounded by the y-axis and the curves y=sec(1-x) and y=x^3/8

Let R be the region in the first quadrant enclosed by the y-axis, the line x equals 2, and the graphs of y equals sec open parentheses 1 minus x close parentheses and y equals x cubed over 8, as shown in the figure above.

Find the volume of the solid generated when R is rotated about the x-axis.

How did you do?

3
Sme Calculator
4 marks
Graph of the shaded region R bounded by the coordinate axes, the line y=8, and the curves with equations y=x^2+1 and y=(x-4)^3

Let R be the region in the first quadrant enclosed by the coordinate axes, the line y equals 8, and the graphs of y equals x squared plus 1 and y equals open parentheses x minus 4 close parentheses cubed, as shown in the figure above.

Find the volume of the solid generated when R is rotated about the y-axis.

How did you do?

4
Sme Calculator
4 marks

Let f open parentheses x close parentheses equals 1 half x cubed minus 4 and R be the region in the fourth quadrant bounded below by the graph y equals f open parentheses x close parentheses, above by the x-axis and to the left by the y-axis.

Find the volume of the solid generated when R is rotated about the horizontal line y equals negative 6.

How did you do?

5
Sme Calculator
5 marks
Graph of functions f and g. The area bound on the left by the y-axis, above by f(x) and below by g(x) is shaded and labeled R. The functions then intersect. The area bounded above by g(x) and below by f(x) is shaded and labeled S. The functions then intersect again.

Let f and g be the functions given by f left parenthesis x right parenthesis equals 3 over 2 plus cos open parentheses 2 pi x close parentheses and g left parenthesis x right parenthesis equals ln space open parentheses x plus 2 close parentheses. Let R be the shaded region in the first quadrant enclosed by the y-axis and the graphs of f and g, and let S be the shaded region in the first quadrant enclosed by the graphs of f and g as shown in the figure above.

Find the volume of the solid generated when R and S are revolved around the horizontal line y equals negative 1.

How did you do?