Interference & Coherence (Cambridge (CIE) A Level Physics)

Interference & coherence

Interference

• Interference occurs when waves overlap and their resultant displacement is the sum of the displacement of each wave

• This result is based on the principle of superposition and the resultant waves may be smaller or larger than either of the two individual waves

• Interference of two waves can either be:

  • In phase, causing constructive interference. The peaks and troughs line up on both waves. The resultant wave has double the amplitude

  • In anti-phase, causing destructive interference. The peaks on one wave line up with the troughs of the other. The resultant wave has no amplitude

Constructive and destructive interference

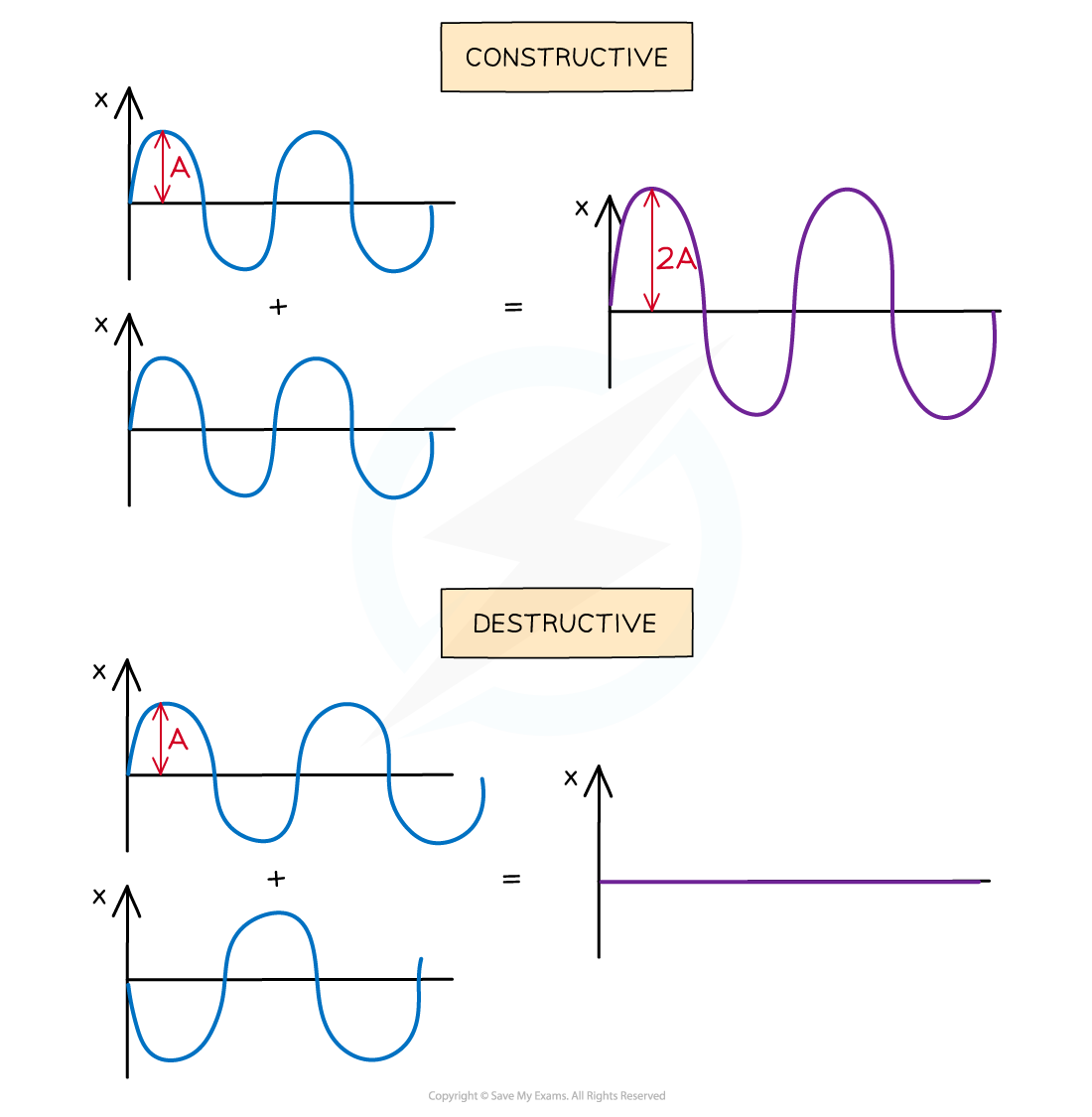
Waves in superposition can undergo constructive or destructive interference

Conditions for constructive and destructive interference

• In general, for waves emitted by two coherent sources very close together:

• The condition for constructive interference is:

path difference = 

• The condition for destructive interference is:

path difference = 

• Where:

  • λ = wavelength of the waves in metres (m)

  • n = 0, 1, 2, 3... (any other integer)

 Coherence

• At points where the two waves are neither in phase nor in antiphase, the resultant amplitude is somewhere in between the two extremes

• Waves are coherent if they have the same frequency and constant phase difference

Coherent vs. incoherent waves

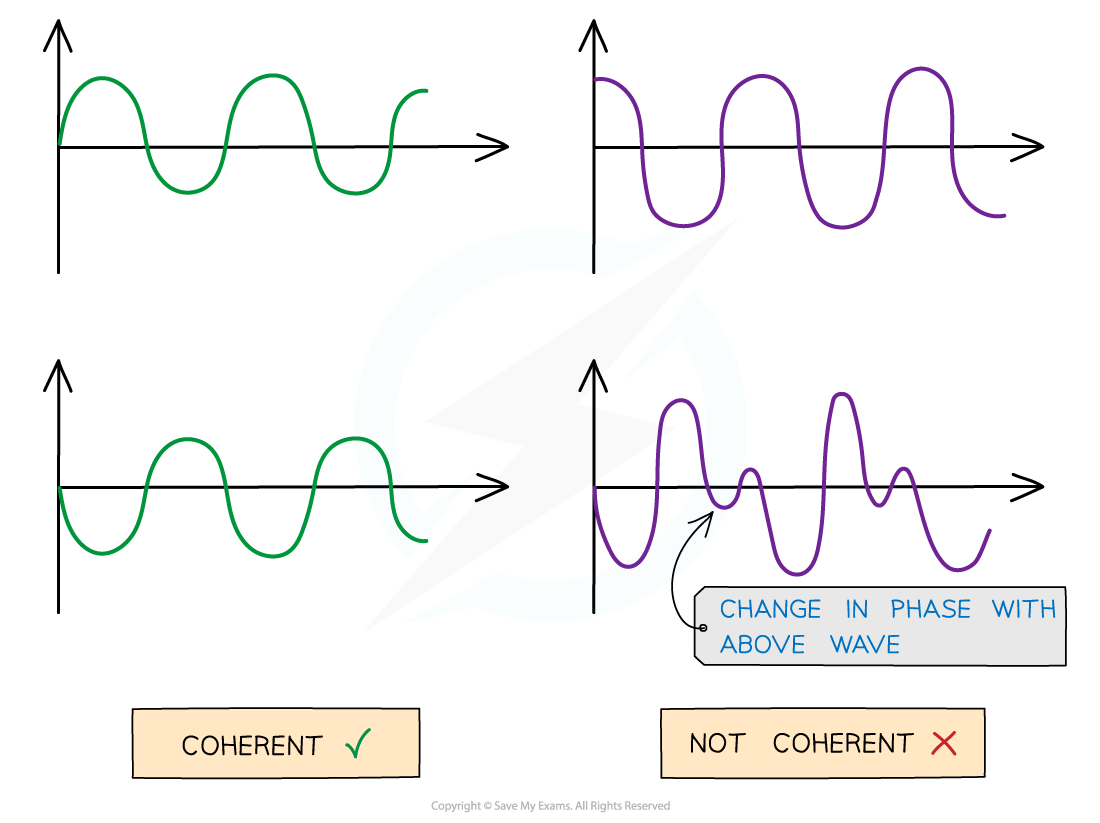
Coherent v non-coherent wave. The abrupt change in phase creates an inconsistent phase difference

• Coherence is vital in order to produce an observable interference pattern

• Laser light is an example of a coherent light source, whereas filament lamps produce incoherent light waves