Half-Life (Cambridge (CIE) O Level Physics): Revision Note

Half-Life Basics

• It is impossible to know when a particular unstable nucleus will decay

• But the rate at which the activity of a sample decreases can be known

  • This is known as the half-life

• Half-life is defined as:

  The time taken for half the nuclei of that isotope in any sample to decay

• In other words, the time it takes for the activity of a sample to fall to half its original level

• Different isotopes have different half-lives and half-lives can vary from a fraction of a second to billions of years in length

• Half-life can be determined from an activity–time graph

How to Determine Half-Life

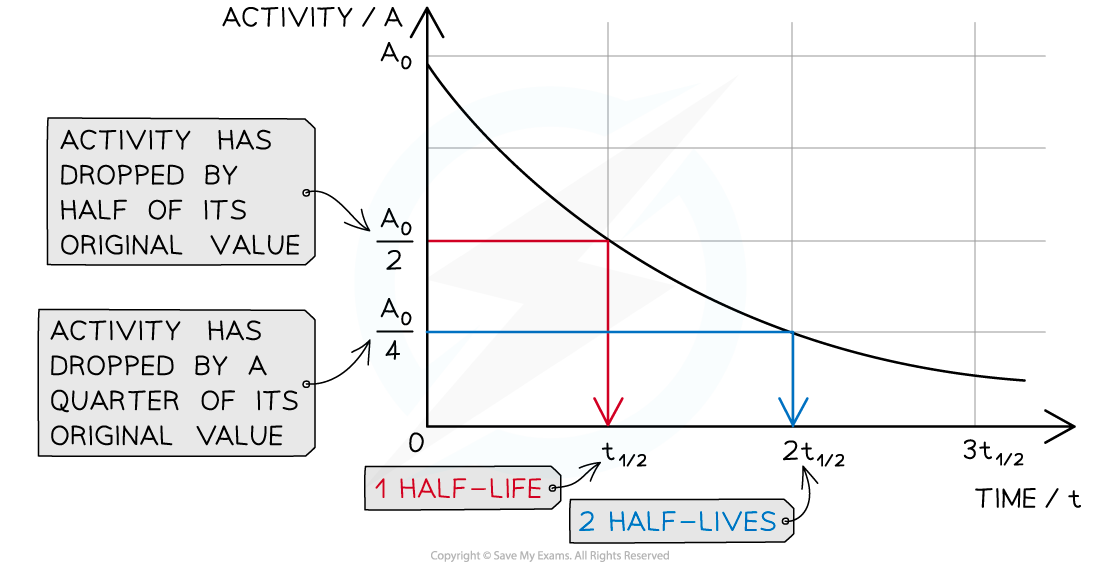
The graph shows how the activity of a radioactive sample changes over time. Each time the original activity halves, another half-life has passed

• The time it takes for the activity of the sample to decrease from 100 % to 50 % is the half-life

  • It is the same length of time as it would take to decrease from 50 % activity to 25 % activity

  • The half-life is constant for a particular isotope

• The table below shows that

  • As the number of half-lives increases by 1, the proportion of the isotope remaining halves

Relationship between the number of half-lives to the proportion of isotope remaining

Dating of Objects Using C-14

• The isotope carbon-14 is commonly used in radioactive dating due to its abundance in living tissue

• Carbon-14 forms when a high-energy cosmic ray knocks a neutron out of a nucleus, which then collides with a nitrogen nucleus in the air

• This process can be represented by the equation:

• Plants take in carbon dioxide from the atmosphere for photosynthesis, including the radioactive isotope carbon-14

• Animals and humans take in carbon-14 by eating the plants

  • Therefore, all living organisms absorb carbon-14, but after they die they do not absorb any more

• The proportion of carbon-14 is constant in living organisms as carbon is constantly being replaced during the period they are alive

• When an organism dies, the activity of carbon-14 in the organic matter starts to fall, with a half-life of around 5730 years

• Samples of living material can be tested by measuring the current amount of carbon-14 it contains and comparing this to the initial amount (which is based on the current ratio of carbon-14 to carbon-12)

  • The proportion of carbon-14 a sample contains can therefore provide an approximate age for the sample 

Reliability of Carbon Dating

• Carbon dating is a highly reliable ageing method for samples ranging from around 1000 to 40 000 years old

  • Therefore, for very young, or very old samples, carbon dating is not the most reliable method to use

• This can be explained by looking at the decay curve of carbon-14:

Decay Curve for Carbon-14

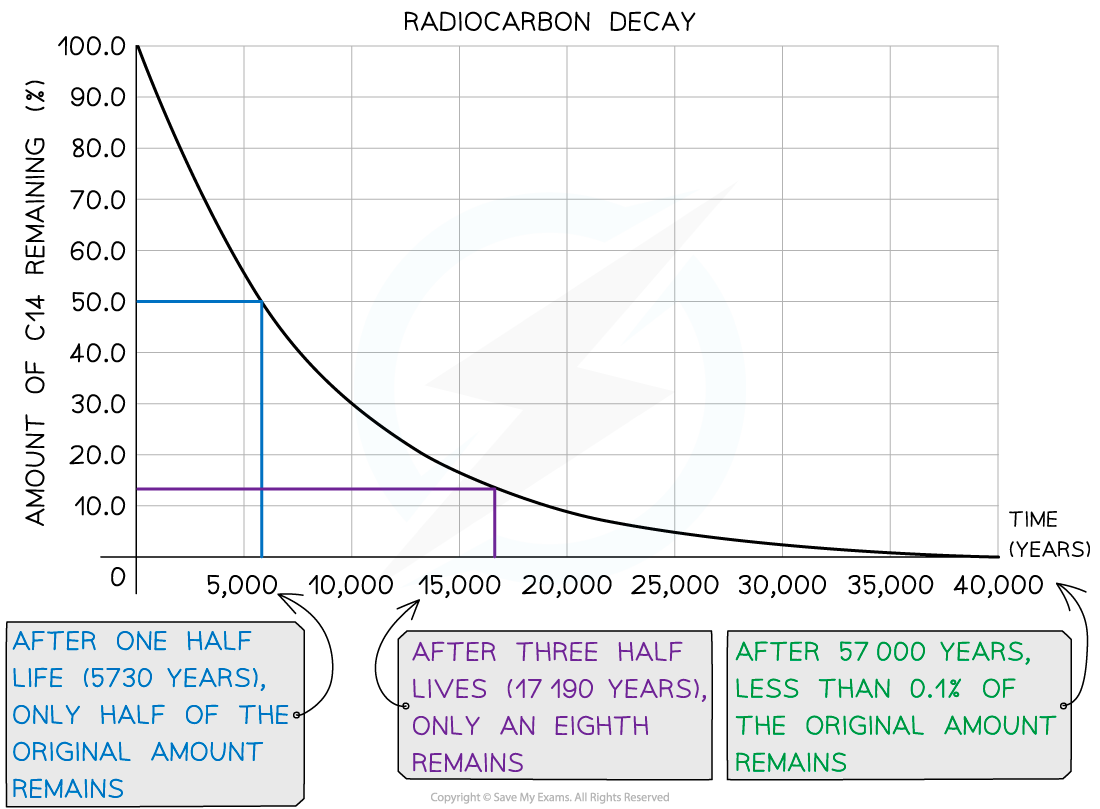
Carbon-14 decay curve used for carbon dating

• If the sample is less than 1000 years old:

  • The activity of the sample will be too high

  • So, it is difficult to accurately measure the small change in activity

  • Therefore, the ratio of carbon-14 to carbon-12 will be too high to determine an accurate age

• If the sample is more than 40 000 years old:

  • The activity will be too small and have a count rate similar to that of background radiation

  • So, there will be very few carbon-14 atoms remaining, hence very few decays will occur

  • Therefore, the ratio of carbon-14 to carbon-12 will be too small to determine an accurate age

• Carbon dating uses the currently known ratio of carbon-14 to carbon-12, however, scientists cannot know the level of carbon-14 in the biosphere thousands of years ago

• Therefore, this makes it difficult to age samples which are very old