Fission & Fusion (Cambridge (CIE) O Level Physics): Revision Note

Fission & Fusion

• Nuclei can join together, or split up, to form new nuclei

• These processes are known are

  • Nuclear fission

  • Nuclear fusion

Nuclear Fission

• There is a lot of energy stored within the nucleus of an atom

  • This energy can be released in a nuclear reaction such as fission

• Nuclear fission is defined as:

The splitting of a large, unstable nucleus into two smaller nuclei

• Isotopes of uranium and plutonium both undergo fission and are used as fuels in nuclear power stations

• During fission, when a neutron collides with an unstable nucleus, the nucleus splits into two smaller nuclei (called daughter nuclei) as well as two or three neutrons

  • Gamma rays are also emitted

How does nuclear fission work?

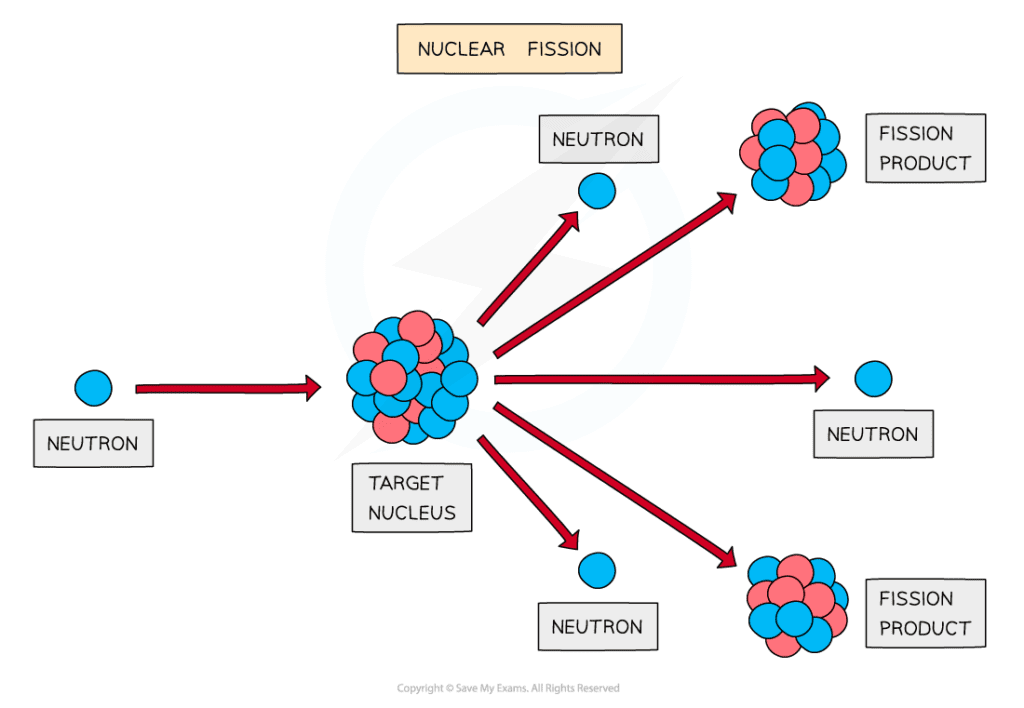
A neutron is fired into the target nucleus, causing it to split into two smaller nuclei

• The products of fission move away very quickly

  • Energy transferred is from nuclear potential energy to kinetic energy

• The mass of the products (daughter nuclei and neutrons) is less than the mass of the original nucleus

  • This is because the remaining mass has been converted into energy which is released during the fission process

Nuclear Fusion

• Small nuclei can react to release energy in a process called nuclear fusion

• Nuclear fusion is defined as:

When two light nuclei join to form a heavier nucleus

• This process requires extremely high temperatures to maintain

  • This is why nuclear fusion has proven very hard to reproduce on Earth

• Stars use nuclear fusion to produce energy

• In most stars, hydrogen atoms are fused together to form helium and produce lots of energy

How does nuclear fusion work?

Two hydrogen nuclei are fusing to form a helium nuclei

• The energy produced during nuclear fusion comes from a very small amount of the particle’s mass being converted into energy

• Albert Einstein described the mass-energy equivalence with his famous equation:

• Where:

  • E = energy released from fusion in Joules (J)

  • m = mass converted into energy in kilograms (kg)

  • c = the speed of light in metres per second (m/s)

• Therefore, the mass of the product (fused nucleus) is less than the mass of the two original nuclei

  • This is because the remaining mass has been converted into energy which is released when the nuclei fuse

• The amount of energy released during nuclear fusion is huge:

  • The energy from 1 kg of hydrogen that undergoes fusion is equivalent to the energy from burning about 10 million kilograms of coal

• An example of a nuclide equation for fusion is:

+ energy

• Where:

  • is deuterium (isotope of hydrogen with 1 proton and 1 neutron)

  • is hydrogen (with one proton)

  • is an isotope with helium (with two protons and one neutron)

Fission Reactions

• The processes involved in nuclear fission can be shown in different ways, such as diagrams and nuclear equations

Fission of Uranium-235

Large nuclei can decay by fission to produce smaller nuclei and neutrons with a lot of kinetic energy

• The diagram above is useful because it shows clearly the different parts of the fission reaction

• An example of a nuclide equation for fission is:

energy

• Where:

  • is an unstable isotope of Uranium

  • is a neutron

  • us an unstable isotope of Krypton

  • is an unstable isotope of Barium

• This equation represents a fission reaction in which

  • A Uranium-235 nucleus is hit by a neutron

  • It splits into two smaller nuclei – a Krypton nucleus and a Barium nucleus

  • Three neutrons are released in the process which can go on to trigger further fission reactions

• The sum of the top (nucleon) numbers on the left-hand side equals the sum of top number on the right-hand side:

235 + 1 = 92 + 141 + (3 × 1)

• The same is true for the lower (proton) numbers:

92 + 0 = 36 + 56 + (2 × 0)

Chain Reactions

• Only one extra neutron is required to induce a Uranium-235 nucleus to split by fission

• During the fission, it produces two or three neutrons which move away at high speed

• Each of these new neutrons can start another fission reaction, which again creates further excess neutrons

• This process is called a chain reaction

Chain Reaction Analogy

The neutrons released by each fission reaction can go on to create further fissions, like a chain that is linked several times – from each chain comes two more

Controlled Chain Reactions

• In a nuclear reactor, a chain reaction is required to keep the reactor running

• When the reactor is producing energy at the correct rate, the number of free neutrons in the reactor needs to be kept constant

  • This means some must be removed from the reactor

• To do this, nuclear reactors contain control rods

• These absorb neutrons without becoming dangerously unstable themselves

Uncontrolled Chain Reactions

• Because each new fission reaction releases energy, uncontrolled chain reactions can be dangerous

• The number of neutrons available increases quickly, so the number of reactions does too

• A nuclear weapon uses an uncontrolled chain reaction to release a huge amount of energy in a short period of time as an explosion

Nuclear Reactors

• In a nuclear reactor, a chain reaction is required to keep the reactor running

• When the reactor is producing energy at the required rate, two factors must be controlled:

  • The number of free neutrons in the reactor

  • The energy of the free neutrons

• The main components of a nuclear reactor are:

  • control rods

  • a moderator

Nuclear reactor diagram

The overall purpose of the reactor is to control chain reactions and collect the heat energy produced from nuclear reactions to generate electricity

Control rods

Purpose of control rods: To absorb neutrons

• Control rods are made of a material which absorbs neutrons without becoming dangerously unstable themselves

• The number of neutrons absorbed is controlled by varying the depth of the control rods in the reactor core

  • Lowering the rods further decreases the rate of fission, as more neutrons are absorbed

  • Raising the rods increases the rate of fission, as fewer neutrons are absorbed

• This is adjusted automatically so that exactly one fission neutron produced by each fission event goes on to cause another fission

• In the event the nuclear reactor needs to shut down, the control rods can be lowered all the way so no reactions can take place

Moderator

Purpose of a moderator: To slow down neutrons

• The moderator is a material that surrounds the fuel rods and control rods inside the reactor core

• The fast-moving neutrons produced by the fission reactions slow down by colliding with the molecules of the moderator, causing them to lose some momentum

• The neutrons are slowed down so that they are in thermal equilibrium with the moderator

  • These neutrons are called thermal neutrons

  • This ensures neutrons can react efficiently with the uranium fuel