Snell's Law

Refractive Index & Snell's Law

Refractive Index

The refractive index is a number which is related to the speed of light in the material (which is always less than the speed of light in a vacuum):
The refractive index is a number that is always larger than 1 and is different for different materials
- Objects which are more optically dense have a higher refractive index, eg. n is about 2.4 for diamond
- Objects which are less optically dense have a lower refractive index, eg. n is about 1.5 for glass

Since refractive index is a ratio, it has no units

When light enters a denser medium (such as glass) it slows down and bends towards the normal
- How much the light bends depends on the density of the material

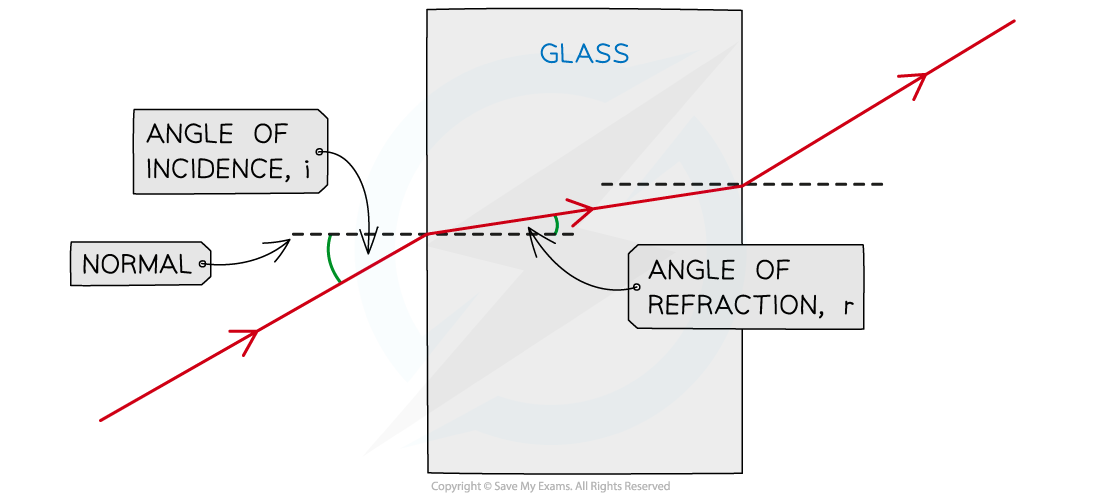
$Refraction of Light, downloadable IGCSE & GCSE Physics revision notes$

Angle of incidence i and angle of refraction r through a glass block

If light travels from a less dense to a more dense medium (e.g. air to glass), r < i (bends towards the normal)
If light travels from a more dense to a less dense medium (e.g. glass to air), r > i (bends away from the normal)

The angles of incidence and refraction are related by an equation known as Snell's Law:

$n = \frac{\sin i}{\sin r}$

Where:
- n = the refractive index of the material
- i = angle of incidence of the light (°)
- r = angle of refraction of the light (°)

'Sin' is the trigonometric function 'sine' which is on a scientific calculator

Worked example

A ray of light enters a glass block of refractive index 1.53 making an angle of 15° with the normal before entering the block.

Calculate the angle it makes with the normal after it enters the glass block.

Answer:

Step 1: List the known quantities

Refractive index of glass, n = 1.53
Angle of incidence, i = 15°

Step 2: Write the equation for Snell's Law

$n = \frac{\sin i}{\sin r}$

Step 3: Rearrange the equation and calculate sin (r)

$\sin r = \frac{\sin i}{n}$

$\sin r = \frac{\sin (15 °)}{1.53} = 0.1692$

Step 4: Find the angle of refraction (r) by using the inverse sin function

r = sin^–1 (0.1692) = 9.7 = 10°

Exam Tip

Important: (sin i / sin r) is not the same as (i / r). Incorrectly cancelling the sin terms is a very common mistake!

When calculating the value of i or r start by calculating the value of sin i or sin r.

You can then use the inverse sin function (sin^–1 on most calculators by pressing 'shift' then 'sine') to find the angle.

One way to remember which way around i and r are in the fraction is remembering that 'i' comes before 'r' in the alphabet, and therefore is on the top of the fraction (whilst r is on the bottom).

Additionally, make sure your calculator is in degrees mode, not radians mode, when you are given i and r in degrees.

Snell's Law (Cambridge O Level Physics)

Revision Note

Refractive Index & Snell's Law

Refractive Index

Snell's Law

Worked example

Exam Tip

You've read 0 of your 0 free revision notes

Get unlimited access

Join the 100,000+ Students that ❤️ Save My Exams

Author: Dan MG