Specific Heat Capacity (Cambridge (CIE) O Level Physics): Revision Note

Internal Energy

• A rise in the temperature of an object increases its internal energy

  • This can be thought of as due to an increase in the average speed of the particles

  • Increasing speed increases kinetic energy

• Internal energy is defined as:

  The total energy stored inside a system by the particles that make up the system due to their motion and positions

  • Motion of the particles affects their kinetic energy

  • Positions of the particles relative to each other affects their potential energy

• Together, these two make up the internal energy of the system

Substances have internal energy due to the motion of the particles and their positions relative to each other

Average Kinetic Energy

• Heating a system will change the energy stored in a system by increasing the kinetic energy of its particles

  • The Kelvin temperature of the gas is related to the average kinetic energy of the molecules

• This increase in kinetic energy (and therefore energy stored in the system) can:

  • Cause the temperature of the system to increase

  • Or, produce a change of state (solid to liquid or liquid to gas)

• The internal energy of a gas is the sum of the kinetic energy of all the molecules

• The higher the temperature, the higher the average kinetic energy of the molecules and vice versa

  • This means they move faster

  • This applies to all states of matter, but the motion of particles in a solid is different to that of particles in a gas

• If the temperature of a gas is increased, the particles move faster and gain kinetic energy

  • Therefore, they will collide more with each other and the container leading to an increase in pressure

• The temperature (in Kelvin) is proportional to the average kinetic energy of the molecules

T ∝ KE

Specific Heat Capacity

• How much the temperature of a system increases depends on:

  • The mass of the substance heated

  • The type of material

  • The amount of thermal energy transferred in to the system

• The specific heat capacity, c, of a substance is defined as:

  The amount of energy required to raise the temperature of 1 kg of the substance by 1 °C

• Different substances have different specific heat capacities

  • If a substance has a low specific heat capacity, it heats up and cools down quickly (ie. it takes less energy to change its temperature)

  • If a substance has a high specific heat capacity, it heats up and cools down slowly (ie. it takes more energy to change its temperature)

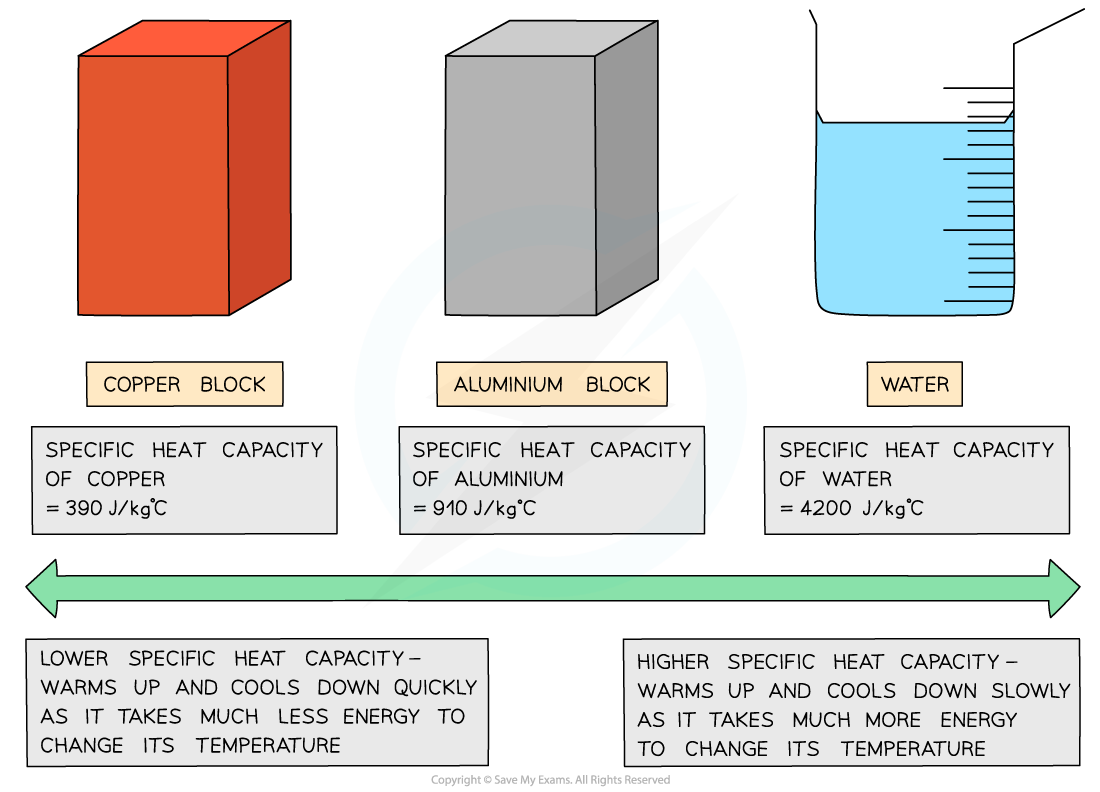
Low vs high specific heat capacity

Calculating Specific Heat Capacity

• The specific heat capacity in terms of the amount of energy needed to raise the temperature of a given mass by a given amount can be calculated using the equation:

• Where:

  • ΔE = change in thermal energy, in joules (J)

  • m = mass, in kilograms (kg)

  • c = specific heat capacity, in joules per kilogram per degree Celsius (J/kg °C)

  • Δθ = change in temperature, in degrees Celsius (°C)