Equilibrium (Cambridge (CIE) O Level Physics): Revision Note
Exam code: 5054
Did this video help you?
The Principle of Moments
The term equilibrium means that an object keeps doing what it’s doing, without any change
Therefore:
If the object is moving it will continue to move (in a straight line)
If it is stationary it will remain stationary
The object will also not start or stop turning
The above conditions require two things:
The forces on the object must be balanced
There must be no resultant force
The sum of clockwise moments on the object must equal the sum of anticlockwise moments
there must be no resultant moment
A Moving Car and a Balanced Beam in Equilibrium

When the forces and moments on an object are balanced, the object will remain in equilibrium
If the above two conditions are met, then the object will be in equilibrium
The Principle of Moments
The principle of moments states that:
If an object is balanced, the total clockwise moment about a pivot equals the total anticlockwise moment about that pivot
Remember that the moment = force × distance from a pivot
The forces should be perpendicular to the distance from the pivot
For example, on a horizontal beam, the forces which will cause a moment are those directed upwards or downwards
Worked Example
A parent and child are at opposite ends of a playground see-saw. The parent weighs 690 N and the child weighs 140 N. The adult sits 0.3 m from the pivot.
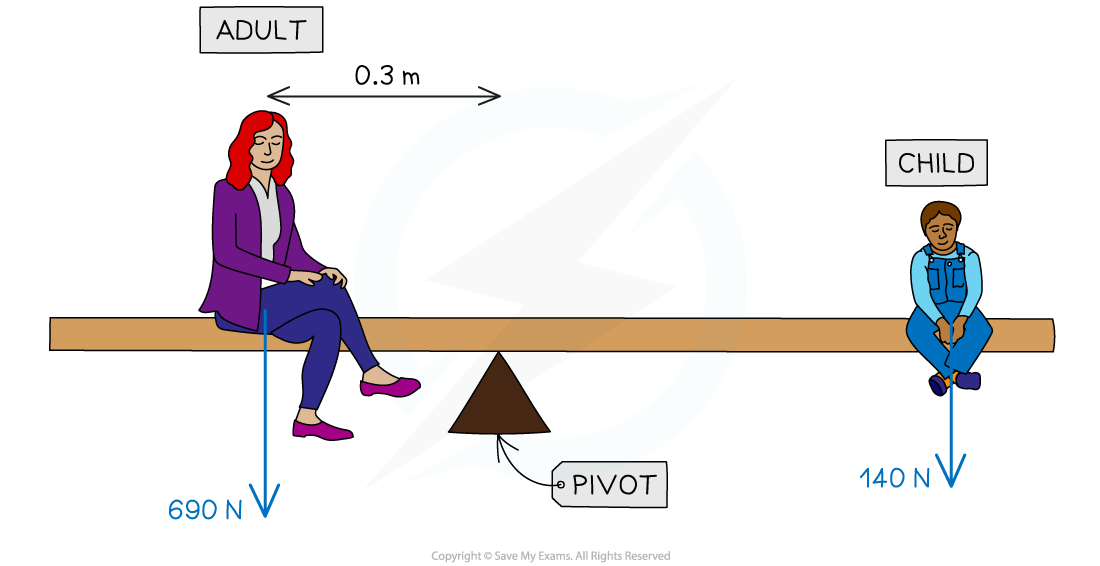
Calculate the distance the child must sit from the pivot for the see-saw to be balanced.
Answer:
Step 1: List the know quantities
Clockwise force (child), Fchild = 140 N
Anticlockwise force (adult), Fadult = 690 N
Distance of adult from the pivot, dadult = 0.3 m
Step 2: Write down the relevant equation
Moments are calculated using:
Moment = force × distance from pivot
For the see-saw to balance, the principle of moments states that
Total clockwise moments = Total anticlockwise moments
Step 3: Calculate the total clockwise moments
The clockwise moment is from the child
Momentchild = Fchild × dchild = 140 × dchild
Step 4: Calculate the total anticlockwise moments
The anticlockwise moment is from the adult
Momentadult = Fadult × dadult = 690 × 0.3 = 207 Nm
Step 5: Substitute into the principle of moments equation
140 × dchild = 207
Step 6: Rearrange for the distance of the child from the pivot
dchild = 207 ÷ 140 = 1.48 m
Examiner Tips and Tricks
Make sure that all the distances are in the same units and you’re considering the correct forces as clockwise or anticlockwise, as seen in the diagram below
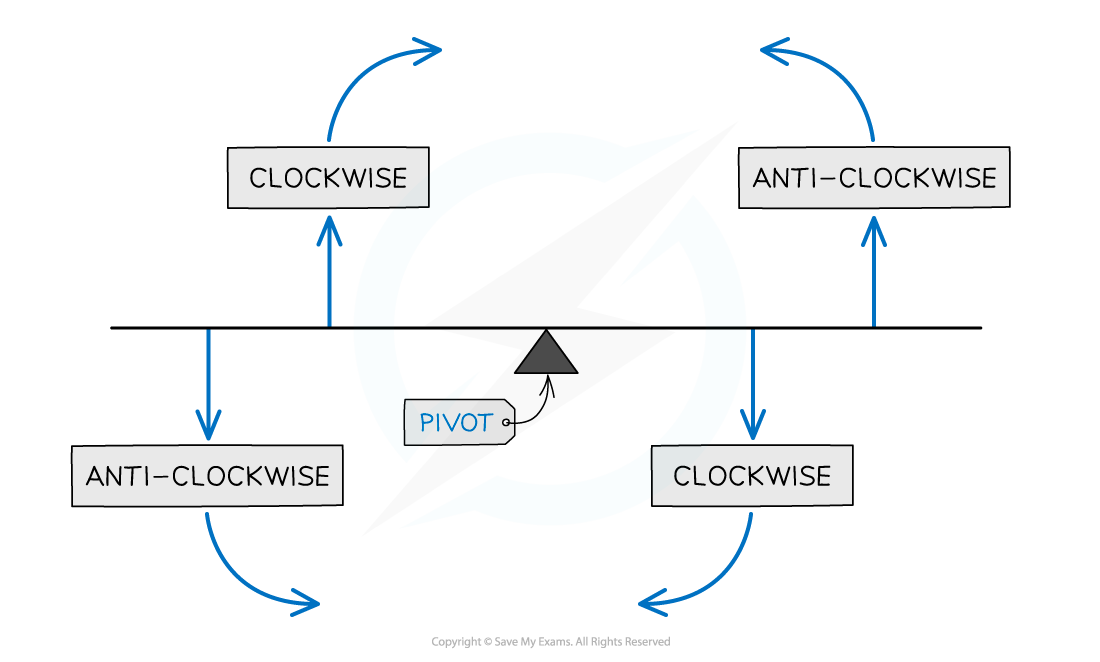
Clockwise is defined as the direction the hands of a clock move (and anticlockwise as the opposite)
Demonstrating Equilibrium
A simple experiment to demonstrate that there is no net moment on an object in equilibrium involves taking an object, such as a beam, and replacing the supports with newton (force) meters:
Forces on a Beam

Several forces act on a supported beam, including the mass of the beam and the mass of an object suspended from it
The beam in the above diagram is in equilibrium
The various forces acting on the beam can be found either by taking readings from the newton meters or by measuring the masses (and hence calculating the weights) of the beam and the mass suspended from the beam
The distance of each force from the end of the ruler can then be measured, allowing the moment of each force about the end of the ruler to be calculated
It can then be shown that the sum of clockwise moments (due to forces F2 and F3) equal the sum of anticlockwise moments (due to forces F1 and F4)
More detail on setting up this experiment
Use a meter ruler for the beam
Suspend it via two Newton meters, one on each side, that each hang from a clamp stand
F1 is the reading given on the left side Newton meter and F4 is the reading given on the right
Create a loop of string, tie a tight knot and slide the ruler through it
F3 will be the weight of a mass hook with 10 N weights suspended from this string
F2 is the weight of the beam

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?