Calculating with Vectors (Cambridge (CIE) O Level Physics) : Revision Note
Did this video help you?
Calculations with Vectors
Vectors are represented by an arrow
The arrowhead indicates the direction of the vector
The length of the arrow represents the magnitude

The two force vectors acting on the object have both a direction and a magnitude
Component vectors are sometimes drawn with a dotted line and a subscript indicating horizontal or vertical
For example, Fv is the vertical component of the force F
Calculating Vectors Graphically
Vectors at right angles to one another can be combined into one resultant vector
The resultant vector will have the same effect as the two original ones
To calculate vectors graphically means carefully producing a scale drawing with all lengths and angles correct
This should be done using a sharp pencil, ruler and protractor
Follow these steps to carry out calculations with vectors on graphs
Choose a scale which fits the page
For example, use 1 cm = 10 m or 1 cm = 1 N, so that the diagram is around 10 cm high
Draw the vectors at right angles to one another
Complete the rectangle
Draw the resultant vector diagonally from the origin
Carefully measure the length of the resultant vector
Use the scale factor to calculate the magnitude
Use the protractor to measure the angle
Vector drawn to scale
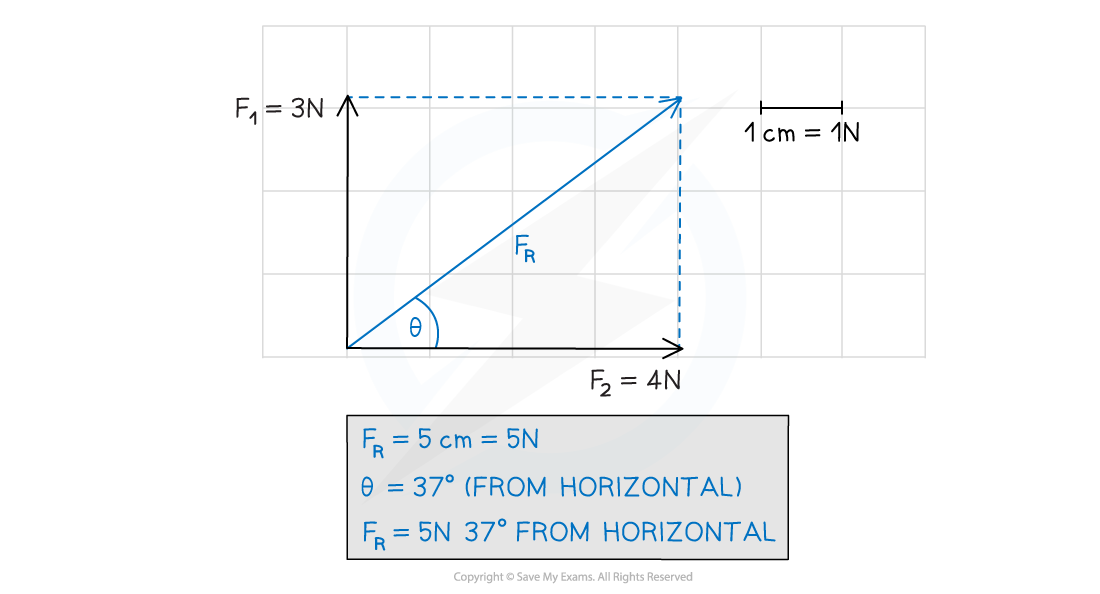
Vectors can be measured or calculated graphically if you are confident in using scales
Combining Vectors by Calculation
In this method, a diagram is still essential but it does not need to be exactly to scale
The diagram can take the form of a sketch, as long as the resultant, component and sides are clearly labelled
Resolving vectors

Resolving two force vectors F1 and F2 into a resultant force vector FR
Resultant vector

Use Pythagoras' Theorem to find the resultant vector
Pythagoras' Theorem

Pythagoras's Theorem makes calculating vectors at right angles much simpler
Use trigonometry to find the angle
The mnemonic 'soh-cah-toa' is used to remember how to apply sines and cosines to resolve the sides of a triangle
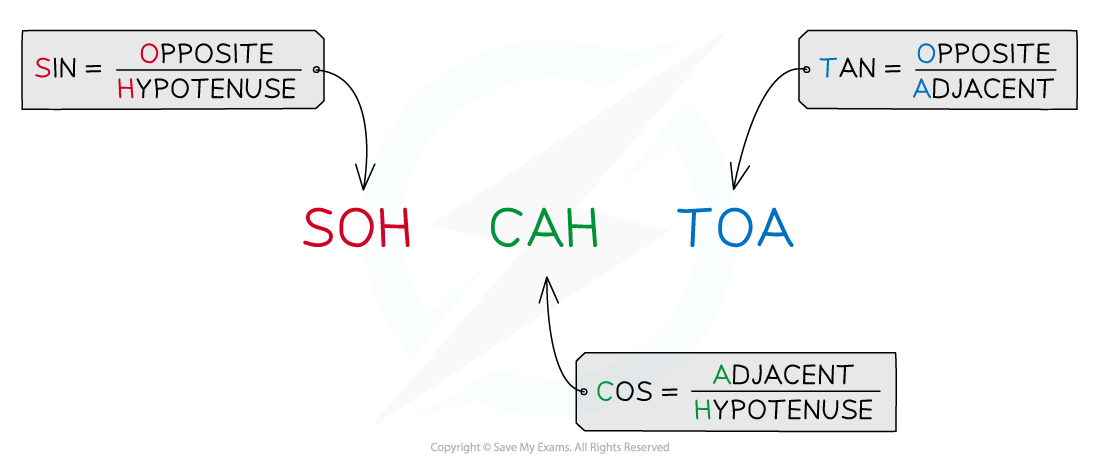

Trigonometry and Pythagoras' Therom are essential in vector calculations
Worked Example
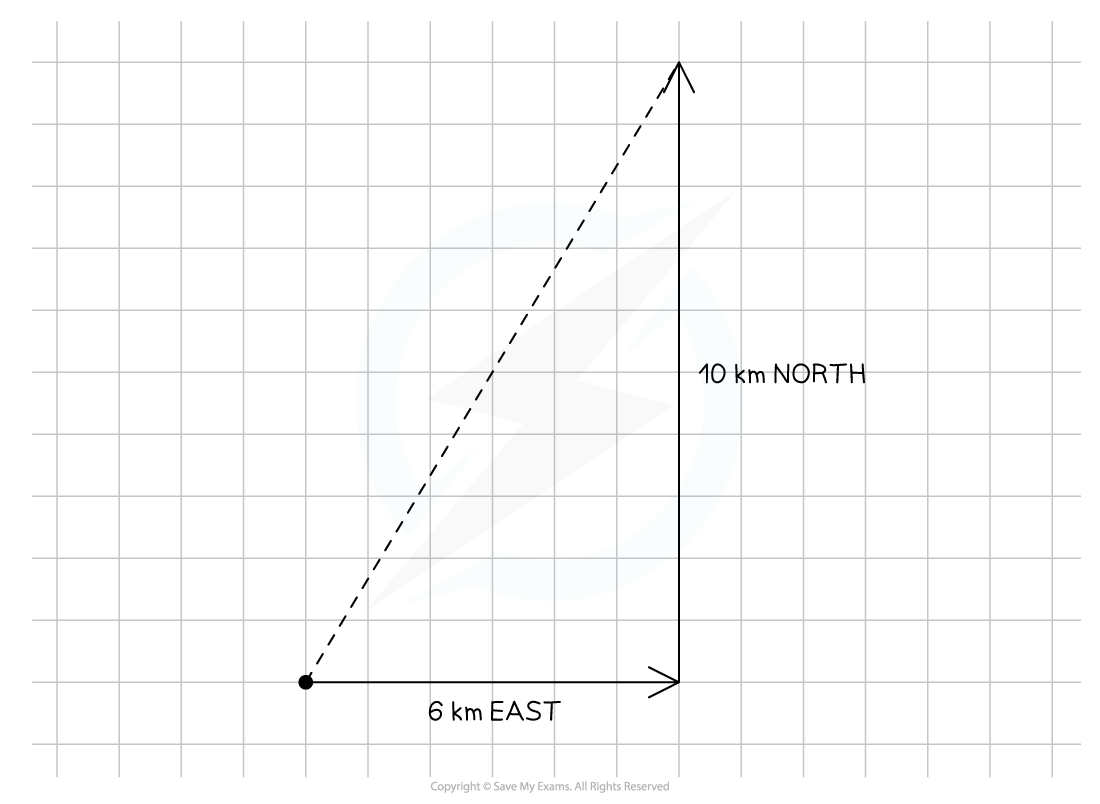
A hiker walks a distance of 6 km due east and 10 km due north.
Calculate the magnitude of their displacement and its direction from the horizontal.
Answer:
Step 1: Draw a vector diagram
Step 2: Calculate the magnitude of the resultant vector using Pythagoras' Theorem
Resultant vector = 11.66
Step 3: Calculate the direction of the resultant vector using trigonometry
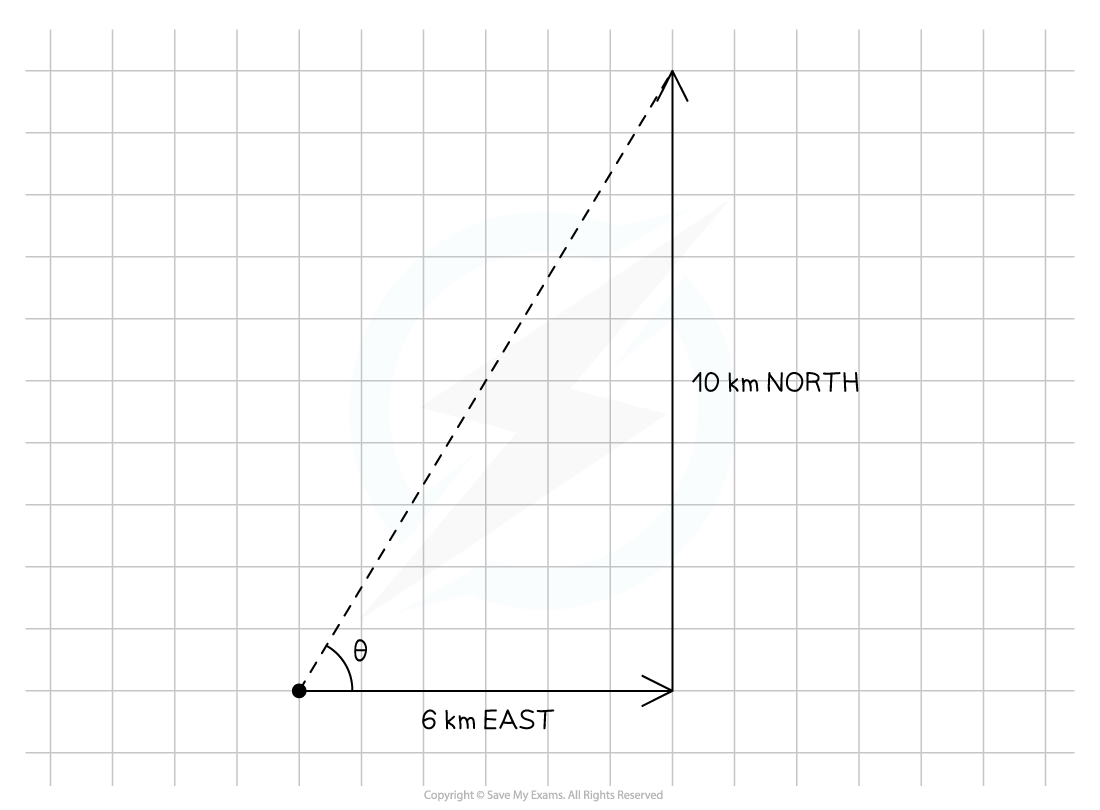
Step 4: State the final answer complete with direction
Resultant vector = 12 km 59° east and upwards from the horizontal
Examiner Tips and Tricks
If the question specifically asks you to use the calculation or graphical method, you must solve the problem as asked. However, if the choice is left up to you then any correct method will lead to the correct answer.
The graphical method sometimes feels easier than calculating, but once you are confident with trigonometry and Pythagoras you will find calculating quicker and more accurate.

You've read 1 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?


