Reflections (Cambridge (CIE) O Level Maths) : Revision Note
Did this video help you?
Reflections
What is a reflection?
A reflection flips a shape across a mirror line
This is called the line of reflection
The reflected image is the same size as the original object
It has been flipped across the mirror line to a new position and orientation
The following two distances will be equal for each point:
The perpendicular distance between the original point and the mirror line
The perpendicular distance between the reflected point and the mirror line
Any points that are on the mirror line do not move
These are called invariant points
How do I reflect a shape?
STEP 1
Draw the line of reflectionThis will usually be a vertical line (
) or a horizontal line (
)
A diagonal line will either be
or
STEP 2
From each vertex on the original object measure the perpendicular distance to the mirror lineYou can usually do this by counting squares on the grid
If the line is diagonal then count the diagonals of the squares
STEP 3
Find the reflected point by measuring the same distance in the same direction from the point on the mirror line
STEP 4
Join together the reflected points and label the reflected image
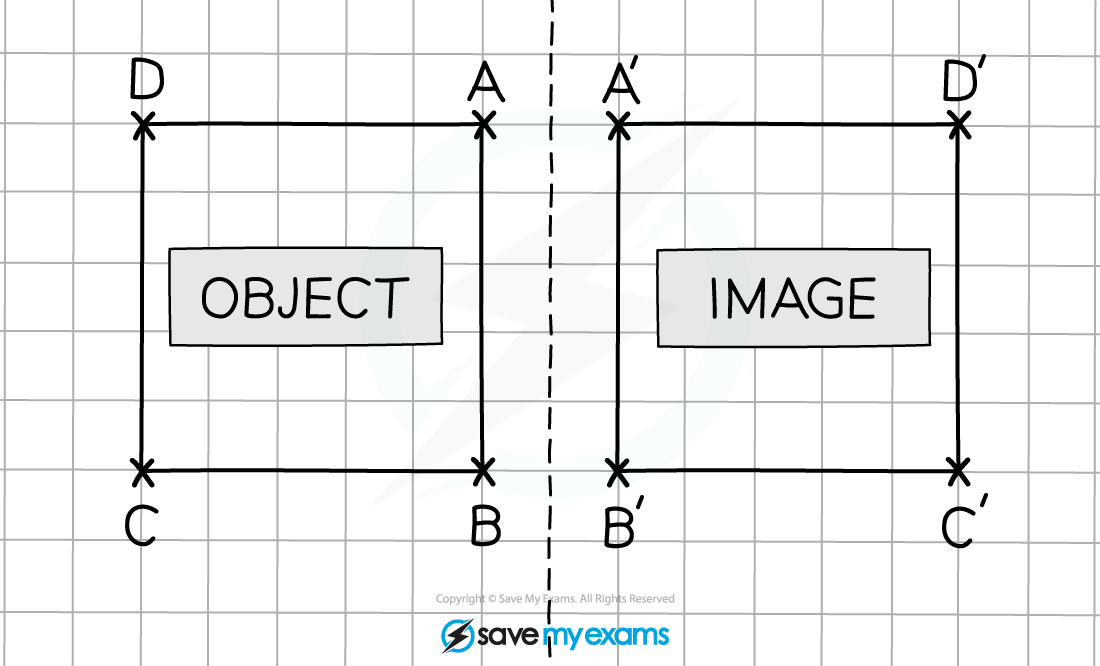
How do I reflect a shape when the line of reflection goes through the shape?
You follow the same steps as above
Part of the shape gets reflected on one side of the mirror line, and the other part gets reflected on the other side

How do I describe a reflection?
To describe a reflection, you must:
State that the transformation is a reflection
Give the mathematical equation of the mirror line
To find the equation of the reflection line:
Horizontal lines are of the form
is the number that the line passes through on the y-axis
Vertical lines are of the form
is the number that the line passes through on the x-axis
A diagonal line with a positive gradient will be
A diagonal line with a negative gradient will be
How do I reverse a reflection?
If a shape has been reflected to a new position, you can perform a single transformation to return the shape to its original position
You can reverse the reflection
The transformation to reverse a reflection, is the same transformation as the original
E.g. If a shape is reflected in the x-axis, then reflecting it again in the x-axis will return it to its original position
Examiner Tips and Tricks
It is very easy to muddle up the equations for horizontal and vertical lines, remember:
If the line crosses the x-axis then it will be
If the line crosses the y-axis then it will be
You can use tracing paper to check that your object has remained the same shape
Worked Example
(a) On the grid below, reflect shape S in the line .
State the coordinates of all of the vertices of your reflected shape.

Draw in the mirror line; will be a vertical line passing through -1 on the x-axis
Measure or count the number of units from the shape "diagonals" on the other side of the mirror line to find the position of the corresponding vertex on the reflected image

List the vertices of the reflected image.
Work your way around the shape vertex by vertex so that you don't miss any out as there are quite a few!
Vertices of the reflected shape: (1, 6), (2, 6), (2, 4), (3, 4), (3, 6), (4, 6), (4, 3), (3, 3), (3, 1), (2, 1), (2, 3), (1,3)
(b) Describe fully the single transformation that creates shape B from shape A.

You should be able to "see" where the mirror line should be without too much difficulty.
Draw the mirror line on the diagram.
You can check that it is in the correct position by measuring/counting the perpendicular distance from a pair of corresponding points on the original object and the reflected image to the same point on the mirror line.
Be careful with mirror lines near axes as it is easy to miscount.
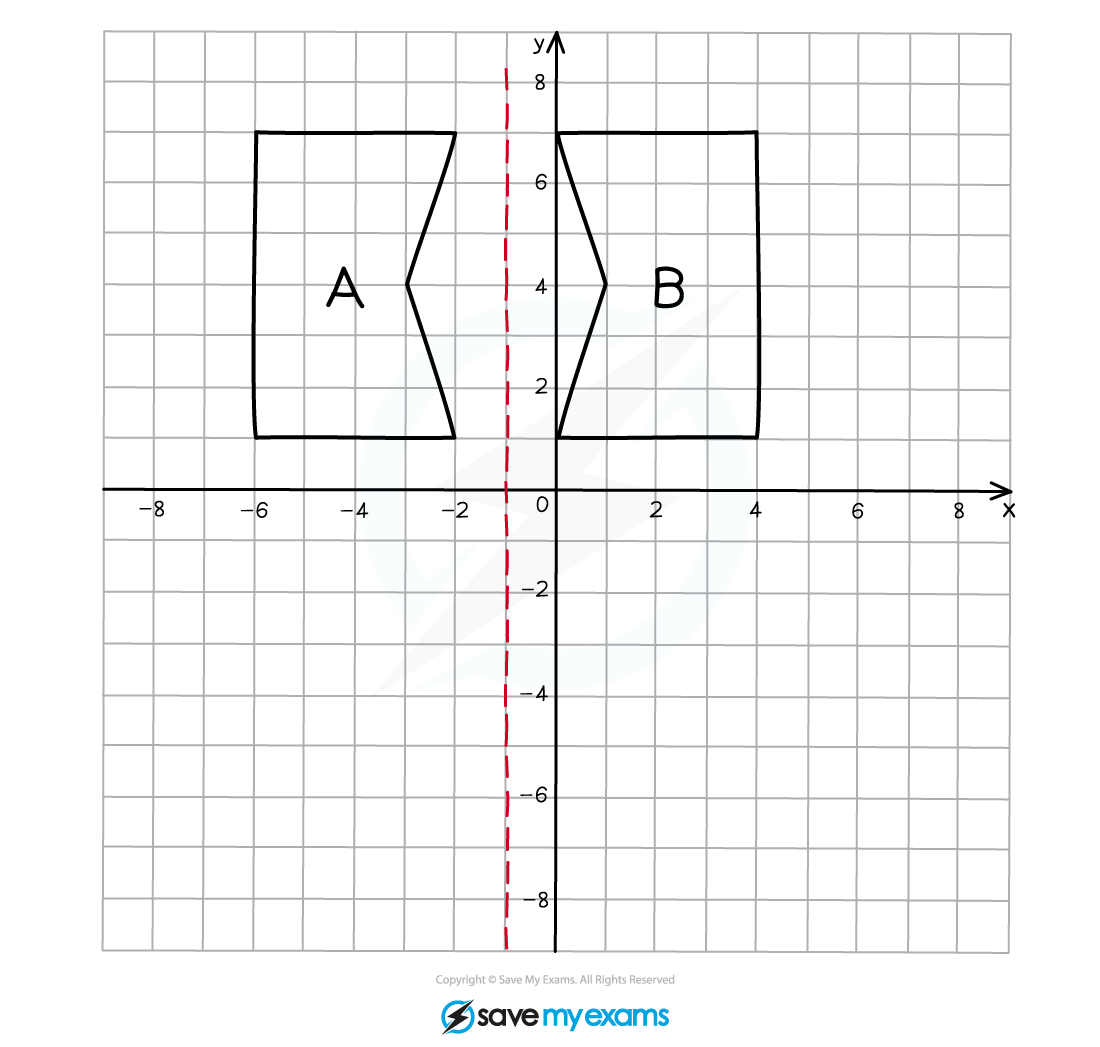
Write down that the transformation was a reflection and the equation of the mirror line.
Shape A has been reflected in the line to create shape B

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

