Angles at Centre & Circumference (Cambridge (CIE) O Level Maths) : Revision Note
Did this video help you?
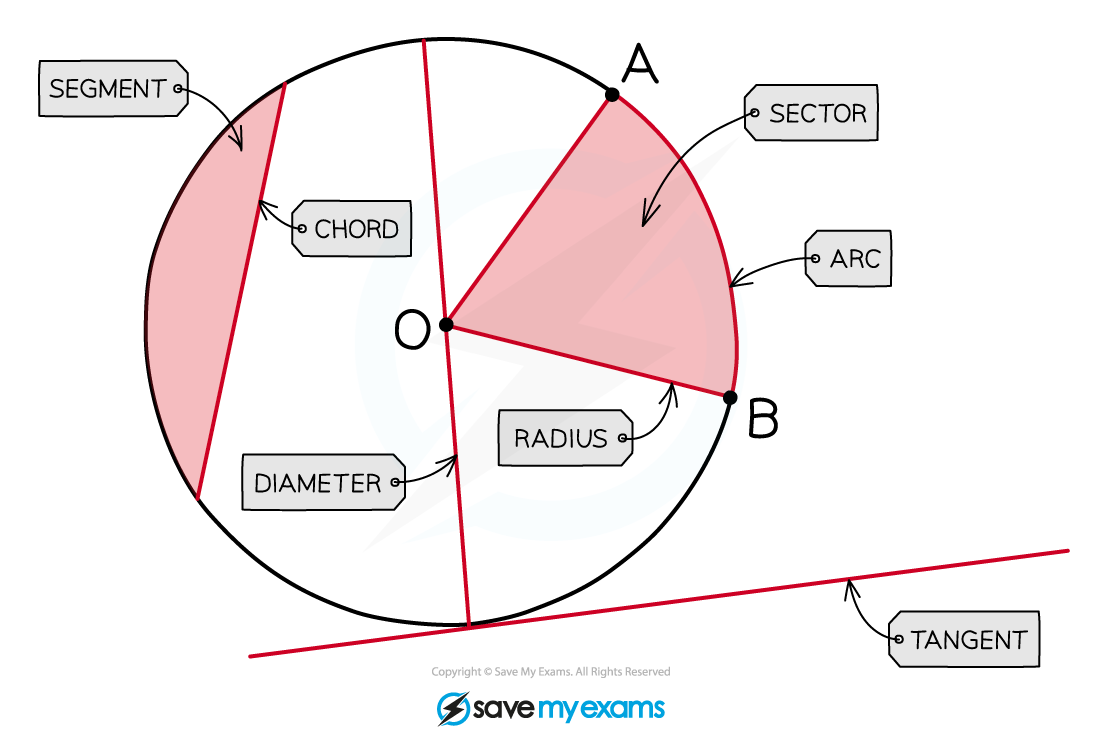
Angles at Centre & Circumference
What are circle theorems?
Circle Theorems deal with angles that occur when lines are drawn within (and connected to) a circle
You may need to use other facts and rules such as:
basic properties of lines and angles
properties of triangles and quadrilaterals
angles in parallel lines or polygons
Circle Theorem: The angle at the centre is twice the angle at the circumference
In this theorem, the chords (radii) to the centre and the chords to the circumference are both drawn from (subtended by) the ends of the same arc

To spot this circle theorem on a diagram
find any two radii in the circle and follow them to the circumference
see if there are lines from those points going to any other point on the circumference
it may look like the shape of an arrowhead
When explaining this theorem in an exam you must use the keywords:
The angle at the centre is twice the angle at the circumference
This theorem is still true when the ‘triangle parts’ overlap

It is also true when the lines form a diamond shape
You need to compare the reflex angle at the centre with the angle at the circumference
Common mistakes are to
compare the wrong angles
confuse it with a different circle theorem on cyclic quadrilaterals

Examiner Tips and Tricks
Questions often say to give “reasons” for your answer
Quote an angle fact or circle theorem for every angle you find (not just one for the final answer)
Worked Example
Find the value of in the diagram below.

Give a reason for each step of your working.
There are three radii in the diagram, AO, BO and CO
Mark these as equal length lines
Notice how they create two isosceles triangles
Base angles in isosceles triangles are equal
Angle OAB = angle OBA = 60º (isosceles triangle)

Use the circle theorem:
The angle at the centre is twice the angle at the circumference
Form an equation for
Expand the brackets and solve the equation
Base angles in isosceles triangles are equal
The angle at the centre is twice the angle at the circumference

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

