O LevelMathsCambridge (CIE)Revision NotesAlgebra & SequencesForming & Solving EquationsProblem Solving with Equations

Problem Solving with Equations (Cambridge (CIE) O Level Maths): Revision Note

Exam code: 4024

Amber

Written by: Amber

Reviewed by: Dan Finlay

Updated on

Equations & problem-solving

What is problem solving?

  • Problem solving means you are given a specific situation (real life or constructed) and you need to form and solve equations to find answers to the questions asked

  • The equations can be any type that are in the course, including

    • Linear, e.g. 2 open parentheses x plus 4 close parentheses equals 3 x

    • Quadratic, e.g. x squared minus 7 x plus 12 equals 0

  • Answers must always be given in context

    • This means related to the situation using words, phrases and units from the question

      • For example, "The population density is 225 people per square km" (not just x equals 225)

What type of algebra can come up in a problem solving question?

  • Many questions will require you to solve quadratic equations

    • You need to be able to spot these

      • This may require bringing all the terms to one side to get "= 0"

    • You are often free to choose which quadratic method to use to solve them

    • If you get two solutions, you may need to justify which solution is correct

  • You may be asked to use algebra in other settings such as geometry or numbers

    • P% is P over 100 as a decimal

    • If the ratio x space colon space open parentheses x plus 2 close parentheses is equivalent to 5 : 8, then fraction numerator x over denominator x plus 2 end fraction equals 5 over 8

  • You may have unfamiliar equations to solve

    • such as multiplying both sides by x in 12 over x equals 7 minus x to form a quadratic

Examiner Tips and Tricks

  • If part (a) asks you to prove an equation and part (b) uses that equation, you can still do part (b) without having done part (a)!

    • This means you won't lose all the marks if you can't do part (a)

Worked Example

The net of a cube is shown below.

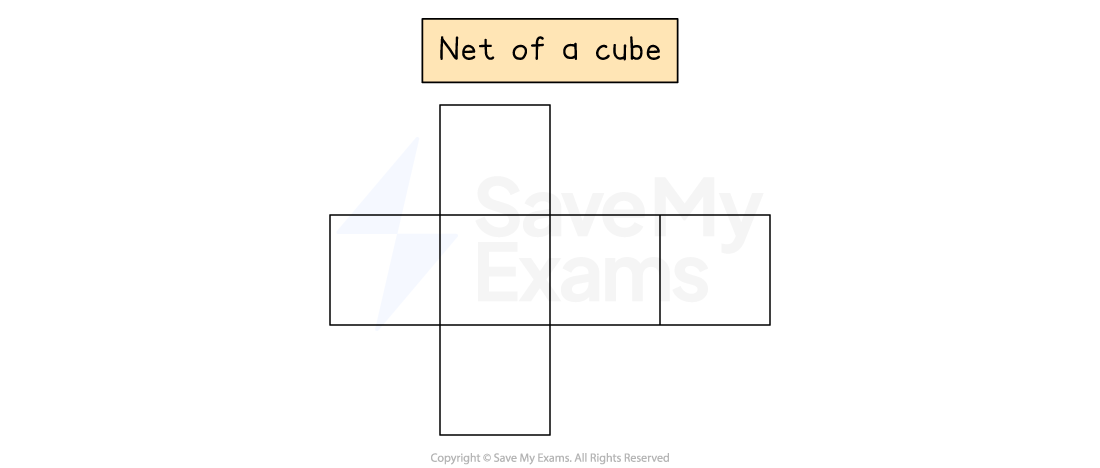
Cross shaped net of a cube

Let x cm be the side length of the cube.

Find an expression in terms of x for

(a) the perimeter of the net shown.

Count the number of edges around the outside of the net

14 edges

Multiply this number by the side length, x

The perimeter of the net shown is 14 x cm

(b) the area of the net shown.

Count the number of faces (squares) in the net

6 faces

Multiply this number by the area of one face, x cross times x equals x squared

The area of the net shown is 6 x squared cm2

When the net is folded into a cube, the difference between the volume of the cube and the surface area of the net is eight times the perimeter of the net.

(c) Show that x squared minus 6 x minus 112 equals 0.

First find an expression for the volume of the cube

This will have dimensions x cross times x cross times x

The volume is x cubed

Then find an expression for the difference between the volume and the surface area in part (b)

Subtract the surface area from the volume

x cubed minus 6 x squared

Set this difference equal to 8 times the perimeter of the net

Use the answer in part (a)

x cubed minus 6 x squared equals 8 cross times 14 x

Simplify 8 cross times 14 and bring all the terms to one side

table row cell x cubed minus 6 x squared end cell equals cell 112 x end cell row cell x cubed minus 6 x squared minus 112 x end cell equals 0 end table

You are nearly at the correct equation given in the question

Cancel both sides by x (as x cannot be zero)

To show this, you can factorise out an x first

up diagonal strike x open parentheses x squared minus 6 x minus 112 close parentheses equals 0

x squared minus 6 x minus 112 equals 0

(d) Hence, find the exact volume of the cube when the net is folded.

Hence means use the previous results

The volume of the cube is x cubed which involves an unknown, x

To find x, solve the equation in part (c), for example using the quadratic formula

table row x equals cell fraction numerator 6 plus-or-minus square root of open parentheses negative 6 close parentheses squared minus 4 cross times 1 cross times open parentheses negative 112 close parentheses end root over denominator 2 end fraction end cell row blank equals cell fraction numerator 6 plus-or-minus square root of 484 over denominator 2 end fraction end cell row blank equals cell fraction numerator 6 plus-or-minus 22 over denominator 2 end fraction end cell end table

Find the two possible answers

14 or -8

The side length x cannot be a negative number

x equals 14

Substitute this into x cubed to find the volume

14 cubed

The question asks for the answer to be exact, so do not round

The volume is 2744 cm3

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself
    Previous:Forming Equations from ShapesNext:Solving Simultaneous Equations
    Author
    Reviewer
    Amber

    Author: Amber

    Expertise: Maths Content Creator

    Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.