Second Order Derivatives (Cambridge (CIE) O Level Additional Maths): Revision Note

Second Order Derivatives

What is the second order derivative of a function?

• If you differentiate the derivative of a function (i.e. differentiate the function a second time) you get the second order derivative of the function

  • The second order derivative can be referred to simply as the second derivative

• We can write the second derivative as 

• Note the position of the powers of 2

  • differentiating twice (so) with respect to  twice (so)

• A first derivative is the rate of change of a function (the gradient)

  • a second order derivative is the rate of change of the rate of change of a function

    • i.e. the rate of change of the function’s gradient

  • A positive second derivative means the gradient is increasing

    • For instance in a u-shape, the gradient is changing from negative to positive

  • A negative second derivative means the gradient is decreasing

    • For instance in an n-shape, the gradient is changing from positive to negative

• Second order derivatives can be used to test whether a point is a minimum or maximum

• To find a second derivative, you simply differentiate twice!

  • It is important to write down your working with the correct notation, so you know what each expression means

  • For example

    • 

    • 

    • 

Stationary Points & Turning Points

What are stationary points?

• A stationary point is any point on a curve where the gradient is zero

• To find stationary points of a curve

Step 1 Find the first derivative

Step 2 Solve  to find the -coordinates of any stationary points

Step 3 Substitute those -coordinates into the equation of the curve to find the corresponding -coordinates

• A stationary point may be either a local minimum, a local maximum, or a point of inflection

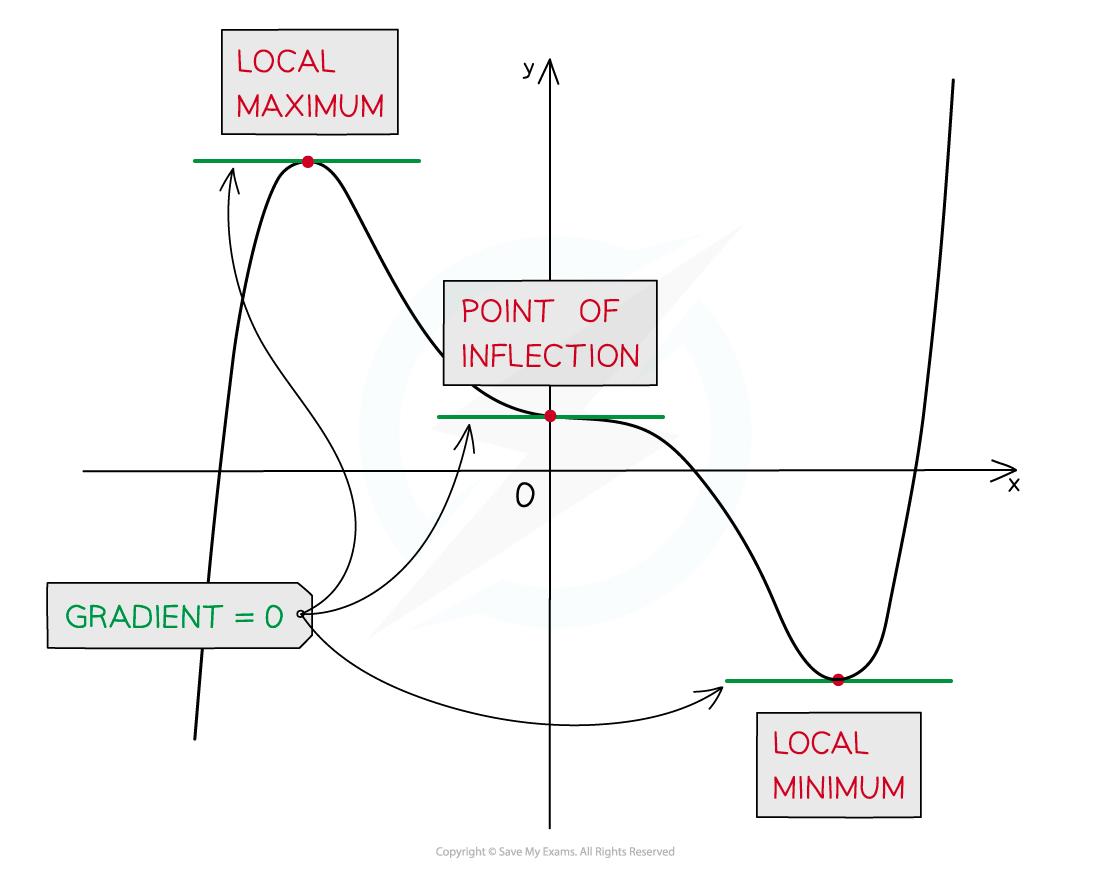
Stationary points on quadratics

• The graph of a quadratic function only has a single stationary point

• For a positive quadratic this is the minimum; for a negative quadratic it is the maximum

  • No need to talk about 'local' here, as it is the overall minimum/maximum for the whole curve

• The y value/coordinate of the stationary point is therefore the minimum or maximum value of the quadratic function

• For quadratics especially, minimum and maximum points are often referred to as turning points

Testing for Local Minimum & Maximum Points

How do I determine the nature of stationary points on a curve?

• For a graph there are two ways to determine the nature of its stationary points 

• Method A

  • Compare the signs of the first derivative, , (positive or negative) a little bit to either side of the stationary point

    • e.g. if the stationary point is at x=2 then you could find the gradient at x=1.9 and x=2.1

• Compare the signs (positive or negative) of the derivatives on the left and right of the stationary point

  • If the derivatives are negative on the left and positive on the right, the point is a local minimum (a u-shape)

  • If the derivatives are positive on the left and negative on the right, the point is a local maximum (an n-shape)

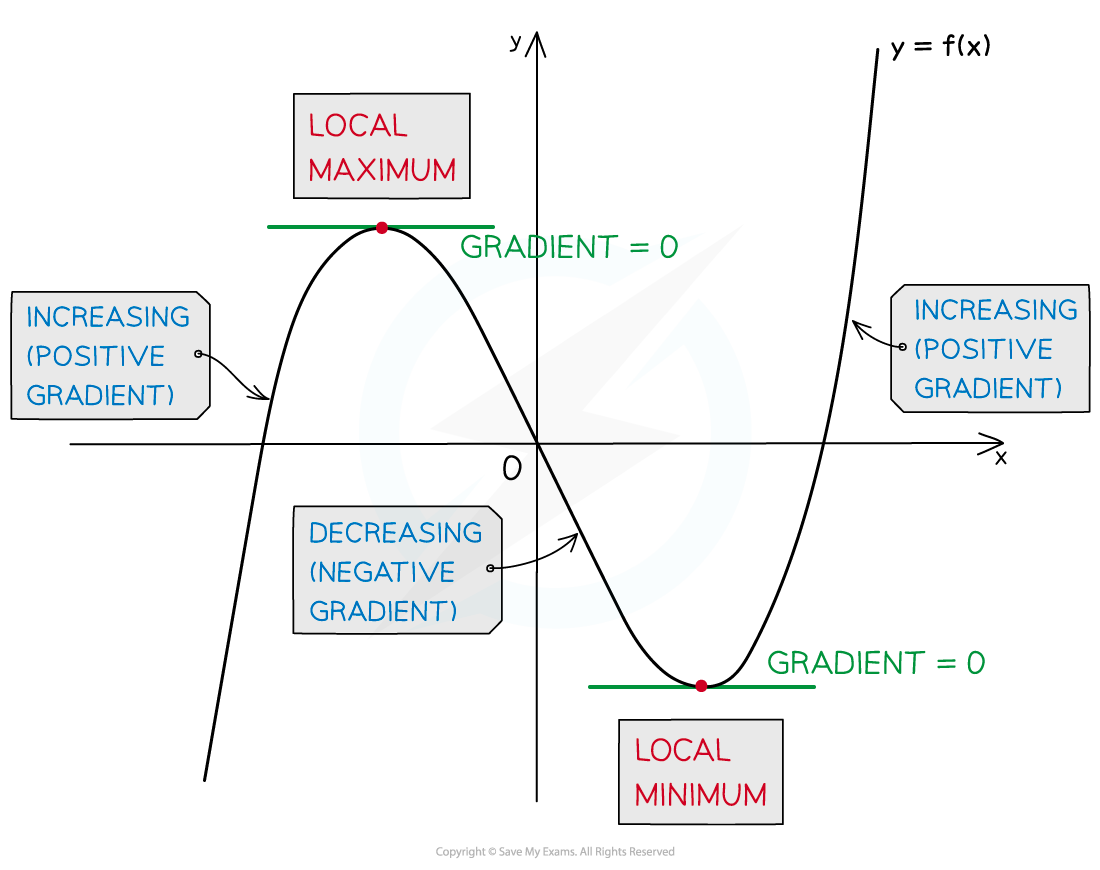
• Method B

  • Look at the sign of the second derivative (positive or negative) at the stationary point

  • Find the second derivative

  • For each stationary point find the value of at the stationary point

    • i.e. substitute the x-coordinate of the stationary point into  and evaluate

• If is positive then the point is a local minimum

  • If is negative then the point is a local maximum

  • If is zero then the point could be a local minimum, a local maximum OR a point of inflection

    • In this case you will need to use method A instead