Applications of Differentiation (Cambridge (CIE) O Level Additional Maths): Revision Note

Author

Amber

Last updated

25 December 2024

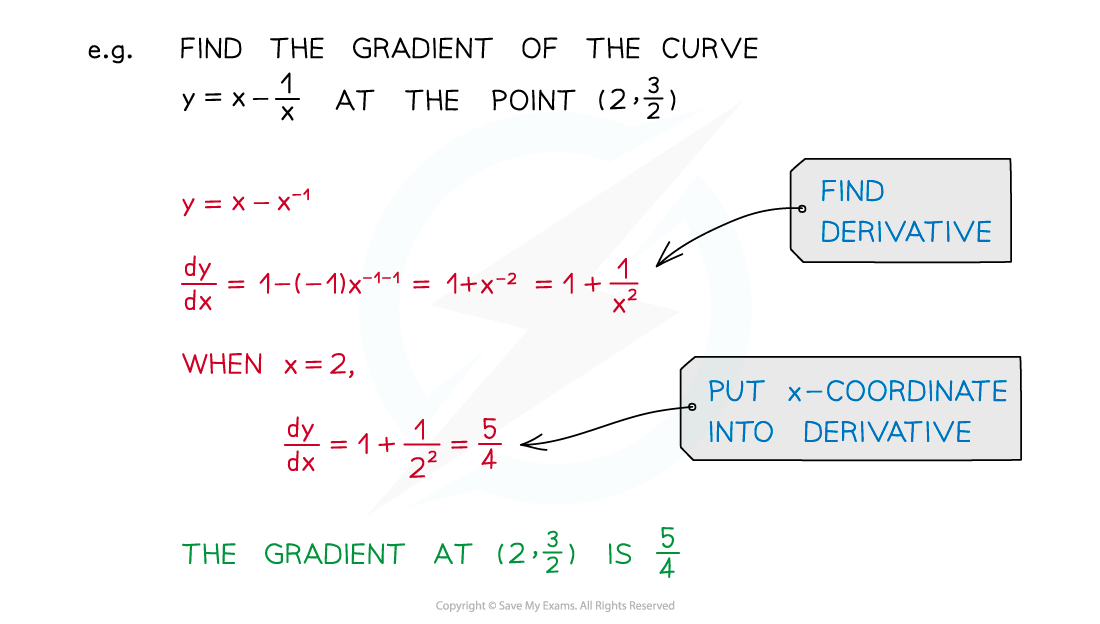
Finding Gradients

How do I use the derivative to find the gradient of a curve?

The gradient of a curve at a point is the gradient of the tangent to the curve at that point
To find the gradient of a curve, at any point on the curve
- differentiate to find $\frac{d y}{d x}$ (unless $\frac{d y}{d x}$ is already known)
- substitute the x‑coordinate of the point into the derivative $\frac{d y}{d x}$ and evaluate

Grad Tang Norm Illustr 1, A Level & AS Maths: Pure revision notes

How do I find the approximate change in y as x increases?

$gradient = \frac{change in y}{change in x}$ so, for small changes you can write
- $change in y = gradient \times change in x$
For example, if the gradient of $y = x - \frac{1}{x}$ at $x = 2$ is $\frac{5}{4}$
- what is the approximate change in $y$ as $x$ increases from $2$ to $2 + h$ , where $h$ is small?
  - $change in y = gradient \times change in x = \frac{5}{4} h$

Examiner Tips and Tricks

Read the question carefully; sometimes you are given $\frac{d y}{d x}$ and so don't need to differentiate initially - don't just automatically differentiate the first thing you see!
The following mean the same thing:
- "Find the gradient of the curve at $x = 2$ "
- "Find the gradient of the tangent at $x = 2$ "
  - the tangent gradient = curve gradient at that point
- "Find the rate of change of y with respect to x at $x = 2$ "

Worked Example

A curve has the equation $y = \frac{4}{3} x^{3} + 3 x - 8$ .

(a) Find the gradient of the curve when $x = 2$ .

$y$ is already in a form that can be differentiated

$\frac{d y}{d x} = 4 x^{2} + 3$

Substitute $x = 2$ into $\frac{d y}{d x}$

$\frac{d y}{d x} = 4 \times 2^{2} + 3 = 19$

The gradient of the curve at $x = 2$ is 19

(b) Work out the possible values of $x$ for which the rate of change of $y$ with respect to $x$ is 4.

"Rate of change" is another way of describing the derivative

$\begin{array}{rcl} \frac{d y}{d x} & = & 4 \\ 4 x^{2} + 3 & = & 4 \end{array}$

Solve this equation to find $x$
Note that it is quadratic equation so it could have up to two solutions
The question refers to 'values' implying there is (or could be) more than one value for $x$

$\begin{array}{rcl} 4 x^{2} & = & 1 \\ x^{2} & = & \frac{1}{4} \\ x & = & \pm \sqrt{\frac{1}{4}} \\ x & = & \pm \frac{1}{2} \end{array}$

The possible values of $x$ , that give a rate of change of 4, are $x = \frac{1}{2}$ and $x = - \frac{1}{2}$

Did this video help you?

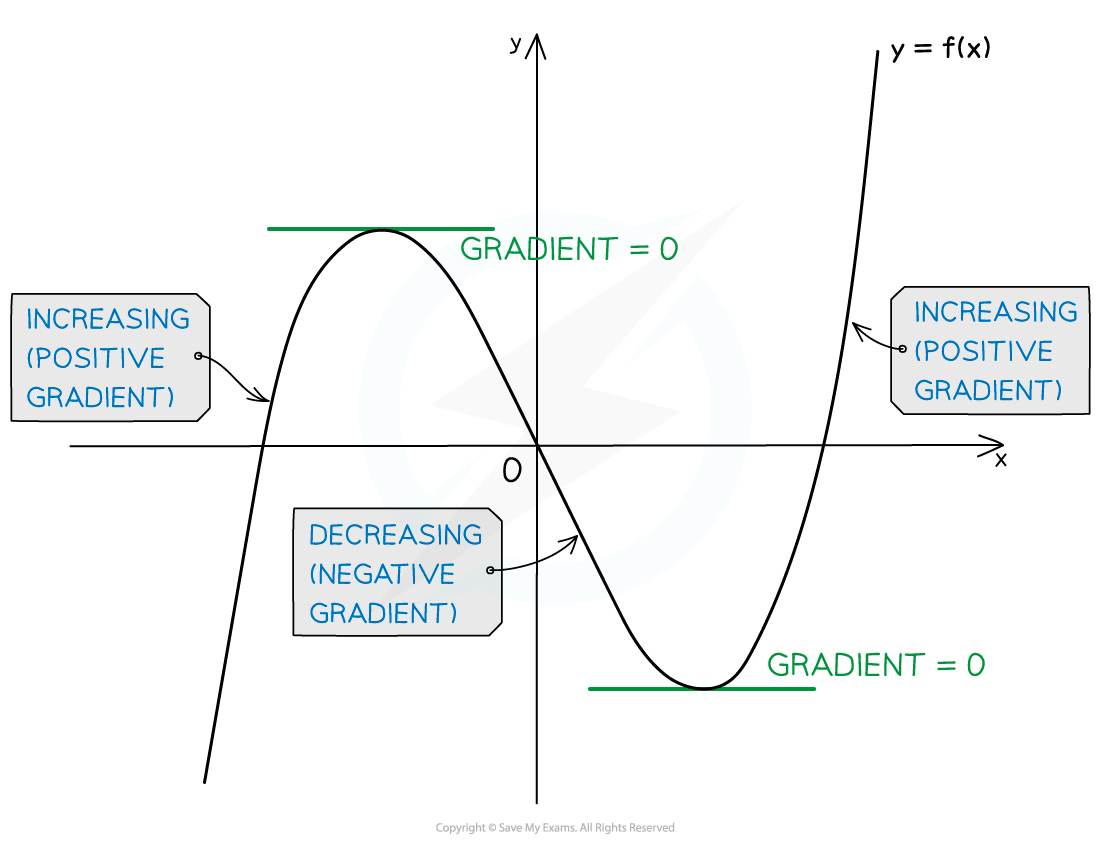
Increasing & Decreasing Functions

What are increasing and decreasing functions?

A function is increasing when $\frac{d y}{d x} > 0$ (the gradient is positive)
- This means graph of a function goes up as $x$ increases
A function is decreasing when $\frac{d y}{d x} < 0$ (the gradient is negative)
- This means graph of a function goes down as $x$ increases

Incr Decr Illustr 1, A Level & AS Maths: Pure revision notes

How do I find where functions are increasing or decreasing?

To identify the intervals on which a function is increasing or decreasing

STEP 1

Find the derivative f'(x)

STEP 2

Solve the inequalities

$f' (x) > 0$ (for increasing intervals) and/or

$f' (x) < 0$ (for decreasing intervals)

Most functions are a combination of increasing, decreasing and stationary
- a range of values of $x$ (interval) is given where a function satisfies each condition
- e.g. The function $f (x) = x^{2}$ has derivative $f^{'} (x) = 2 x$ so
  - $f (x)$ is decreasing for $x < 0$
  - $f (x)$ is stationary at $x = 0$
  - $f (x)$ is increasing for $x > 0$

To identify the intervals (the range of $x$ values) for which a curve is increasing or decreasing you need to:

Find the derivative $\frac{d y}{d x}$
Solve the inequalities $\frac{d y}{d x} > 0$ (for increasing intervals) or $\frac{d y}{d x} < 0$ (for decreasing intervals)

Examiner Tips and Tricks

In an exam, if you need to show a function is increasing or decreasing you can use either strict (<, >) or non-strict (≤, ≥) inequalities
- You will get the marks either way in this course

Worked Example

For what values of $x$ is $y = 2 x^{3} - 3 x^{2} + 5$ a decreasing function?

The function is decreasing when its gradient $(\frac{d y}{d x})$ is less than 0.

Find the derivative of the function by differentiating.

$\begin{array}{rcl} \frac{d y}{d x} & = & 6 x^{2} - 6 x \end{array}$

Solve the inequality $\frac{d y}{d x} < 0$ to find the set of values where the gradient is negative.

$\begin{array}{rcl} 6 x^{2} - 6 x & < & 0 \end{array}$

Factorise.

$\begin{array}{rcl} 6 x (x - 1) & < & 0 \end{array}$

The solutions to $\frac{d y}{d x} = 0$ are $x = 0$ and $x = 1$ . Find the correct way around for the inequalities by considering the graph of $\frac{d y}{d x}$ . The graph is a positive quadratic, so the function is negative between the values of 0 and 1 (where it is below the $x$ -axis).

Considering a sketch of the graph of the gradient function may help you see this.

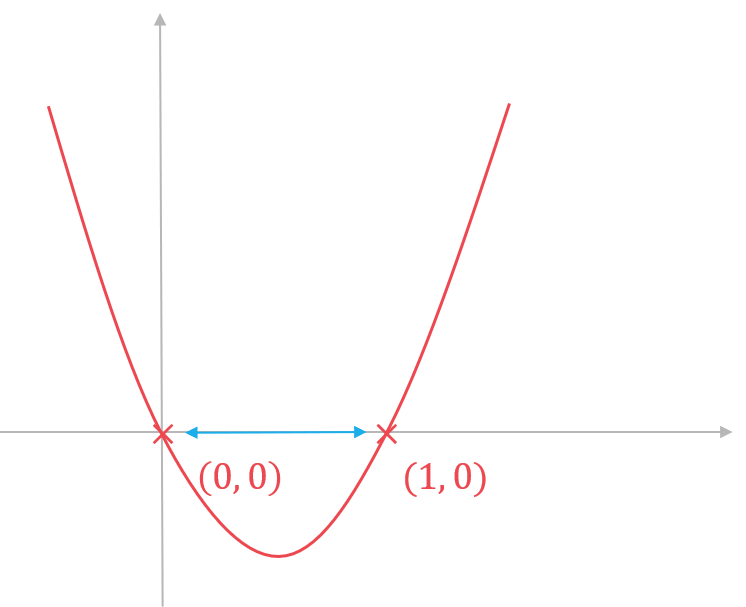
3CqZzydq_aqa-fm-increasing-and-decreasing-functions-rn-diagram-we-1

You can check your answers by considering a sketch of the original function, it should be decreasing at the point where $0 < x < 1 .$

aqa-fm-increasing-and-decreasing-functions-rn-diagram-we-2

$0 < x < 1$

Did this video help you?

Tangents & Normals

What is a tangent?

At any point on the graph of a (non-linear) function, the tangent is the straight line that touches the graph at a point without crossing through it
Its gradient is given by the derivative function

How do I find the equation of a tangent?

To find the equation of a straight line, a point and the gradient are needed
The gradient, $m$ , of the tangent to the function $y = f (x)$ at ${(x}_{1}, y_{1})$ is $f' (x_{1})$
- You can find this by differentiating the function, and then substituting the $x$ -coordinate of the point into the derivative
Therefore find the equation of the tangent to the function $y = f (x)$ at the point ${(x}_{1}, y_{1})$ by substituting the gradient, $f' (x_{1})$ , and point ${(x}_{1}, y_{1})$ into $y - y_{1} = m (x - x_{1})$ , giving:
- $y - y_{1} = f^{'} (x_{1}) (x - x_{1})$
(You could also substitute into $y = m x + c$ )

What is a normal?

At any point on the graph of a (non-linear) function, the normal is the straight line that passes through that point and is perpendicular to the tangent

How do I find the equation of a normal?

The gradients of two perpendicular lines are negative reciprocals
- This means that if $m_{1}$ is the gradient of the first line and $m_{2}$ is the gradient of a line perpendicular to the first line, then $m_{2} = \frac{- 1}{m_{1}}$
- Rearranging the formula above, $m_{1} \times m_{2} = - 1$ is a useful way to test whether two lines are perpendicular
Therefore gradient of the normal to the function $y = f (x)$ at ${(x}_{1}, y_{1})$ is $\frac{- 1}{f' (x_{1})}$
Find the equation of the normal to the function $y = f (x)$ at the point ${(x}_{1}, y_{1})$ by using $y - y_{1} = \frac{- 1}{f^{'} (x_{1})} (x - x_{1})$
- (or $y = \frac{- 1}{f^{'} (x_{1})} x + c$ )

Examiner Tips and Tricks

To be successful in this topic, first make sure you are confident with finding the equation of a straight line!

Worked Example

The function $f (x)$ is defined by

$f (x) = 2 x^{4} + \frac{3}{x^{2}} x \neq 0$

a) Find an equation for the tangent to the curve $y = f (x)$ at the point where $x = 1$ , giving your answer in the form $y = m x + c$ .

First find the derivative $f' (x)$ by differentiating

Start by rewriting $f (x)$ as powers of x

$f (x) = 2 x^{4} + 3 x^{- 2}$

Now differentiate

$f' (x) = 8 x^{3} - 6 x^{- 3}$

Now substitute $x = 1$ into $f' (x)$ to find the gradient of the tangent

$\begin{array}{rcl} f' (1) & = & 8 {(1)}^{3} - 6 {(1)}^{- 3} \\ = & 8 - 6 \\ = & 2 \end{array}$

We also need the y-coordinate, so substitute $x = 1$ into $f (x)$ also

$\begin{array}{rcl} f (1) & = & 2 {(1)}^{4} + 3 {(1)}^{- 2} \\ = & 2 + 3 \\ = & 5 \end{array}$

Now we can substitute the point (1, 5) and the gradient, 2, into $y - y_{1} = m (x_{1}) (x - x_{1})$

$\begin{array}{rcl} y - 5 & = & 2 (x - 1) \end{array}$

Note that we are asked for the final answer in the form $y = m x + c$ , so rearrange to this form

$\begin{array}{rcl} y - 5 & = & 2 x - 2 \end{array}$

$y = 2 x + 3$

b) Find an equation for the normal at the point where $x = 1$ , giving your answer in the form $a x + b y + d = 0$ , where $a$ , $b$ and $d$ are integers.

We already have the gradient of the tangent; the gradient of the normal is $\frac{- 1}{m}$ where $m$ is the gradient of the tangent

gradient of normal = $\frac{- 1}{2}$

Substitute the point (1, 5) from part (a) and the gradient of the normal into $y - y_{1} = m (x - x_{1})$

$\begin{array}{rcl} y - 5 & = & (\frac{- 1}{2}) (x - 1) \end{array}$

And rearrange into the form required

$\begin{array}{rcl} y - 5 & = & - \frac{1}{2} x + \frac{1}{2} \\ \frac{1}{2} x + y - 5 \frac{1}{2} & = & 0 \end{array}$

Note that $a$ , $b$ and $d$ must be integers so multiply by 2 to clear the fractions

$\begin{array}{rcl} x + 2 y - 11 & = & 0 \end{array}$

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Quotient RuleNext:Second Order Derivatives

Applications of Differentiation (Cambridge (CIE) O Level Additional Maths): Revision Note

Finding Gradients

How do I use the derivative to find the gradient of a curve?

How do I find the approximate change in y as x increases?

Increasing & Decreasing Functions

What are increasing and decreasing functions?

How do I find where functions are increasing or decreasing?

Tangents & Normals

What is a tangent?

How do I find the equation of a tangent?

What is a normal?

How do I find the equation of a normal?

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Algebra & Functions

Functions

Language of Functions

Inverse Functions

Composite Functions

Quadratic Functions

Solving Quadratics by Factorising

Quadratic Formula

Completing the Square

Quadratic Equation Methods

Discriminants

Quadratic Graphs

Quadratic Inequalities

Factors of Polynomials

Operations with Polynomials

Polynomial Division

Factor & Remainder Theorem

Solving Cubic Equations

Equations, Inequalities & Graphs

Modulus Functions

Graphs of Cubic Polynomials

Simultaneous Equations

Linear Simultaneous Equations

Quadratic Simultaneous Equations

Logarithmic & Exponential Functions

Exponential Functions

Logarithmic Functions

Laws of Logarithms

Exponential Equations

Transforming Relationships to Linear Form

Coordinate Geometry

Straight-Line Graphs

Linear Graphs

Parallel & Perpendicular Lines

Coordinate Geometry of the Circle

Equation of a Circle

Tangents to Circles

Intersection of Two Circles

Trigonometry

Circular Measure

Radian Measure

Arcs & Sectors

Trigonometry

Trigonometric Functions

The Unit Circle

Graphs of Trigonometric Functions

Trigonometric Identities

Solving Trigonometric Equations

Trigonometric Proof

Sequences & Series

Permutations & Combinations

Permutations

Combinations

Problem Solving with Permutations & Combinations

Binomial Theorem

Binomial Theorem

Arithmetic & Geometric Progressions

Language of Sequences & Series

Arithmetic Progressions

Geometric Progressions

Vectors

Vectors in Two Dimensions

Introduction to Vectors

Vector Addition

Problem Solving using Vectors