Revision NotesExam QuestionsPast Papers
O LevelFurther MathsCambridge (CIE)Additional MathsRevision NotesAlgebra & FunctionsQuadratic FunctionsDiscriminants

Discriminants (Cambridge (CIE) O Level Additional Maths): Revision Note

Paul

Author

Paul

Last updated

Discriminants

What is a discriminant?

  • The discriminant is the part of the quadratic formula that is under the square root sign 

  • It is b squared minus 4 a c

    • The quadratic formula, in full, is

x equals fraction numerator negative b plus-or-minus square root of b squared minus 4 a c end root over denominator 2 a end fraction

where the quadratic equation is written in the form

a x squared plus b x plus c equals 0

  • It is sometimes denoted by the Greek letter straight capital delta (capital delta)

Worked Example

Find, in terms of the constant k, the discriminant of the quadratic equation 3 x squared plus 2 k x minus k equals k x squared minus 4 k x plus 2.

First write the quadratic equation in the form a x squared plus b x plus c equals 0.

table row cell 3 x squared minus k x squared plus 2 k x plus 4 k x minus k minus 2 end cell equals 0 row cell open parentheses 3 minus k close parentheses x squared plus 6 k x minus open parentheses k plus 2 close parentheses end cell equals 0 end table

It can be easier/clearer to pick out a comma space b and c first, before finding the discriminant.

table attributes columnalign right center left columnspacing 0px end attributes row a equals cell 3 minus k end cell row b equals cell 6 k end cell row c equals cell negative open parentheses k plus 2 close parentheses end cell end table

The discriminant is b squared minus 4 a c.

table row increment equals cell open parentheses 6 k close parentheses squared minus 4 cross times open parentheses 3 minus k close parentheses cross times negative open parentheses k plus 2 close parentheses end cell row increment equals cell 36 k squared plus 4 open parentheses 6 plus k minus k squared close parentheses space end cell end table

bold increment bold equals bold 32 bold italic k to the power of bold 2 bold plus bold 4 bold italic k bold plus bold 24

Applications of Discriminant

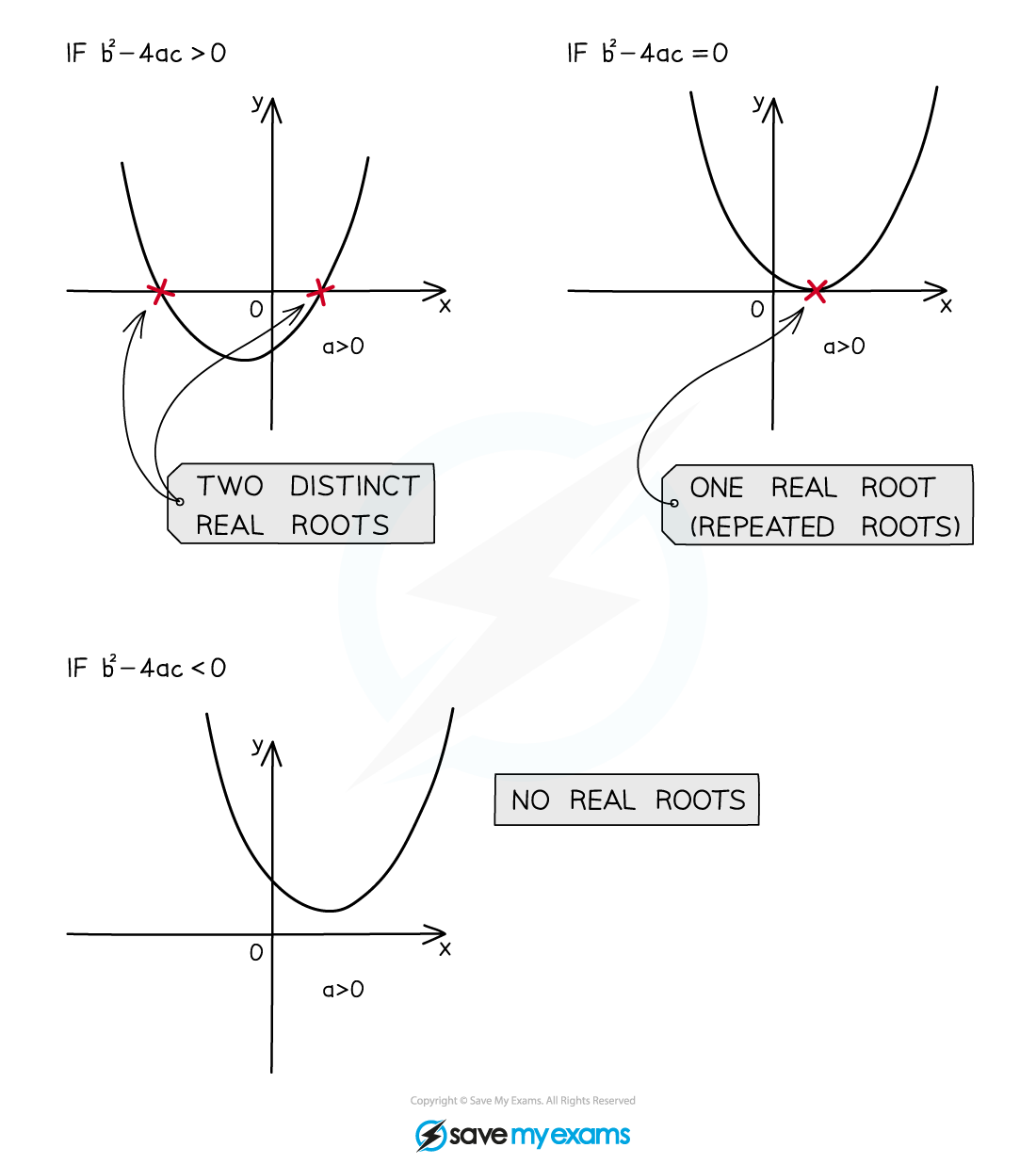
How does the value of the discriminant affect roots?

  • There are three options for the outcome of the discriminant:

    • If b squared minus 4 a c space greater than 0 the square root part of the quadratic formula can be calculated leading to two solutions (values of x)

      • i.e. two different real roots

    • If  b squared minus 4 a c equals 0 the square root part of the quadratic formula will be zero leading to one solution

      • i.e. one repeated root or two equal roots

    • If  b squared minus 4 a c space less than 0 the square root part of the quadratic formula cannot be calculated leading to no solutions

      • i.e. no (real) roots

How do I sketch quadratic graphs using the discriminant?

  • If b squared minus 4 a c space greater than 0 the quadratic equation has two different real roots

    • The graph of the quadratic will intersect the x-axis twice (at the roots)

  • If  b squared minus 4 a c equals 0 the quadratic equation has two equal roots (one root)

    • The graph of the quadratic will intersect (touch) the x-axis once (at the root)

  • If  b squared minus 4 a c space less than 0 the quadratic equation has no (real) roots

    • The graph of the quadratic will not intercept the x-axis

The discriminant determines how many roots a quadratic graph has

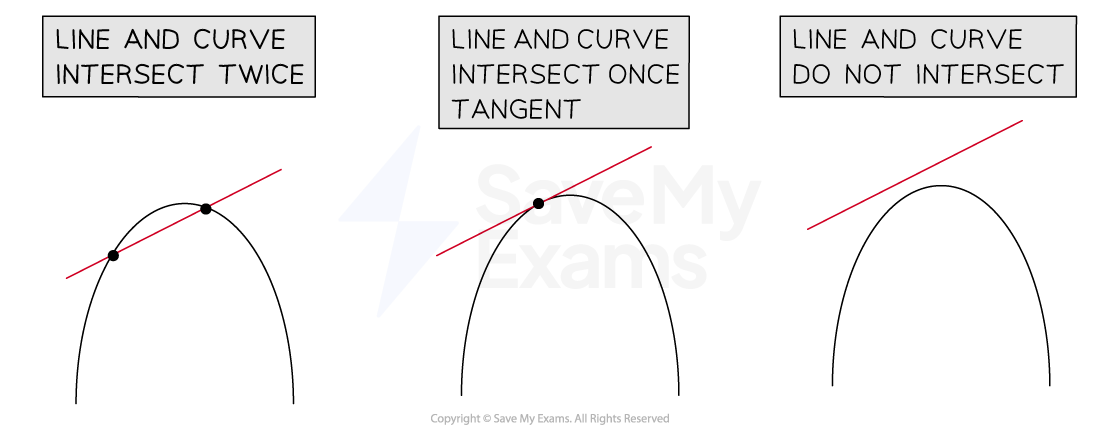
How do I use the discriminant to find the number of intersections between a line and a curve?

  • For the graphs of two functions, y equals straight f open parentheses x close parentheses and y equals straight g open parentheses x close parentheses where

    • straight f open parentheses x close parentheses is quadratic

    • straight g open parentheses x close parentheses is linear

the number of intersections between the graphs can be found using the discriminant.

  • STEP 1

    • Set straight f open parentheses x close parentheses equals straight g open parentheses x close parentheses

  • STEP 2

    • Rearrange into the form straight h open parentheses x close parentheses equals 0 such that straight h open parentheses x close parentheses is in the quadratic form a x squared plus b x plus c equals 0

  • STEP 3

    • Find the discriminant and thus determine the number of intersections between the graphs of y equals straight f open parentheses x close parenthesesand y equals straight g open parentheses x close parentheses

      • if b squared minus 4 a c greater than 0 (two real roots) the graphs intersect twice

      • if b squared minus 4 a c equals 0 (equal roots) the graphs intersect once

      • this means the line (straight g open parentheses x close parentheses) is a tangent to the curve (straight f open parentheses x close parentheses)

      • if b squared minus 4 a c less than 0 (no real roots) the graphs do not intersect

The possible intersections between a line and a quadratic

Worked Example

Show that the line with equation y equals 3 x minus 7 is tangent to the curve with equation y equals open parentheses x plus 3 close parentheses open parentheses x minus 2 close parentheses.

STEP 1 - set the equations of the line and curve equal to each other.

3 x minus 7 equals open parentheses x plus 3 close parentheses open parentheses x minus 2 close parentheses

STEP 2 - rearrange to quadratic form.

table row cell 3 x minus 7 end cell equals cell x squared plus x minus 6 end cell row cell x squared minus 2 x plus 1 end cell equals 0 end table

STEP 3 - find the discriminant and interpret its value.

increment equals open parentheses negative 2 close parentheses squared minus 4 open parentheses 1 close parentheses open parentheses 1 close parentheses equals 0

Since the discriminant is zero, the line and the curve intersect at one point only. Therefore the line is a tangent to the curve.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Quadratic Equation MethodsNext:Quadratic Graphs
    Paul

    Author: Paul

    Expertise: Maths Content Creator (Previous)

    Paul has taught mathematics for 20 years and has been an examiner for Edexcel for over a decade. GCSE, A level, pure, mechanics, statistics, discrete – if it’s in a Maths exam, Paul will know about it. Paul is a passionate fan of clear and colourful notes with fascinating diagrams.