Logarithmic Functions (Cambridge (CIE) O Level Additional Maths): Revision Note

Logarithmic Functions

What are logarithmic functions?

• A logarithm is the inverse of raising to a power 

• If  then 

  • 

  • is called the base of the logarithm

• Try to get used to ‘reading’ logarithm statements to yourself

  •   would be read as “the power that you raise ... to, to get ..., is ”

  • So  would be read as “the power that you raise 5 to, to get 125, is 3”

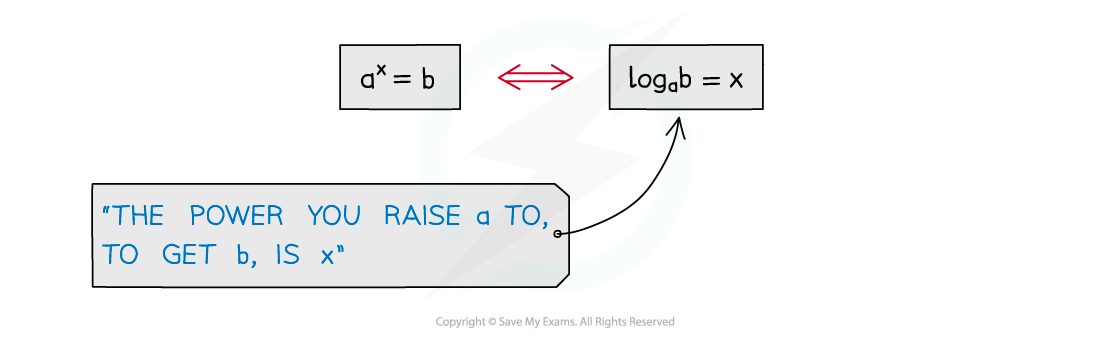
• A logarithm is the inverse of raising to a power so we can use rules to simplify logarithmic functions

Why use logarithms?

• Logarithms allow us to solve equations where the exponent is the unknown value

  • We can solve some of these by inspection

    • For example, for the equation 2^x = 8 we know that x must be 3

  • Logarithms allow use to solve more complicated problems

    • For example, the equation 2^x = 10 does not have a clear answer

    • Instead, we can use our calculator to find the value of

How do I use logarithms?

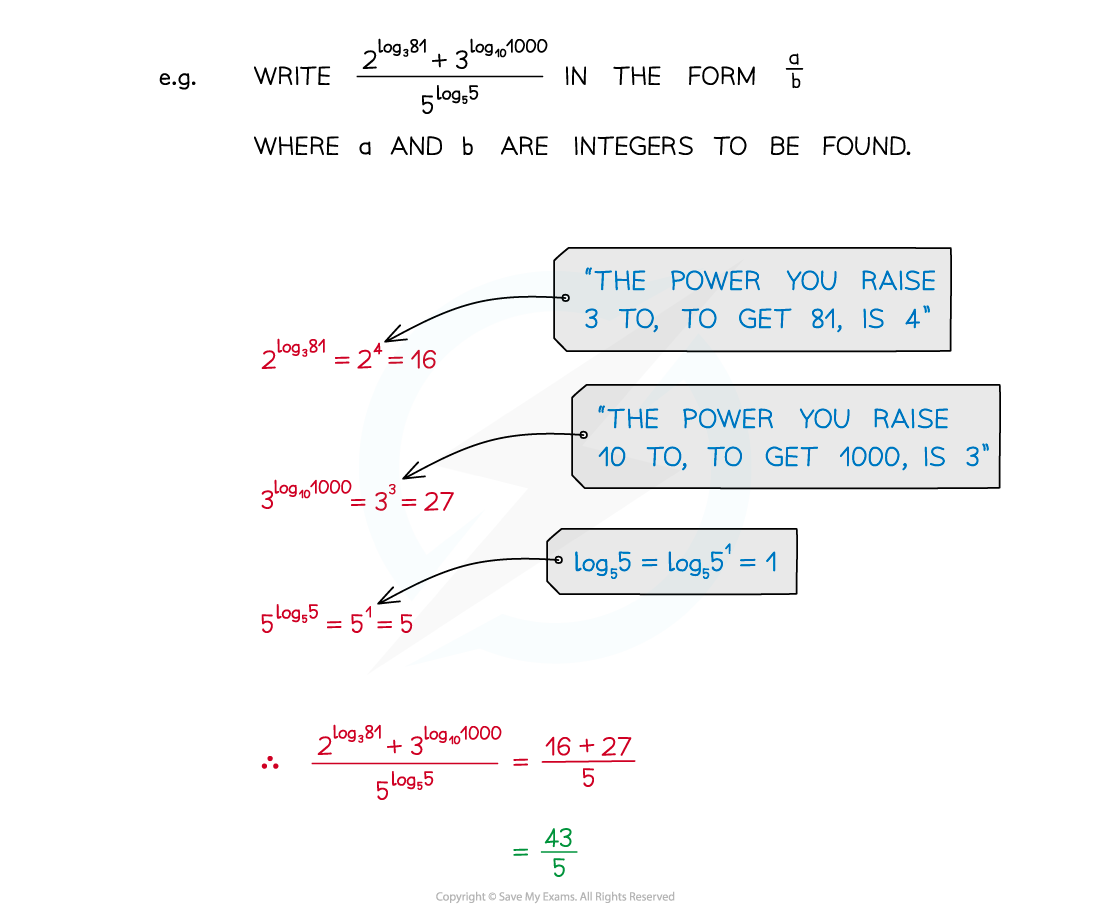
•  Recognising the rules of logarithms allows expressions to be simplified

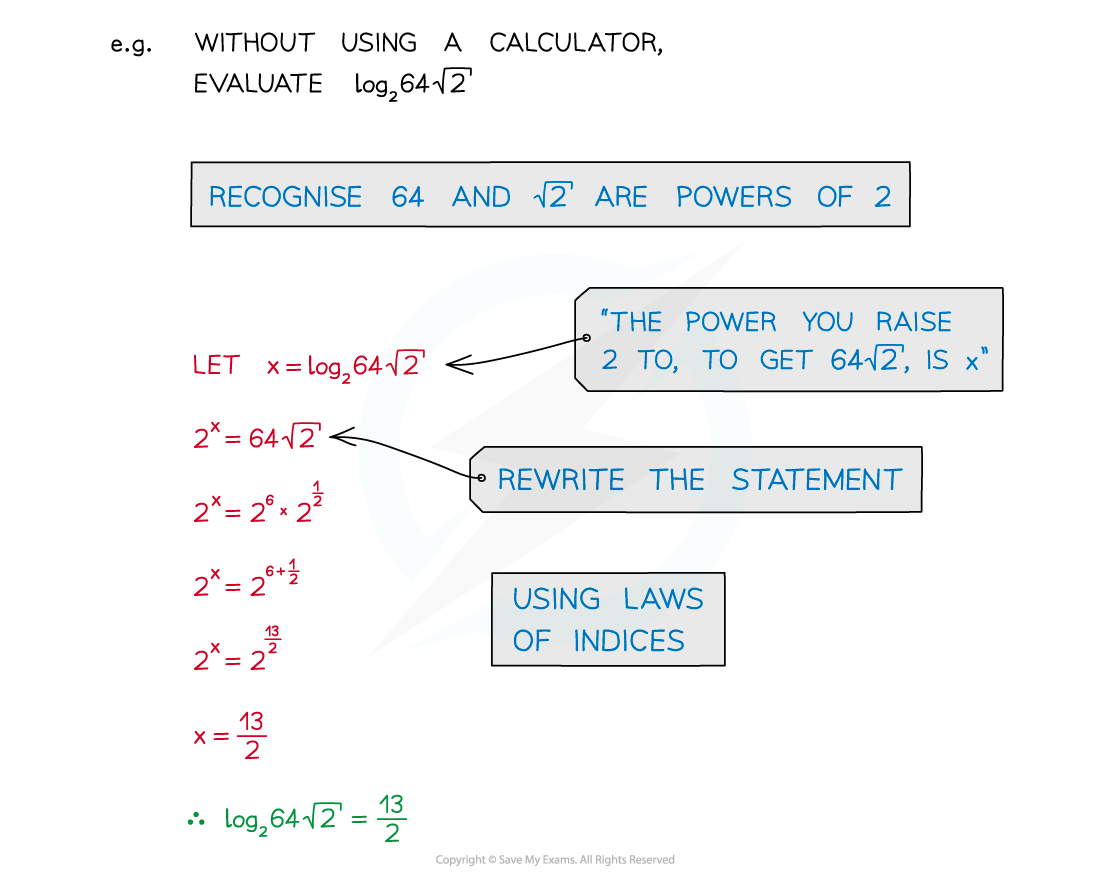
• Recognition of common powers helps in simple cases

  • Powers of 2: 2⁰ = 1, 2¹ = 2, 2² = 4, 2³ = 8, 2⁴ =16, …

  • Powers of 3: 3⁰ = 1, 3¹ = 3, 3² = 9, 3³ = 27, 3⁴ = 81, …

  • The first few powers of 4, 5 and 10 should also be familiar

  For more awkward cases a calculator is needed 

  

• Calculators can have, possibly, three different logarithm buttons

• This button allows you to type in any number for the base

• Natural logarithms (see “e”)

• Shortcut for base 10 although SHIFT button needed 

• Before calculators, logarithmic values had to be looked up in printed tables

What notation might I see with logarithms?

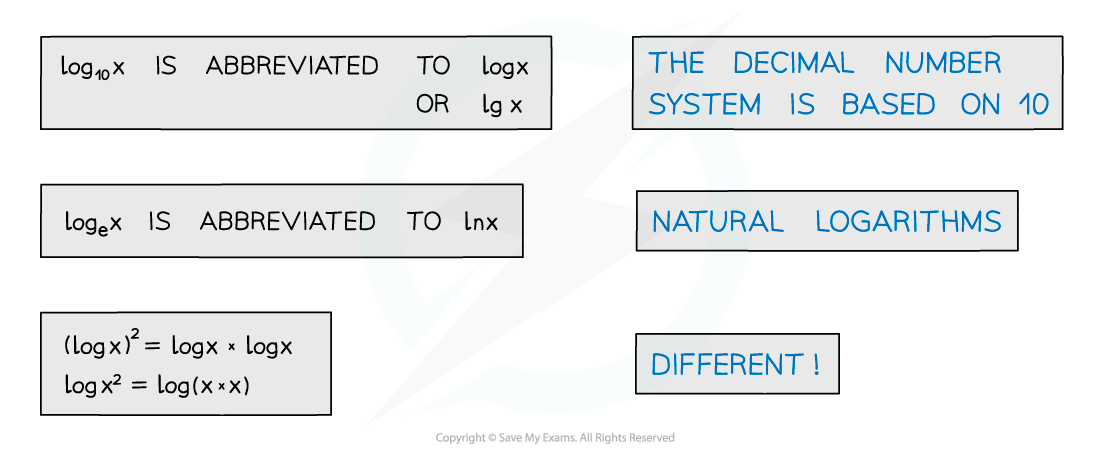
• 10 is a common base

  • log₁₀ x is abbreviated to log x or lg x

• The value e is another common base

  • log_e x is abbreviated to ln x

• (log x)² ≠ log x²

ln x

What is ln? 

• ln is a function that stands for natural logarithm

• It is a logarithm where the base is the constant "e"

  • 

  • It is important to remember that ln is a function and not a number

• The natural logarithm () and the exponential function () are inverses of each other 

• It is defined for all positive numbers ()

  • cannot be defined for negative numbers or 

What are the properties of ln? 

• Using the definition of a logarithm you can see

  • 

  • 

  •  

  • is only defined for positive x

How can I solve equations involving e & ln? 

• The functions and  are inverses of each other

  • If  then 

  • If  then 

  • If  then 

  • If  then 

• If your equation involves "e" then try to get all the "e" terms on one side

  • If "e" terms are multiplied, you can add the powers

    •  

    • You can then apply ln to both sides of the equation

  • If "e" terms are added, try transforming the equation with a substitution

    • For example: If  then

    • You can then solve the resulting equation (usually a quadratic)

    • Once you solve for y then solve for x using the substitution formula

• If your equation involves "ln", try to combine all "ln" terms together

  • Use the laws of logarithms to combine terms into a single term

  • If you have  then solve 

  • If you have  then solve