Revision NotesExam QuestionsPast Papers
O LevelFurther MathsCambridge (CIE)Additional MathsRevision NotesAlgebra & FunctionsFunctionsLanguage of Functions

Language of Functions (Cambridge (CIE) O Level Additional Maths): Revision Note

Paul

Author

Paul

Last updated

Did this video help you?

Introduction to Functions

What is a mapping?

  • A mapping takes an 'input' from one set of values to an 'output' in another

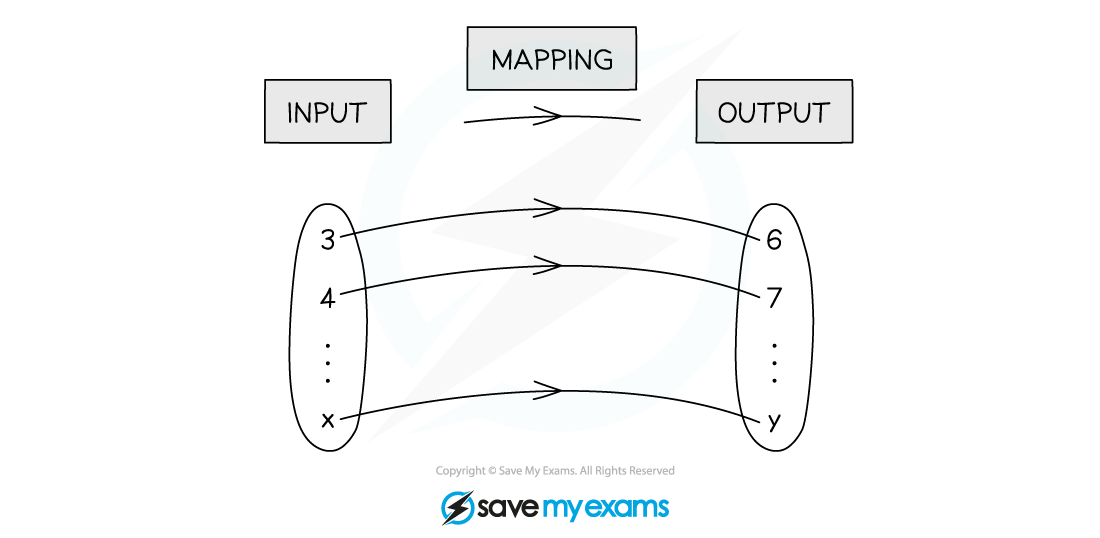
Input and output of a mapping

  • Mappings can be

    • 'many-one' (many 'input' values map to one 'output' value)

    • 'one-one' (one 'input' value maps to one 'output' value)

      • You may also come across 'many-many' and 'one-many' functions

What is a function?

  • A function is a mapping where every 'input' value maps to a single 'output'

  • Therefore only many-one and one-one mappings are functions

What notation is used for functions?

  • Functions are denoted by straight f open parentheses x close parentheses comma space straight g open parentheses x close parentheses, etc

    • e.g.  straight f open parentheses x close parentheses equals x squared minus 3 x plus 2 

    • These would be pronounced as 'f of x', 'g of x', etc

  • There is an alternative notation

    • e.g.  straight f colon x rightwards arrow from bar x squared minus 3 x plus 2

    • Which may be pronounced 'the function f maps x to x-squared minus three x plus two'

How does a function work?

  • A function has an input open parentheses x close parentheses and output left parenthesis straight f open parentheses x close parentheses space or space space y right parenthesis

  • Whatever goes in the bracket (instead of x) with f, replaces the x on the other side

    • This is the input

  • If the input is known, the output can be calculated

    • For example, given the function straight f left parenthesis x right parenthesis space equals space 2 x space plus space 1

      • straight f left parenthesis 3 right parenthesis space equals space 2 space cross times space 3 space plus space 1 equals 7

      • straight f left parenthesis negative 4 right parenthesis space equals space 2 space cross times space left parenthesis negative 4 right parenthesis space plus space 1 space equals space minus 7

      • straight f left parenthesis a right parenthesis space equals space 2 a space plus space 1

  • If the output is known, an equation can be formed and solved to find the input

    • For example, given the function straight f left parenthesis x right parenthesis space equals space 2 x space plus space 1

      • If straight f left parenthesis x right parenthesis space equals space 15, the equation 2 x space plus space 1 space equals space 15 can be formed

      • Solving this equation gives an input of 7

Worked Example

A function is defined as straight f open parentheses x close parentheses space equals space 3 x to the power of 2 space end exponent minus space 2 x space plus space 1.

a) Find straight f open parentheses 7 close parentheses.

  

The input is x space equals space 7, so substitute 7 into the expression everywhere you see an x.

  

straight f open parentheses 7 close parentheses space equals space 3 open parentheses 7 close parentheses squared space minus space 2 open parentheses 7 close parentheses space plus space 1

  

Calculate.

  

table row cell straight f open parentheses 7 close parentheses space end cell equals cell space 3 open parentheses 49 close parentheses space minus space 14 space plus space 1 end cell row blank equals cell space 147 space minus space 14 space plus space 1 end cell end table

  

bold f stretchy left parenthesis 7 stretchy right parenthesis bold space bold equals bold space bold 134

b) Find straight f open parentheses x space plus space 3 close parentheses.

   

The input is x space equals space x space plus space 3 so substitute space x space plus space 3 into the expression everywhere you see an x.  

straight f open parentheses x space plus space 3 close parentheses space equals space 3 open parentheses x space plus space 3 close parentheses squared space minus space 2 open parentheses x space plus space 3 close parentheses space plus space 1  

Expand the brackets and simplify.  

table row cell straight f open parentheses x space plus space 3 close parentheses space end cell equals cell space 3 open parentheses x squared space plus space 6 x space plus space 9 close parentheses space minus space 2 open parentheses x space plus space 3 close parentheses space plus space 1 end cell row blank equals cell space 3 x squared space plus space 18 x space plus space 27 space minus space 2 x space minus space 6 space plus space 1 end cell row blank equals cell space 3 x squared space plus space 16 x space plus space 22 end cell end table  

Error converting from MathML to accessible text.

A second function is defined straight g space colon space x space rightwards arrow from bar space 3 x space – space 4.

c) Find the value of x for which straight g space colon space x space rightwards arrow from bar space minus 16.   

Form an equation by setting the function equal to -16.

 

table row cell 3 x space minus space 4 space end cell equals cell space minus 16 end cell end table

 

Solve the equation by first adding 4 to both sides, then dividing by 3. 

 

table row cell 3 x space minus space 4 space end cell equals cell space minus 16 end cell row cell 3 x space end cell equals cell space minus 12 end cell row cell x space end cell equals cell space minus 12 over 3 end cell end table

 

bold italic x bold space bold equals bold space bold minus bold 4

Domain & Range

What is the domain of a function?

  • The domain of a function is the set of values that are allowed to be the ‘input’

  • A function is only fully defined once its domain has been stated

    • If a domain is not stated then it is assumed that the domain is the largest set of possible values

      • e.g. the largest set of possible values for the function straight f open parentheses x close parentheses equals square root of x would be x greater or equal than 0

  • Restrictions on a domain can turn many-one functions into one-one functions

Restricting the domain can turn a many-one function into a one-one function

What is the range of a function?

  • The range of a function is the set of values of all possible ‘outputs’

  • The type of values in the range depend on the domain

cie-adma25-2023-domainrange-2

 

How do I find a range from a given domain?

  • The domain of a function is the set of values that are used as inputs

  • The range of a function is the set of values that are given as outputs

  • Finding the range of a function involves determining all possible output values from a given domain

    • This may need to be done by calculating each output value individually by applying the function to each input value

    • Or by considering the shape or pattern of the function 

  • To graph a function we use the inputs as the x-coordinates and the outputs as the y-coordinates

    • space f left parenthesis 2 right parenthesis equals 5 corresponds to the coordinates (2, 5)

  • Graphing the function can help you visualise the range

    • For example the range of the function straight f open parentheses x close parentheses space equals space x squared for a domain of all real values of x will be straight f open parentheses x close parentheses space greater or equal than 0 spaceas the y-coordinates on the graph are all greater than or equal to zero

Worked Example

The many-one function, straight f left parenthesis x right parenthesis, is given by

straight f open parentheses x close parentheses equals open parentheses x minus 3 close parentheses to the power of 2 space end exponent

for all values of x.

a) State the range of straight f open parentheses x close parentheses.

The 'output' from the function straight f is a squared value and so will be positive, or zero.

bold f bold space bold greater or equal than bold space bold 0

b) The domain of straight f open parentheses x close parentheses is changed to x greater than 5. Write down the changed range of straight f open parentheses x close parentheses.

As x greater than 5, straight f open parentheses x close parentheses greater than open parentheses 5 minus 3 close parentheses squared

bold therefore bold space bold f bold greater than bold 4

The Modulus Function

What is the modulus function?

  • The modulus function makes any 'input' positive

    • This is sometimes called the absolute value (of the input)

    • The modulus function is indicated by a pair of vertical lines being written around the input

      • Similar to how brackets are used

      • e.g.  vertical line 7 vertical line equals 7 comma space space space vertical line minus 7 vertical line equals 7

What is the relationship between a function and its modulus?

  • For an 'output' such that straight f open parentheses x close parentheses greater or equal than 0, then vertical line straight f open parentheses x close parentheses vertical line equals straight f open parentheses x close parentheses

    • Both the function and its modulus are positive

  • For an 'output' such that straight f open parentheses x close parentheses less than 0, then vertical line straight f open parentheses x close parentheses vertical line equals negative straight f open parentheses x close parentheses

    • The function value is negative, but its modulus is positive

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Next:Inverse Functions
    Paul

    Author: Paul

    Expertise: Maths Content Creator (Previous)

    Paul has taught mathematics for 20 years and has been an examiner for Edexcel for over a decade. GCSE, A level, pure, mechanics, statistics, discrete – if it’s in a Maths exam, Paul will know about it. Paul is a passionate fan of clear and colourful notes with fascinating diagrams.