Trigonometric Identities (Cambridge O Level Additional Maths)

Revision Note

Test yourself

Author

Amber

Last updated

12 September 2023

Did this video help you?

Simple Trig Identities

What is a trigonometric identity?

Trigonometric identities are statements that are true for all values of $x$ or $θ$
They are used to help simplify trigonometric equations before solving them
Sometimes you may see identities written with the symbol ≡
- This means 'identical to'

What trigonometric identities do I need to know?

The two trigonometric identities you must know are
- $\tan θ = \frac{\sin θ}{\cos θ}$
  - This is the identity for tan θ
  - This formula does not appear in the list of formulae
- $\sin^{2} θ + \cos^{2} θ = 1$
  - This is the Pythagorean identity
  - Note that the notation $\sin^{2} θ$ is the same as ${(\sin θ)}^{2}$
  - This formula appears in the list of formulae
Rearranging the second identity often makes it easier to work with
- $\sin^{2} θ = {1 - \cos}^{2} θ$
- $\cos^{2} θ = {1 - \sin}^{2} θ$

Where do the trigonometric identities come from?

You do not need to know the proof for these identities but it is a good idea to know where they come from
From SOHCAHTOA we know that
- $\sin θ = \frac{opposite}{hypotenuse} = \frac{O}{H}$
- $\cos θ = \frac{adjacent}{hypotenuse} = \frac{A}{H}$
- $\tan θ = \frac{opposite}{adjacent} = \frac{O}{A}$
The identity for $\tan θ$ can be seen by diving $\sin θ$ by $\cos θ$ ?
- $\frac{\sin θ}{\cos θ} = \frac{\frac{O}{H}}{\frac{A}{H}} = \frac{O}{A} = \tan θ$
This can also be seen from the unit circle by considering a right-triangle with a hypotenuse of 1
- $\tan θ = \frac{O}{A} = \frac{\sin θ}{\cos θ}$
The Pythagorean identity can be seen by considering a right-triangle with a hypotenuse of 1
- Then (opposite)²+ (adjacent)² = 1
- Therefore $\sin^{2} θ + \cos^{2} θ = 1$
Considering the equation of the unit circle also shows the Pythagorean identity
- The equation of the unit circle is $x^{2} + y^{2} = 1$
- The coordinates on the unit circle are $(\cos θ, \sin θ)$
- Therefore the equation of the unit circle could be written $\cos^{2} θ + \sin^{2} θ = 1$

How are the trigonometric identities used?

Most commonly trigonometric identities are used to change an equation into a form that allows it to be solved
They can also be used to prove further identities

Examiner Tip

If you are asked to show that one thing is identical (≡) to another, look at what parts are missing
- For example, if tan x has gone it must have been substituted

Worked example

Show that the equation $2 \sin^{2} x - \cos x = 0$ can be written in the form $a \cos^{2} x + b \cos x + c = 0$ , where $a$ , $b$ and $c$ are integers to be found.

Substitute $\sin^{2} x = 1 - \cos^{2} x$ into the equation to form a quadratic in terms of $\cos x$ .

$2 (1 - \cos^{2} x) - \cos x = 0$

Expand the bracket.

$2 - 2 \cos^{2} x - \cos x = 0$

Rewrite in the required form.

$2 \cos^{2} x + \cos x - 2 = 0$

$- 2 \cos^{2} x - \cos x + 2 = 0$

Did this video help you?

Further Trig Identities

What are the identities linking tan, sec, cot, and cosec?

Aside from the Pythagorean identity sin²x + cos²x = 1 there are two further Pythagorean identities you will need to learn

$1 + \tan^{2} θ = \sec^{2} θ$
$1 + \cot^{2} θ = {cosec}^{2} θ$
Both can be found in the list of formulae

Both of these identities can be derived from sin²x + cos²x = 1

To derive the identity for sec²x divide sin²x + cos²x = 1 by cos²x
To derive the identity for cosec²x divide sin²x + cos²x = 1 by sin²x

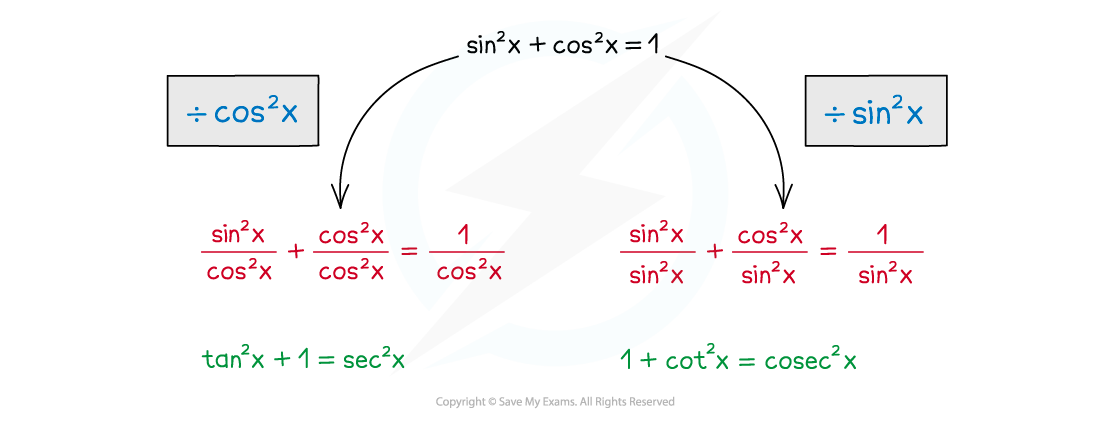
How do I prove new trigonometric identities?

You can use trigonometric identities you already know to prove new identities
To prove an identity start on one side and proceed step by step until you get to the other side
- It is more common to start on the left hand side but you can start a proof from either end
- Occasionally it is easier to show that one side subtracted from the other is zero
- You should not work on both sides simultaneously

Look for anything that could be a part of one of the above identities on either side
- For example if you see $\sin^{2} θ$ you can replace it with $1 - \cos^{2} θ$
Look for ways of reducing the number of different trigonometric functions there are within the identity
- For example if the identity contains tan θ, cot θ and cosec θ you could try
  - Using the identities tan θ = 1/cot θ and 1 + cot² θ = cosec²θ to write it all in terms of cot θ
  - Or rewriting it all in terms of sin θ and cos θ and simplifying
Often you may need to trial a few different methods before finding the correct one
Always keep an eye on the 'target' expression – this can help suggest what identities to use

Examiner Tip

Writing down all the identities you know can be a good way to spot how to get started on a question

Worked example

Solve the equation 9 sec²θ – 11 = 3 tan θ in the interval 0 ≤ θ ≤ 2π. Give your answers to three decimal places.

The squared term can be rewritten using the identity $\sec^{2} θ = 1 + \tan^{2} θ$ . Substitute this into the equation.

$9 (1 + \tan^{2} θ) - 11 = 3 \tan θ$

Rearrange to form a quadratic.

$9 + 9 \tan^{2} θ - 11 = 3 \tan θ 9 \tan^{2} θ - 3 \tan θ - 2 = 0$

Treat as a quadratic using $x = \tan θ$ .

$9 x^{2} - 3 x - 2 = 0 (3 x - 2) (3 x + 1) = 0 x = \frac{2}{3}, x = - \frac{1}{3}$

Substitute $x = \tan θ$ back in and find the principal value for each equation.

$\tan θ = \frac{2}{3} \to \tan^{- 1} (\frac{2}{3}) = 0.5880 . . . \tan θ = - \frac{1}{3} \to \tan^{- 1} (- \frac{1}{3}) = - 0.3217 . . .$

Find the other solutions in the interval by adding multiples of π.

$π + 0.5880 . . . = 3.7295 . . . π + (- 0.3217 . . .) = 2.8198 . . . 2 π + (- 0.3217 . . .) = 5.9614 . . .$

Ignore the solution that is outside the interval (-0.3217...). Round the other four to three decimal places.

$θ = 0.588, 2.820, 3.730, 5.961$

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?