Linear Graphs | Cambridge O Level Additional Maths Revision Notes 2025

Did this video help you?

Equations of a Straight Line

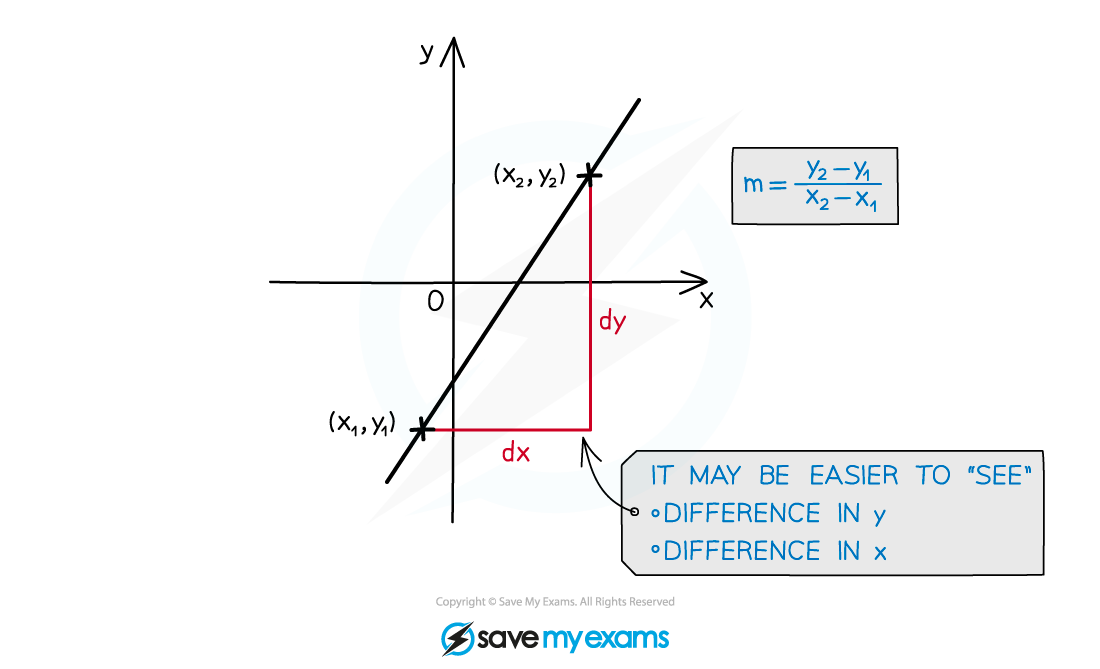
How do I find the gradient of a straight line?

Find two points that the line passes through with coordinates (x₁, y₁) and (x₂, y₂)
The gradient between these two points is calculated by

$m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$

The gradient of a straight line measures its slope
- A line with gradient 1 will go up 1 unit for every unit it goes to the right
- A line with gradient -2 will go down two units for every unit it goes to the right

Finding the gradient of a straight line graph

What are the equations of a straight line?

$y = m x + c$
- This is the gradient-intercept form
- It clearly shows the gradient m and the y-intercept (0, c)
$y - y_{1} = m (x - x_{1})$
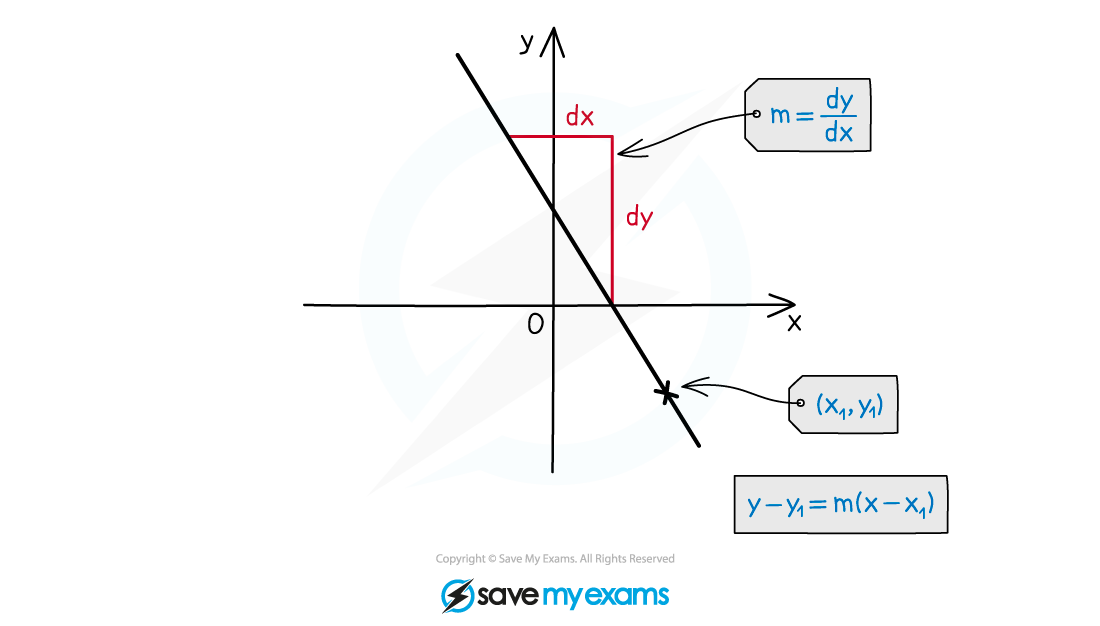
- This is the point-gradient form
- It clearly shows the gradient m and a point on the line (x₁, y₁)
$a x + b y + d = 0$
- This is the general form
- You can quickly get the x-intercept $(- \frac{d}{a}, 0)$ and y-intercept $(0, - \frac{d}{b})$

Equations of a straight line graph

How do I find an equation of a straight line?

You will need the gradient
- If you are given two points then first find the gradient
It is easiest to start with the point-gradient form
- then rearrange into whatever form is required
  - multiplying both sides by any denominators will get rid of fractions

Finding the equation of a straight line graph using the point-gradient form

Examiner Tip

Quickly sketching the graph of the straight line(s) can be helpful if you are struggling with an exam question
Ensure you state equations of straight lines in the format required
- Usually $y = m x + c$ or $a x + b y + d = 0$
- Check whether coefficients need to be integers (they usually are for $a x + b y + d = 0$ )

Worked example

(a)

Find the equation of the straight line with gradient 3 that passes through (5, 4).

We know that the gradient is 3 so the line takes the form

$y = 3 x + c$

To find the value of c, substitute (5, 4) into the equation

$4 = 3 (5) + c 4 = 15 + c c = - 11$

Replace c with −11 to complete the equation of the line

y = 3x − 11

(b)

Find the equation of the straight line that passes through (-2, 6) and (8, 1).

You may find it helpful to sketch the information given

XXg8k5ry_2-13-1-finding-equations-of-straight-lines

First find m, the gradient

\begin{array}{rcl} m & = & \frac{6 - 1}{- 2 - 8} \\ = & \frac{5}{- 10} \\ = & - \frac{1}{2} \end{array}

We know that the line takes the form

\begin{array}{rcl} y & = & - \frac{1}{2} x + c \end{array}

To find the value of c, substitute either of the given points into this equation. Here we will pick (8, 1) as it is doesn't contain negative numbers so is easier to work with

$1 = - \frac{1}{2} (8) + c 1 = - 4 + c c = 5$

Replace c with −11 to complete the equation of the line

$y = - \frac{1}{2} x + 5$

We can check against our sketch that this equation looks correct- it has a negative gradient and it crosses the y-axis between 1 and 6

Midpoint of a Straight Line

How do I find the midpoint of a line (segment)?

The midpoint of a line will be the same distance from both endpoints
You can think of a midpoint as being the average (mean) of two coordinates
The midpoint of $(x_{1}, y_{1})$ and $(x_{2}, y_{2})$ is

$(\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})$

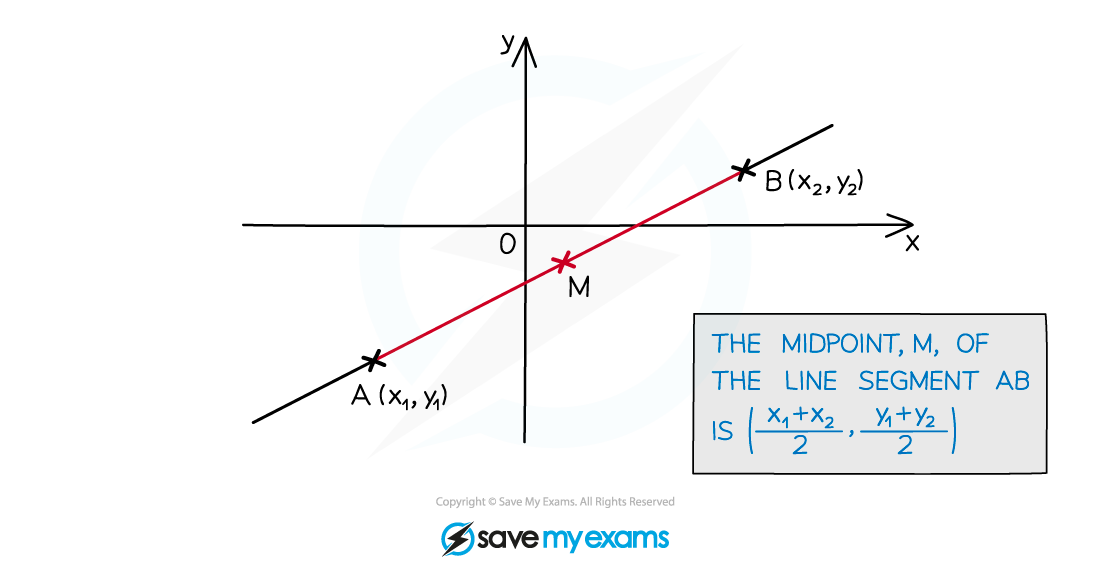
Midpoint of a line segment

M is often used as the midpoint between two points (x₁, y₁) (x₂, y₂)
It is the average of both the x and y coordinates

Worked example

The coordinates of A are (−4, 3) and the coordinates of B are (8, −12).

Find M, the midpoint of AB.

The midpoint can be found using M = $(\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})$

Fill in the values of x and y from each coordinate

$(\frac{- 4 + 8}{2}, \frac{3 + - 12}{2}) = (\frac{4}{2}, \frac{- 9}{2})$

Simplify

M = (2, −4.5)

Length of a Straight Line

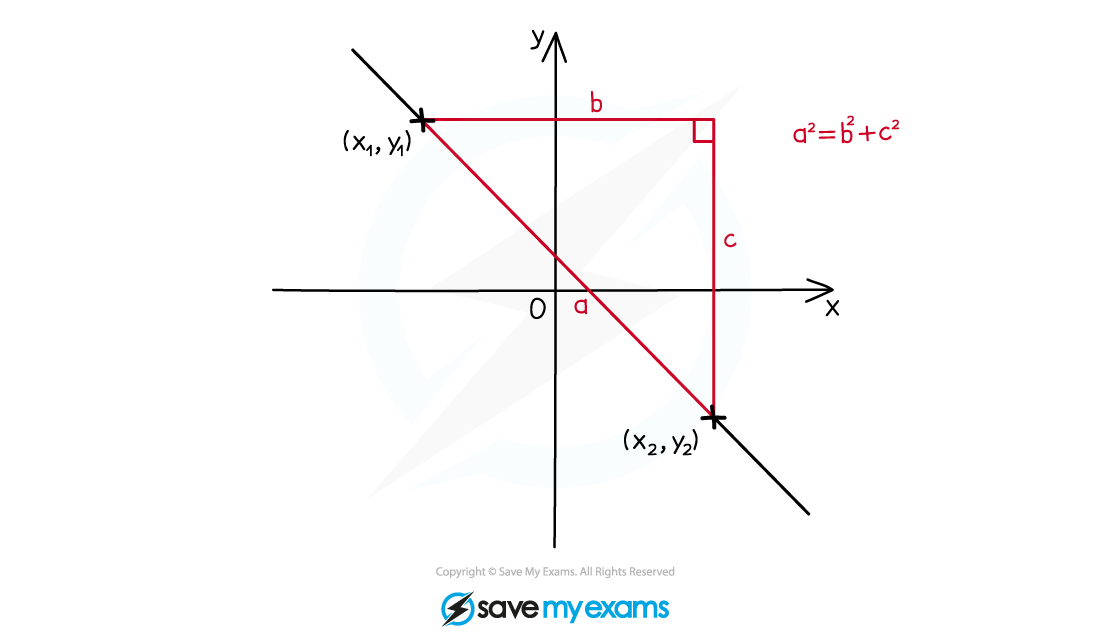
How do I calculate the length of a line?

The distance between two points with coordinates $(x_{1}, y_{1})$ and $(x_{2}, y_{2})$ can be found using the formula

$d = \sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$

This formula is really just Pythagoras’ Theorem $a^{2} = b^{2} + c^{2}$ , applied to the difference in the $x$ -coordinates and the difference in the $y$ -coordinates;

Distance between two points on a straight line graph

You may be asked to find the length of a diagonal in 3D space
- This can be answered using 3D Pythagoras

Examiner Tip

Work with the square of a distance for as long as possible as this avoids early rounding errors
- In the non-calculator paper your answer may need to be left as a surd
Only square root when forced to or for a final answer, and use the ANS button (and other memory features) on your calculator

Worked example

Point A has coordinates (3, -4) and point B has coordinates (-5, 2).

Calculate the distance of the line segment AB.

Using the formula for the distance between two points, $d = \sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$

Substituting in the two given coordinates:

$d = \sqrt{{(3 - - 5)}^{2} + {(- 4 - 2)}^{2}}$

Simplify:

$d = \sqrt{{(8)}^{2} + {(- 6)}^{2}} = \sqrt{64 + 36} = \sqrt{100} = 10$

Answer = 10 units

Linear Graphs (Cambridge O Level Additional Maths)

Revision Note

Equations of a Straight Line

How do I find the gradient of a straight line?

What are the equations of a straight line?

How do I find an equation of a straight line?

Examiner Tip

Worked example

Midpoint of a Straight Line

How do I find the midpoint of a line (segment)?

Worked example

Length of a Straight Line

How do I calculate the length of a line?

Examiner Tip

Worked example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Amber