Revision NotesExam QuestionsPast Papers
O LevelAdditional MathsCambridgeRevision NotesCoordinate GeometryCoordinate Geometry of the CircleIntersection of Two Circles

Intersection of Two Circles (Cambridge O Level Additional Maths)

Revision Note

Paul

Author

Paul

Last updated

Intersection of Two Circles

What is meant by the intersection of two circles?

  • Two circles may intersect once (touch), twice (cross), or not at all
    • Touching circles may be referred to as tangent to each other
      • they would have a common tangent line

How do I determine if two circles intersect or not?

  • Find the distance, d, between the centres of the two circles
    • This can be found using Pythagoras' theorem
      • For centres open parentheses x subscript 1 comma space y subscript 1 close parentheses and open parentheses x subscript 2 comma space y subscript 2 close parentheses, d squared equals open parentheses x subscript 2 minus x subscript 1 close parentheses squared plus open parentheses y subscript 2 minus y subscript 1 close parentheses squared
  • The radii of the two circles, r subscript 1 and r subscript 2, where r subscript 2 greater or equal than r subscript 1 are also needed
    • If r subscript 2 minus r subscript 1 less than d less than r subscript 1 plus r subscript 2 then the circles intersect twice
    •  If d equals r subscript 2 minus r subscript 1 or d equals r subscript 1 plus r subscript 2 then the circles intersect once
    • If d greater than r subscript 1 plus r subscript 2 or d less than r subscript 2 minus r subscript 1 then the circles do not intersect

The different cases for two circles intersecting

  • Rather than trying to remember those formulae, try to understand the logic behind each situation

How do I find the coordinates of the point(s) of intersection of two circles?

  • Once it has been determined that the circles do intersect at least once, the following process can be used to determine the coordinates of any intersections
  • STEP 1
    Rearrange both circle equations so that one side is zero
  • STEP 2
    Put the circle equations equal to each other (i.e. solve simultaneously!)
  • STEP 3
    Expand/rearrange/simplify into a linear equation
    • The x squared and y squared terms will cancel, leaving an equation of the form y equals m x plus c comma space x equals k or y equals k
      (These are 'diagonal line', 'vertical line' and 'horizontal line')
      The intersection(s) will lie on this line
  • STEP 4
    Substitute the linear equation into either of the circle equations
    Solving this equation will lead to either the x-coordinate(s) or y-coordinate(s) of the intersection(s)
  • STEP 5
    Substitute the x (or y) coordinates into either circle equation to find the corresponding y (or x) coordinates
    This step will not be needed in the case of the linear equation being of the form x equals k or y equals k

Examiner Tip

  • Even if not given, or asked for, a sketch of the circles can help visualise their positions relative to each other
    • You can then see if your final answers make sense with your sketch

Worked example

a)
Determine the number of intersections between the circles with equations x squared plus y squared equals 2 and open parentheses x minus 4 close parentheses squared plus y squared equals 10.

x squared plus y squared equals 2 has centre open parentheses 0 comma space 0 close parenthesesand radius square root of 2.

open parentheses x minus 4 close parentheses squared plus y squared equals 10 has centre open parentheses 4 comma space 0 close parenthesesand radius square root of 10.

table attributes columnalign right center left columnspacing 0px end attributes row cell d squared end cell equals cell open parentheses 4 minus 0 close parentheses squared plus open parentheses 0 minus 0 close parentheses squared end cell row d equals 4 end table

Using a sketch may help you to 'see' that d equals 4.

r subscript 1 equals square root of 2 comma space r subscript 2 equals square root of 10

Compare d with the sum and difference of r subscript 1 and r subscript 2.

table row cell r subscript 1 plus r subscript 2 end cell equals cell 4.576 space... end cell row cell r subscript 2 minus r subscript 1 end cell equals cell 1.748 space... end cell end table

table row cell therefore space r subscript 2 minus r subscript 1 end cell less than cell d less than r subscript 1 plus r subscript 2 end cell end table

The circles intersect twice

b)
Determine the coordinates of any intersections between the circles with equations x squared plus y squared equals 2 and open parentheses x minus 4 close parentheses squared plus y squared equals 10.

STEP 1 - Rearrange both equations so zero is on one side

table row cell x squared plus y squared minus 2 end cell equals 0 row cell open parentheses x minus 4 close parentheses squared plus y squared minus 10 end cell equals 0 end table

STEP 2 - Put the equations equal to each other

x squared plus y squared minus 2 equals open parentheses x minus 4 close parentheses squared plus y squared minus 10

STEP 3 - Expand and rearrange until in linear form

table row cell x squared plus 8 end cell equals cell x squared minus 8 x plus 16 end cell row cell 8 x minus 8 end cell equals 0 row x equals 1 end table

STEP 4 - Substitute into either circle equation

table row cell open parentheses 1 close parentheses squared plus y squared end cell equals 2 row cell y squared end cell equals 1 row y equals cell 1 comma space y equals negative 1 end cell end table

STEP 5 - Not required in this case

The intersections of the two circles have coordinates (1, 1) and (1,-1)

Equation of Common Chord

What is a common chord?

  • For circles that intersect twice the common chord is the line that joins the points of intersection
  • This line is a chord in both circles
    • Circles that intersect once (touch) have a common tangent

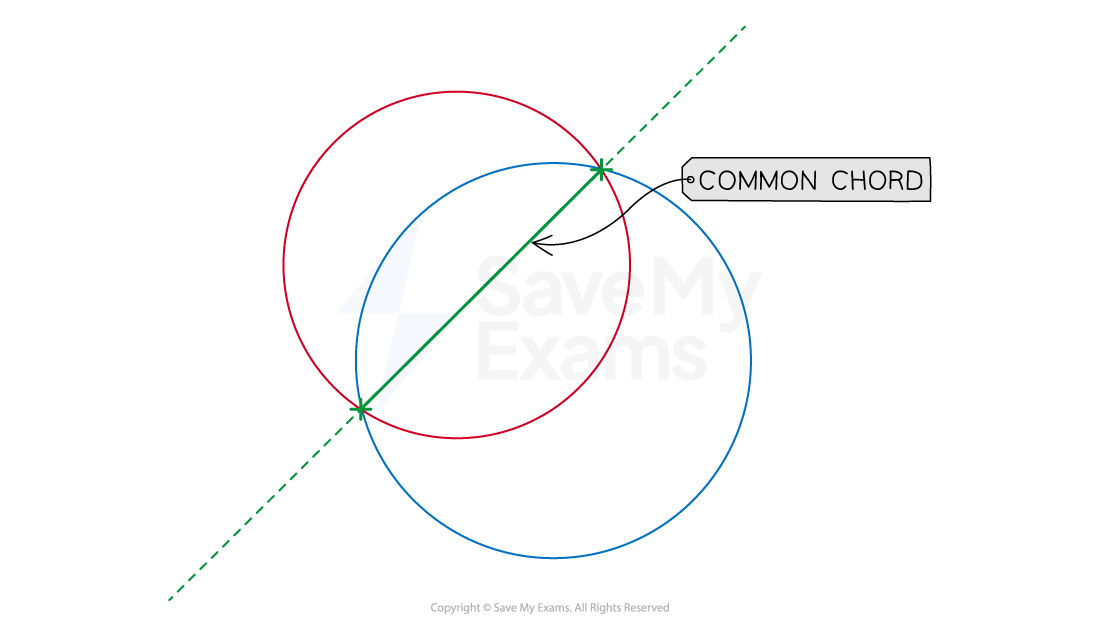
Common chord of two circles goes between the intersections

How do I find the equation of a common chord?

  • As a common chord is a straight line, its equation will be of the form y equals m x plus c unless
    • it is a horizontal line, in which case its equation will be of the form y equals k
    • it is a vertical line, in which case its equation will be of the form x equals k
  • Depending on the known information, there are two ways to find the equation of the common chord 
    • If the equations of the circles are known
      • Equate the equations and rearrange the equation into one of the three forms above
      • For example,
        x squared plus y squared minus 4 x plus 2 y minus 8 equals x squared plus y squared minus 8 x minus 2 y plus 16
        4 x plus 4 y equals 24
        So the equation of the common chord is y equals 6 minus x
    • If the points of intersection are known
      • Use the method of finding the equation of a straight line from two known points
      • If the intersection points are open parentheses x subscript 1 comma space y subscript 1 close parentheses and open parentheses x subscript 2 comma space y subscript 2 close parentheses then the equation of the common chord would be
        • y minus y subscript 1 equals fraction numerator y subscript 2 minus y subscript 1 over denominator x subscript 2 minus x subscript 1 end fraction open parentheses x minus x subscript 1 close parentheses
        • fraction numerator y subscript 2 minus y subscript 1 over denominator x subscript 2 minus x subscript 1 end fraction is the gradient and it can be easier to work this out first, separately

Worked example

Two circles intersect at the points with coordinates open parentheses 3 comma space minus 1 close parentheses and open parentheses 8 comma space 4 close parentheses.

Find the equation of the common chord of the two circles.

The points of intersection are known.
Use the method of finding the equation of a straight line from two known points.

First find the gradient,

m equals fraction numerator y subscript 2 minus y subscript 1 over denominator x subscript 2 minus x subscript 1 end fraction equals fraction numerator 4 minus open parentheses negative 1 close parentheses over denominator 8 minus 3 end fraction equals 5 over 5 equals 1

Apply y minus y subscript 1 equals m open parentheses x minus x subscript 1 close parentheses to get the equation of the common chord.

table attributes columnalign right center left columnspacing 0px end attributes row cell y minus open parentheses negative 1 close parentheses end cell equals cell 1 open parentheses x minus 3 close parentheses end cell row cell y plus 1 end cell equals cell x minus 3 end cell end table

The equation of the common chord is bold italic y bold equals bold italic x bold minus bold 4

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Tangents to CirclesNext:Radian Measure
    Paul

    Author: Paul

    Expertise: Maths

    Paul has taught mathematics for 20 years and has been an examiner for Edexcel for over a decade. GCSE, A level, pure, mechanics, statistics, discrete – if it’s in a Maths exam, Paul will know about it. Paul is a passionate fan of clear and colourful notes with fascinating diagrams – one of the many reasons he is excited to be a member of the SME team.