Definite Integrals (Cambridge (CIE) O Level Additional Maths): Revision Note
Exam code: 4037
Did this video help you?
Definite integration
What is definite integration?
Definite Integration occurs in an alternative version of the Fundamental Theorem of Calculus
This version of the Theorem is the one referred to by most textbooks/websites
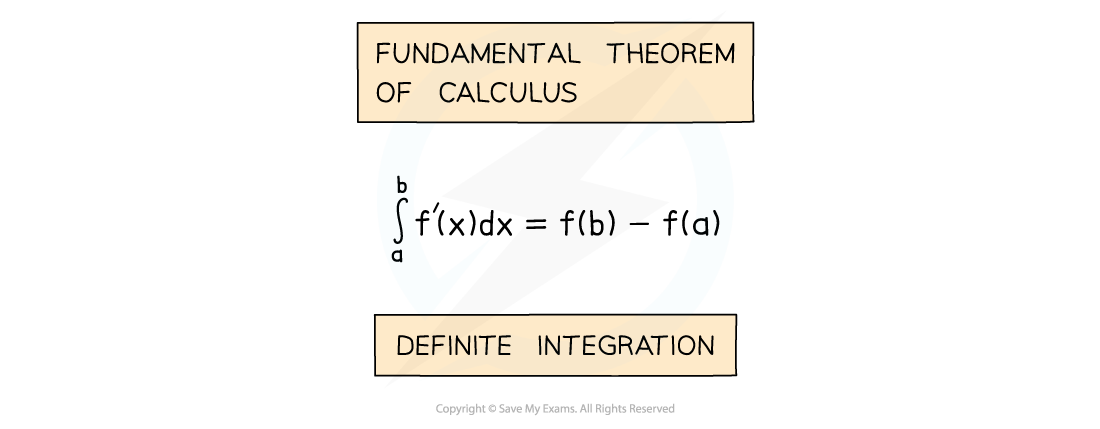
a and b are called limits
a is the lower limit
b is the upper limit
f’(x) is the derivative of f(x)
The value can be positive, zero or negative
Why do I not need to include a constant of integration for definite integration?

“+c” would appear in both f(a) and f(b)
Since we then calculate f(b) – f(a) they cancel each other out
So “+c” is not included with definite integration
How do I find a definite integral?
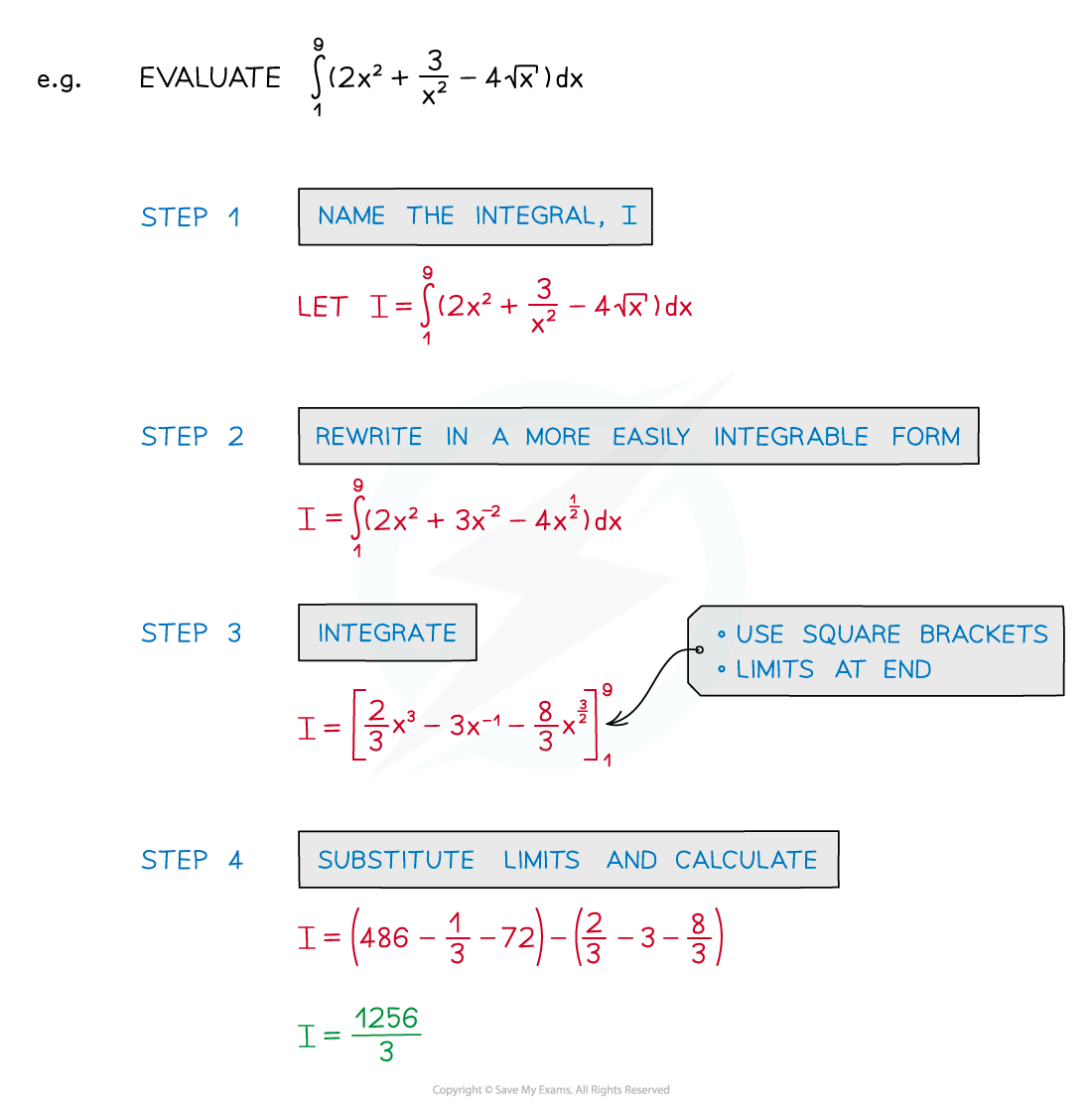
STEP 1
Give the integral a name (if it does not already have one)
This saves you having to rewrite the whole integral every time!
STEP 2
If necessary rewrite the integral into a more easily integrable form
Not all functions can be integrated directly
STEP 3
Integrate without applying the limits
Notation: use square brackets [ ] with limits placed after the end bracket
STEP 4
Substitute the limits into the function and calculate the answer
Substitute the top limit first
Then substitute the bottom limit
Subtract the second value from the first
What are the special properties of definite integrals?
Some of these have been encountered already and some may seem obvious …
taking constant factors outside the integral
where
is a constant
useful when fractional and/or negative values involved
integrating term by term
the above works for subtraction of terms/functions too
equal upper and lower limits
on evaluating, this would be a value subtracted from itself!
swapping limits gives the same, but negative, result
compare 8 subtract 5 say, with 5 subtract 8 …
splitting the interval
where
this is particularly useful for areas under multiple curves or areas under the
-axis
Examiner Tips and Tricks
Look out for questions that ask you to find an indefinite integral in one part (so “+c” needed), then in a later part use the same integral as a definite integral (where “+c” is not needed)
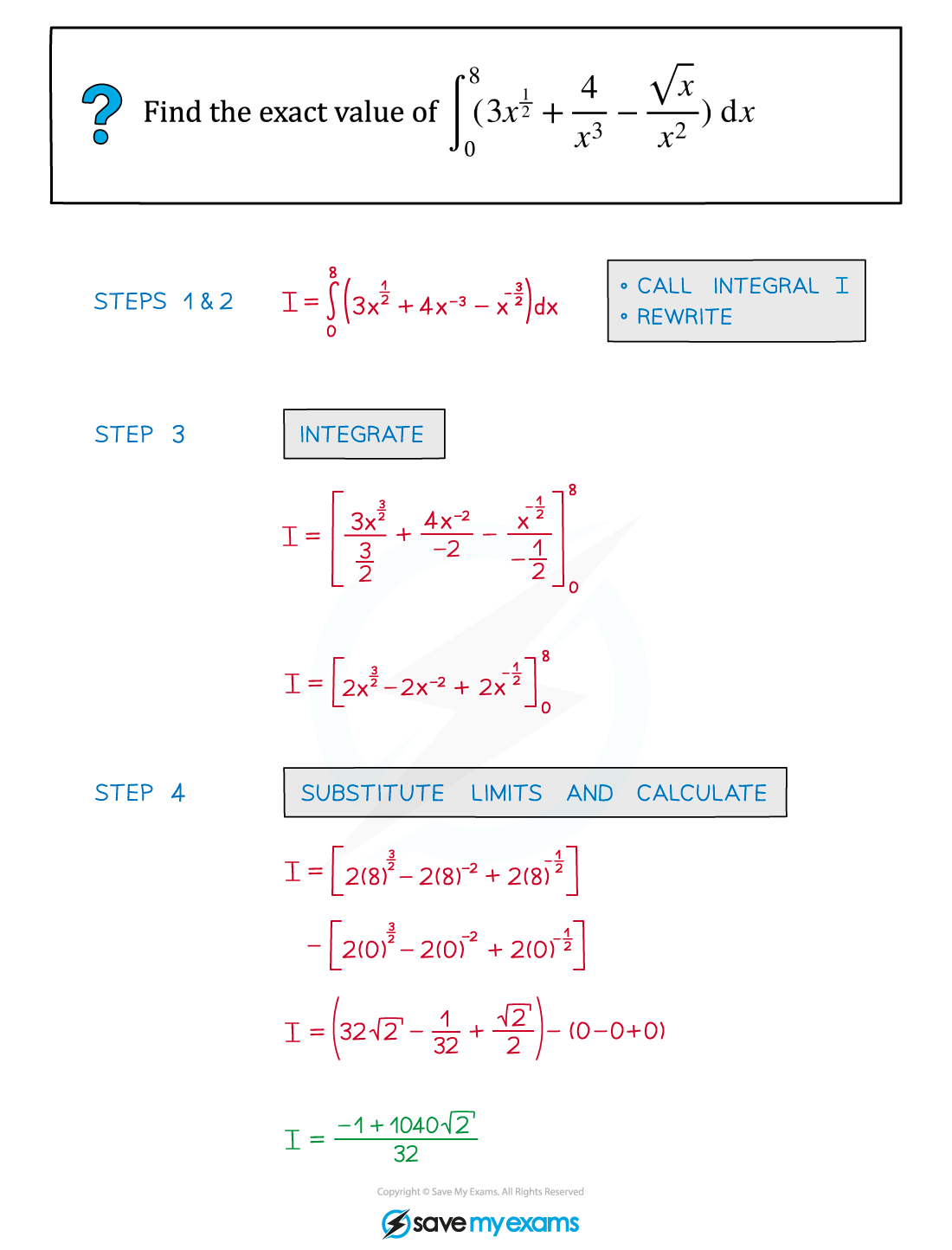
Worked Example

Unlock more, it's free!
Did this page help you?