Second Order Derivatives (Cambridge O Level Additional Maths)

Revision Note

Test yourself

Author

Amber

Last updated

13 September 2023

Did this video help you?

Second Order Derivatives

What is the second order derivative of a function?

If you differentiate the derivative of a function (i.e. differentiate the function a second time) you get the second order derivative of the function
- The second order derivative can be referred to simply as the second derivative
We can write the second derivative as $\frac{d^{2} y}{d x^{2}}$
Note the position of the powers of 2
- differentiating twice (so $d^{2}$ ) with respect to $x$ twice (so $x^{2}$ )
A first derivative is the rate of change of a function (the gradient)
- a second order derivative is the rate of change of the rate of change of a function
  - i.e. the rate of change of the function’s gradient
- A positive second derivative means the gradient is increasing
  - For instance in a u-shape, the gradient is changing from negative to positive
- A negative second derivative means the gradient is decreasing
  - For instance in an n-shape, the gradient is changing from positive to negative
Second order derivatives can be used to test whether a point is a minimum or maximum
To find a second derivative, you simply differentiate twice!
- It is important to write down your working with the correct notation, so you know what each expression means
- For example
  - $y = 5 x^{3} + 10 x^{2}$
  - $\frac{d y}{d x} = 15 x^{2} + 20 x$
  - $\frac{d^{2} y}{d x^{2}} = 30 x + 20$

Examiner Tip

Even if you think you can find the second derivative in your head and write it down, make sure you write down the first derivative as well
- If you make a mistake, you will most likely get marks for finding the first derivative

Worked example

Work out $\frac{d^{2} y}{d x^{2}}$ when

(a)

y = x^{5} - 2 x^{3} + 7 x^{2} + 9 x - 18

Find the first derivative of the function first by considering each term in turn.

$\begin{array}{rcl} \frac{d y}{d x} & = & 5 x^{4} - 6 x^{2} + 14 x + 9 \end{array}$

Find the second derivative, $\frac{d^{2} y}{d x^{2}}$ by differentiating each term in the first derivative.

$\begin{array}{rcl} \frac{d^{2} y}{d x^{2}} & = & 20 x^{3} - 12 x + 14 \end{array}$

(b)

\begin{matrix}  \end{matrix}

y = \frac{3 x + 7}{x^{4}}

To find the first derivative of the function, begin by separating the terms in the fraction.

$\begin{array}{rcl} y & = & \frac{3 x}{x^{4}} + \frac{7}{x^{4}} \end{array}$

Rewrite each term using index notation so that they are in a form that can be differentiated.

\begin{array}{rcl} y & = & 3 x (x^{- 4}) + 7 x^{- 4} = 3 x^{- 3} + 7 x^{- 4} \end{array}

Find the first derivative of the function first by differentiating each term in turn.

$\begin{array}{rcl} \frac{d y}{d x} & = & - 9 x^{- 4} - 28 x^{- 5} \end{array}$

Find the second derivative, $\frac{d^{2} y}{d x^{2}}$ by differentiating each term in the first derivative.

$\begin{array}{rcl} \frac{d^{2} y}{d x^{2}} & = & - 9 (- 4) x^{- 5} - 28 (- 5) x^{- 6} = 36 x^{- 5} + 140 x^{- 6} \end{array}$

You can turn the second derivative back into the same format as the original function by rewriting as a fraction.

$\begin{array}{rcl} \frac{d^{2} y}{d x^{2}} & = & \frac{36}{x^{5}} + \frac{140}{x^{6}} = \frac{36 x + 140}{x^{6}} \end{array}$

$\begin{array}{rcl} \frac{d^{2} y}{d x^{2}} & = & \frac{36 x + 140}{x^{6}} \end{array}$

Did this video help you?

Stationary Points & Turning Points

What are stationary points?

A stationary point is any point on a curve where the gradient is zero
To find stationary points of a curve

Step 1
Find the first derivative $\frac{d y}{d x}$

Step 2
Solve $\frac{d y}{d x} = 0$ to find the $x$ -coordinates of any stationary points

Step 3
Substitute those $x$ -coordinates into the equation of the curve to find the corresponding $y$ -coordinates

A stationary point may be either a local minimum, a local maximum, or a point of inflection

A stationary point is a local minimum, local maximum or a point of inflection

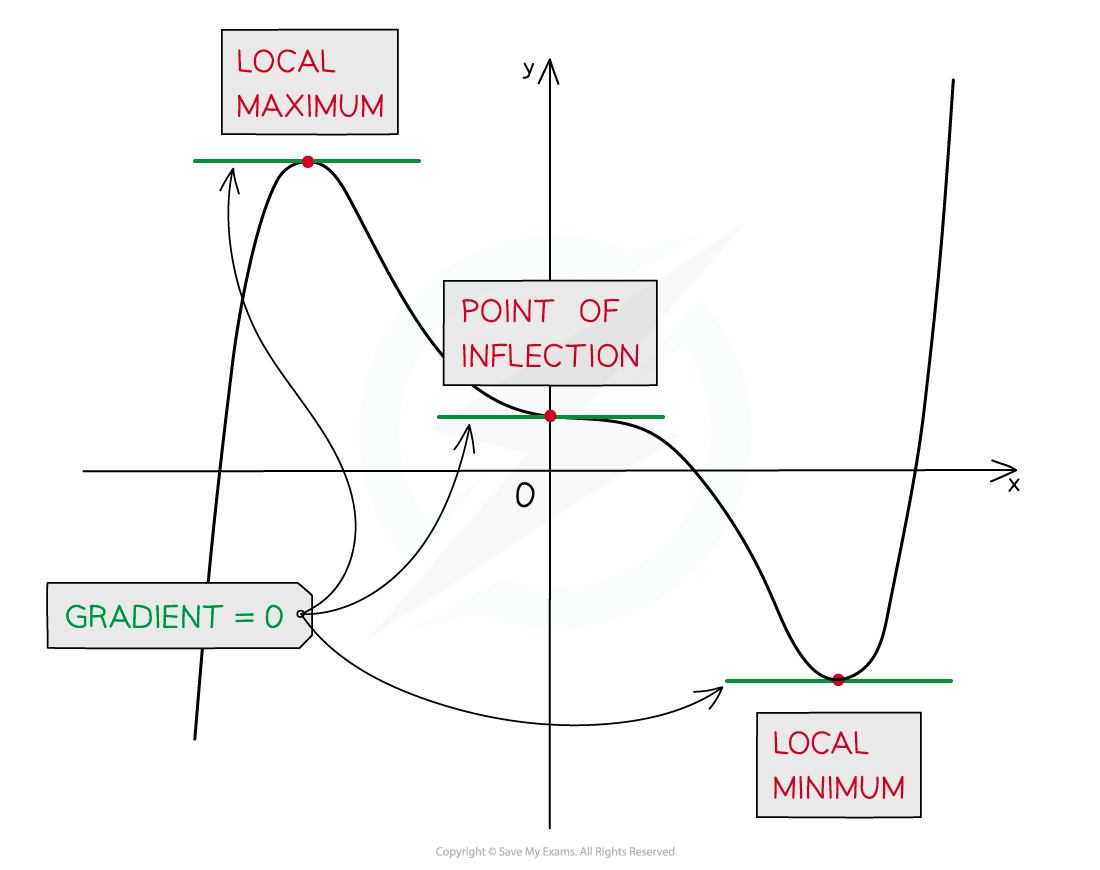
Stationary points on quadratics

The graph of a quadratic function only has a single stationary point
For a positive quadratic this is the minimum; for a negative quadratic it is the maximum
- No need to talk about 'local' here, as it is the overall minimum/maximum for the whole curve

Stationary points on quadratic graphs

The y value/coordinate of the stationary point is therefore the minimum or maximum value of the quadratic function
For quadratics especially, minimum and maximum points are often referred to as turning points

Worked example

Find the stationary point of

$y = x^{2} - 2 x$

and explain why it will be a minimum point.

Find the derivative.

$\frac{d y}{d x} = 2 x - 2$

Solve $\frac{d y}{d x} = 0$

$\begin{array}{rcl} 2 x - 2 & = & 0 \\ 2 x & = & 2 \\ x & = & 1 \end{array}$

Find the corresponding $y$ -coordinate.

$\begin{array}{rcl} x & = & 1, y = {(1)}^{2} - 2 (1) = - 1 \end{array}$

Write the answer as a coordinate.

The stationary point is (1, -1)

To explain why it is a minimum point, consider the shape of the quadratic.

(1, -1) is a minimum point because it is a positive quadratic.

Testing for Local Minimum & Maximum Points

How do I determine the nature of stationary points on a curve?

For a graph there are two ways to determine the nature of its stationary points
Method A
- Compare the signs of the first derivative, $\frac{d y}{d x}$ , (positive or negative) a little bit to either side of the stationary point
  - e.g. if the stationary point is at x=2 then you could find the gradient at x=1.9 and x=2.1

- Compare the signs (positive or negative) of the derivatives on the left and right of the stationary point
  - If the derivatives are negative on the left and positive on the right, the point is a local minimum (a u-shape)
  - If the derivatives are positive on the left and negative on the right, the point is a local maximum (an n-shape)

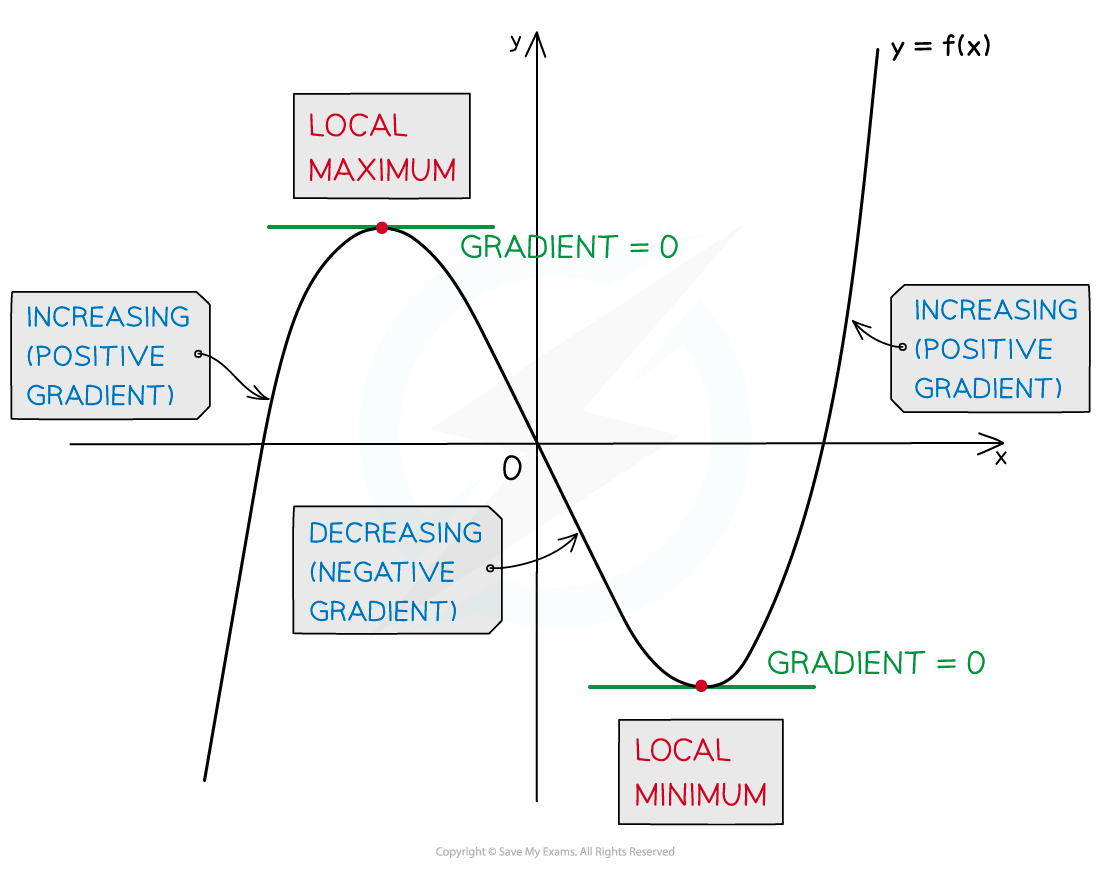
The gradient of a curve either side of a stationary point

Method B
- Look at the sign of the second derivative (positive or negative) at the stationary point
- Find the second derivative $\frac{d^{2} y}{d x^{2}}$
- For each stationary point find the value of $\frac{d^{2} y}{d x^{2}}$ at the stationary point
  - i.e. substitute the x-coordinate of the stationary point into $\frac{d^{2} y}{d x^{2}}$ and evaluate

- If $\frac{d^{2} y}{d x^{2}}$ is positive then the point is a local minimum
- If $\frac{d^{2} y}{d x^{2}}$ is negative then the point is a local maximum
- If $\frac{d^{2} y}{d x^{2}}$ is zero then the point could be a local minimum, a local maximum OR a point of inflection
  - In this case you will need to use method A instead

Examiner Tip

Usually, using the second derivative (Method B above) is a much quicker way of determining the nature of a stationary point
Sketching the curve can also help

Worked example

Find the stationary points of

$y = x^{2} (2 x^{2} - 4)$

and determine the nature of each.

Start by expanding the brackets in the expression for $y$

$y = 2 x^{4} - 4 x^{2}$

Step 1
Find the first derivative

$\frac{d y}{d x} = 8 x^{3} - 8 x$

Step 2
Solve $\frac{d y}{d x} = 0$

$\begin{array}{rcl} 8 x^{3} - 8 x & = & 0 \end{array}$

Divide through by 8

$\begin{array}{rcl} x^{3} - x & = & 0 \end{array}$

Fully factorise, spotting the difference of two squares

$\begin{array}{rcl} x (x^{2} - 1) & = & 0 \\ x (x - 1) (x + 1) & = & 0 \end{array}$

Solve to find the $x$ -coordinates of the stationary (turning) points

$x_{1} = 0, x_{2} = 1, x_{3} = - 1$

Step 3
Find the corresponding $y$ -coordinates

$\begin{array}{rcl} x_{1} & = & 0, y_{1} = {(0)}^{2} (2 {(0)}^{2} - 4) = 0 \\ x_{2} & = & 1, y_{2} = {(1)}^{2} (2 {(1)}^{2} - 4) = - 2 \\ x_{3} & = & - 1, y_{3} = {(- 1)}^{2} (2 {(- 1)}^{2} - 4) = - 2 \end{array}$

Write the answers as coordinates, being careful to correctly match $x$ 's and $y$ 's

The stationary points are (0, 0), (1, -2) and (-1, -2)

To find the nature of each stationary point, use Method B
Step 4
Find the second derivative

$\frac{d^{2} y}{d x^{2}} = 24 x^{2} - 8$

Step 5
Evaluate the second derivative at each stationary point

$\begin{array}{rcl} x & = & 0, \frac{d^{2} y}{d x^{2}} = 24 {(0)}^{2} - 8 = - 8 (< 0) \\ x & = & 1, \frac{d^{2} y}{d x^{2}} = 24 {(1)}^{2} - 8 = 16 (> 0) \\ x & = & - 1, \frac{d^{2} y}{d x^{2}} = 24 {(- 1)}^{2} - 8 = 16 (> 0) \end{array}$

The nature of each stationary point is now determined

(0, 0) is a local minimum point
(1, -2) is a local minimum point
(-1, -2) is a local minimum point

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?

Second Order Derivatives (Cambridge O Level Additional Maths)

Revision Note

What is the second order derivative of a function?

What are stationary points?

Stationary points on quadratics

How do I determine the nature of stationary points on a curve?

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Amber