Quotient Rule (Cambridge O Level Additional Maths)

What is the quotient rule?

• The quotient rule is a formula that allows you to differentiate a quotient of two functions
  • i.e. one function divided by another
• If where u and v are functions of x then the quotient rule is:

• In function notation, if then the quotient rule can be written as:

• As with the product rule, ‘dash notation’ may be used to make remembering it easier

• Final answers should match the notation used throughout the question

How do I know when to use the quotient rule?

• The quotient rule is used when trying to differentiate a fraction where both the numerator and denominator are functions of
  • if the numerator is a constant, negative powers can be used
  • if the denominator is a constant, treat it as a factor of the expression\

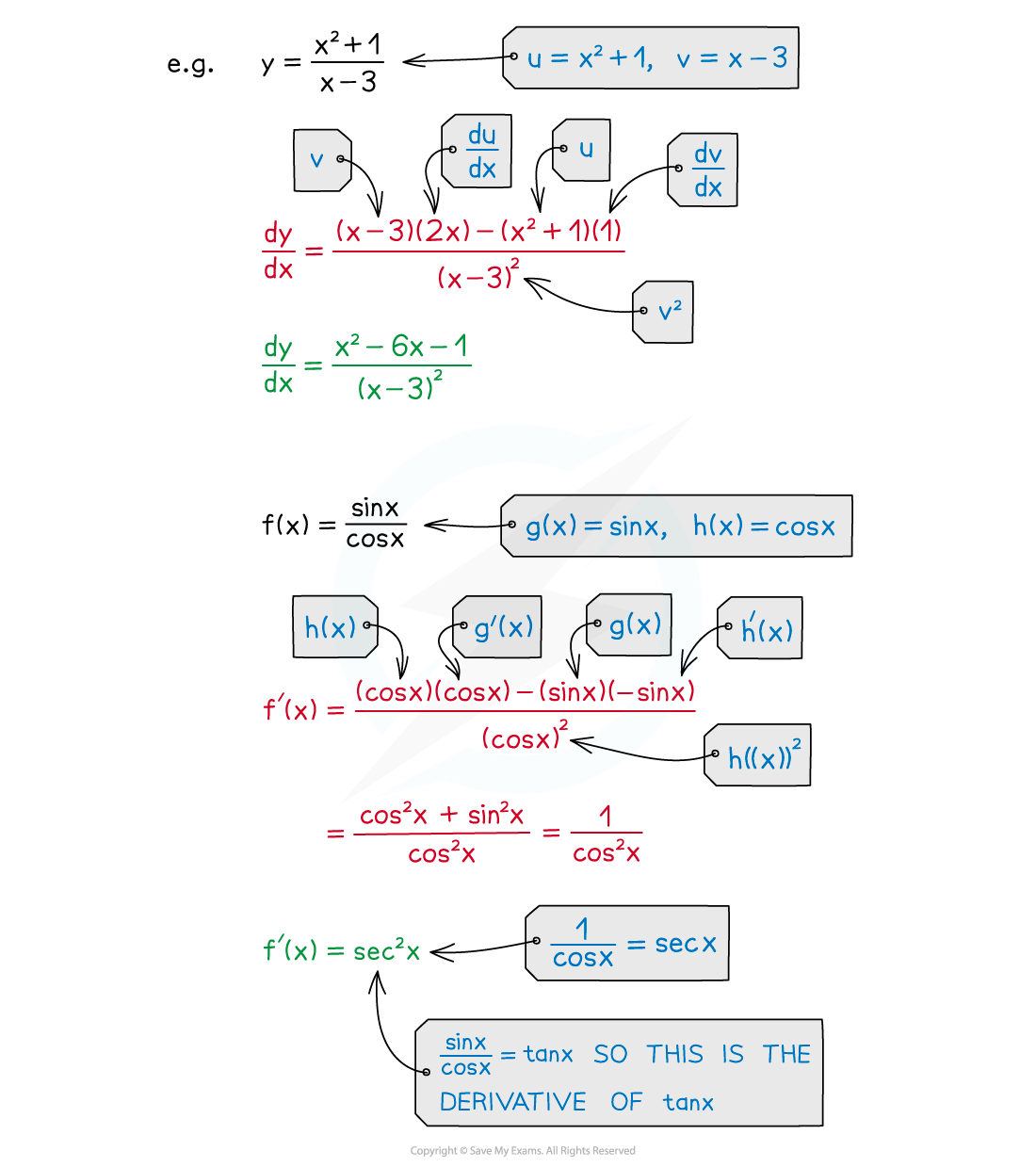
How do I use the quotient rule?

• Make it clear what and are
  • arranging them in a square can help
    • opposite diagonals match up (like they do for product rule)

 Identify the two functions, and

 Differentiate both and with respect to to find and

Obtain  by applying the quotient rule formula

Be careful using the formula – because of the minus sign in the numerator, the order of the functions is important

Simplify the answer if straightforward or if the question requires a particular form