O LevelAdditional MathsCambridgeRevision NotesCalculusCalculus for KinematicsKinematics Toolkit

Kinematics Toolkit (Cambridge O Level Additional Maths)

Revision Note

Test yourself
Paul

Author

Paul

Last updated

Displacement, Velocity & Acceleration

What is kinematics?

  • Kinematics is the branch of mathematics that models and analyses the motion of objects
  • Common words such as distance, speed and acceleration are used in kinematics but are used according to their technical definition

What definitions do I need to be aware of?

  • Firstly, only motion of an object in a straight line is considered
    • this could be a horizontal straight line
      • the positive direction would be to the right
    • or this could be a vertical straight line
      • the positive direction would be upwards
  • Particle
    • A particle is the general term for an object
    • some questions may use a specific object such as a car or a ball
  • Time space t seconds
    • Displacement, velocity and acceleration are all functions of timespace t
    • Initially time is zero t equals 0
  • Displacement space s m
    • The displacement of a particle is its distance relative to a fixed point
    • the fixed point is often (but not always) the particle’s initial position
    • Displacement will be zero s equals 0 if the object is at or has returned to its initial position
    • Displacement will be negative if its position relative to the fixed point is in the negative direction (left or down)
  • Distance space d m
    • Use of the word distance needs to be considered carefully and could refer to
      • the distance travelled by a particle
      • the (straight line) distance the particle is from a particular point
    • Be careful not to confuse displacement with distance
    • if a bus route starts and ends at a bus depot, when the bus has returned to the depot, its displacement will be zero but the distance the bus has travelled will be the length of the route
    • Distance is always positive
  • Velocity space vm s-1
    • The velocity of a particle is the rate of change of its displacement at timespace t
    • Velocity will be negative if the particle is moving in the negative direction
    • A velocity of zero means the particle is stationary v equals 0
  • Speed space open vertical bar v close vertical bar m s-1
    • Speed is the magnitude (a.k.a. absolute value or modulus) of velocity
    • as the particle is moving in a straight line, speed is the velocity ignoring the direction
      • ifspace v equals 4 comma space open vertical bar v close vertical bar equals 4
      • ifspace v equals negative 6 comma space open vertical bar v close vertical bar equals 6
  • Acceleration space a m s-2
    • The acceleration of a particle is the rate of change of its velocity at timespace t
    • Acceleration can be negative but this alone cannot fully describe the particle’s motion
      • if velocity and acceleration have the same sign the particle is accelerating (speeding up)
      • if velocity and acceleration have different signs then the particle is decelerating (slowing down)
      • if acceleration is zero a equals 0 the particle is moving with constant velocity 
      • in all cases the direction of motion is determined by the sign of velocity

Are there any other words or phrases in kinematics I should know?

  • Certain words and phrases can imply values or directions in kinematics
    • a particle described as “at rest” means that its velocity is zero,bold space bold italic v bold equals bold 0
    • a particle described as moving “due east” or “right” or would be moving in the positive horizontal direction
      • this also means thatbold space bold italic v bold greater than bold 0
    • a particle “dropped from the top of a cliff” or “down” would be moving in the negative vertical direction
      • this also means thatbold space bold italic v bold less than bold 0

What are the key features of a velocity-time graph?

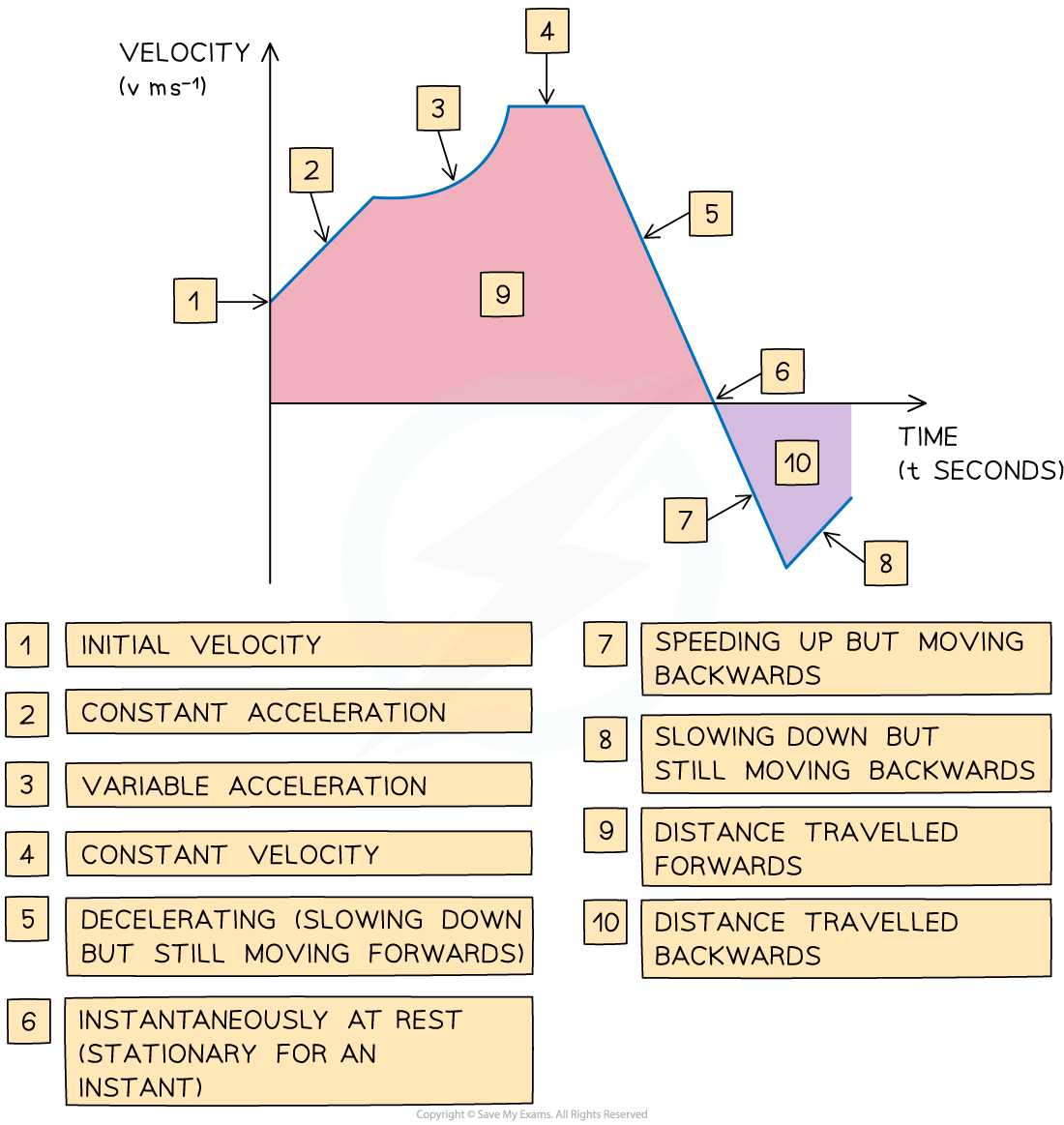
  • The gradient of the graph equals the acceleration  of an object
  • A straight line shows that the object is accelerating at a constant rate
  • A horizontal line shows that the object is moving at a constant velocity
    • Graph above the x-axis means the object is moving forwards
    • Graph below the x-axis means the object is moving backwardsThe area between graph and the x-axis tells us the change in displacement of the object
  • The total displacement of the object from its starting point is the sum of the areas above the x-axis minus the sum of the areas below the x-axis
  • The total distance travelled by the object is the sum of all the areas
  • If the graph touches the x-axis then the object is stationary at that time
  • If the graph is above the x-axis then the object has positive velocity and is travelling forwards
  • If the graph is below the x-axis then the object has negative velocity and is travelling backwards

velocity time graph with different sections labelled and described

Examiner Tip

  • In an exam if you are given an expression for the velocity then sketching a velocity-time graph can help visualise the problem

Worked example

A particle is projected vertically upwards from ground level, taking 8 seconds to return to the ground.

The velocity-time graph below illustrates the motion of the particle for these 8 seconds.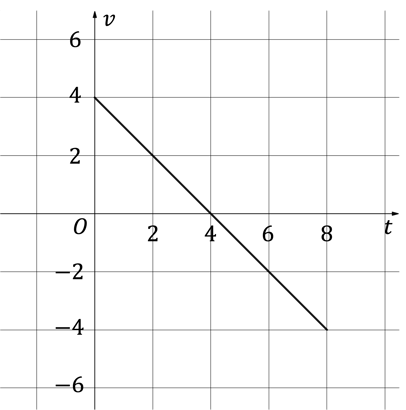velocity time graph with negative gradient

i)
How many seconds does the particle take to reach its maximum height?
Give a reason for your answer.
ii)
State, with a reason, whether the particle is accelerating or decelerating at timespace t equals 3.

 

i)
At maximum height, velocity is zero.
 
v equals 0 at t equals 4
 
The particle takes 4 seconds to reach its maximum height.
This is because its velocity is 0 ms-1 at 4 seconds.
  
ii)
At t equals 3, velocity is positive
 
Acceleration is the gradient of velocity.
 
At t equals 3, acceleration is negative
 
At 3 seconds the particle is decelerating as its velocity and acceleration have different signs.

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfNext topic

    Did this page help you?

    Paul

    Author: Paul

    Expertise: Maths

    Paul has taught mathematics for 20 years and has been an examiner for Edexcel for over a decade. GCSE, A level, pure, mechanics, statistics, discrete – if it’s in a Maths exam, Paul will know about it. Paul is a passionate fan of clear and colourful notes with fascinating diagrams – one of the many reasons he is excited to be a member of the SME team.