Quadratic Graphs

A quadratic is a function of the form $y = a x^{2} + b x + c$ where $a$ is not zero
They are a very common type of function in mathematics, so it is important to know their key features

What does a quadratic graph look like?

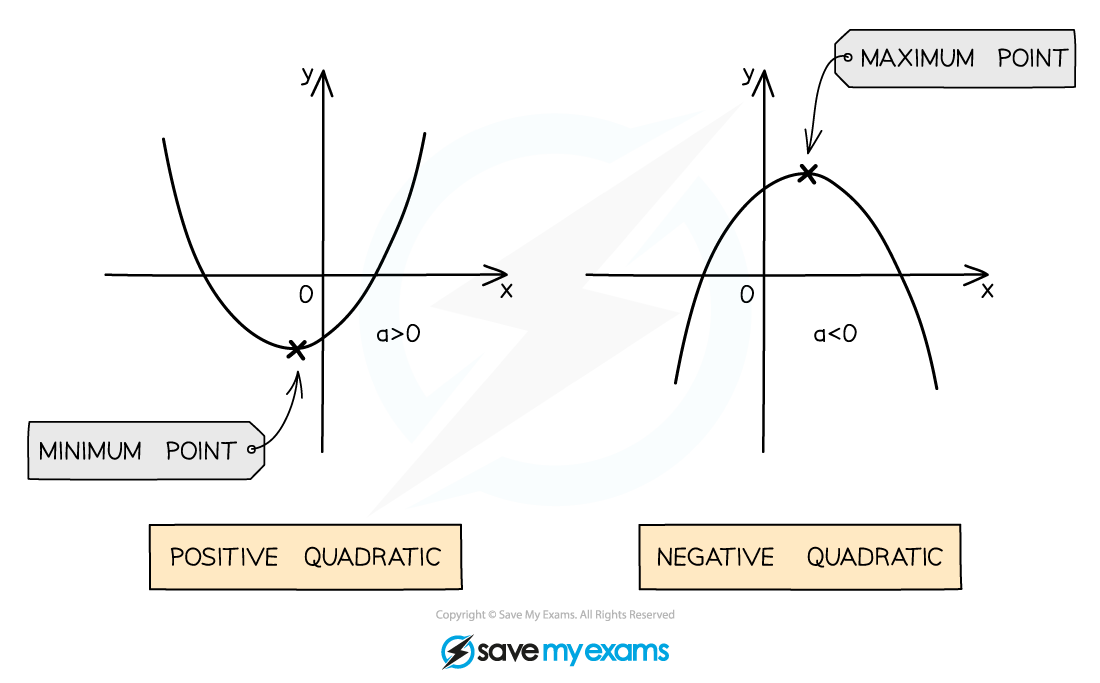
The shape made by a quadratic graph is known as a parabola
The parabola shape of a quadratic graph can either look like a “∪-shape” or a “∩-shape”
- A quadratic with a positive coefficient of $x^{2}$ will be a ∪-shape
- A quadratic with a negative coefficient of $x^{2}$ will be a ∩-shape
A quadratic will always cross the $y$ -axis
A quadratic may cross the $x$ -axis twice, once, or not at all
- The points where the graph crosses the $x$ -axis are called the roots
If the quadratic is a ∪-shape, it has a minimum point (the bottom of the ∪)
If the quadratic is a ∩-shape, it has a maximum point (the top of the ∩)
Minimum and maximum points are both examples of turning points

Two quadratics: one positive and one negative

How do I sketch a quadratic graph?

We could create a table of values for the function and then plot it accurately
- However we often only require a sketch to be drawn, showing just the key features
The key features needed to be able to sketch a quadratic graph are
- the overall shape
  - ∪-shape graphs occur when $a > 0$ (positive quadratic)
  - ∩-shape graphs occur when $a < 0$ (negative quadratic)
- the $x$ -intercept(s), these are also known as the roots (there may be none!)
  - roots are found by setting the quadratic function (or $y$ ) equal to zero
  - i.e. solve $a x^{2} + b x + c = 0$
  - if there are no (real) solutions (i.e. no roots), the graph does not intersect the $x$ -axis
    - the discriminant can be used to determine whether a quadratic function has 0, 1 or 2 roots
- the $y$ -intercept
  - this is found by setting $x = 0$ in the quadratic function
  - so for $a x^{2} + b x + c$ the coordinates of the $y$ -intercept will be $(0, c)$
- the minimum or maximum point (turning point)
  - sometimes a rough idea of where this should lie is enough
  - sometimes the specific coordinates of the turning point will be needed
  - when required the coordinates of the turning point can be found by either completing the square or differentiation
    - in cases where the quadratic has just one root, the graph will touch (rather than cross) the $x$ -axis and so this will be the turning point

Worked example

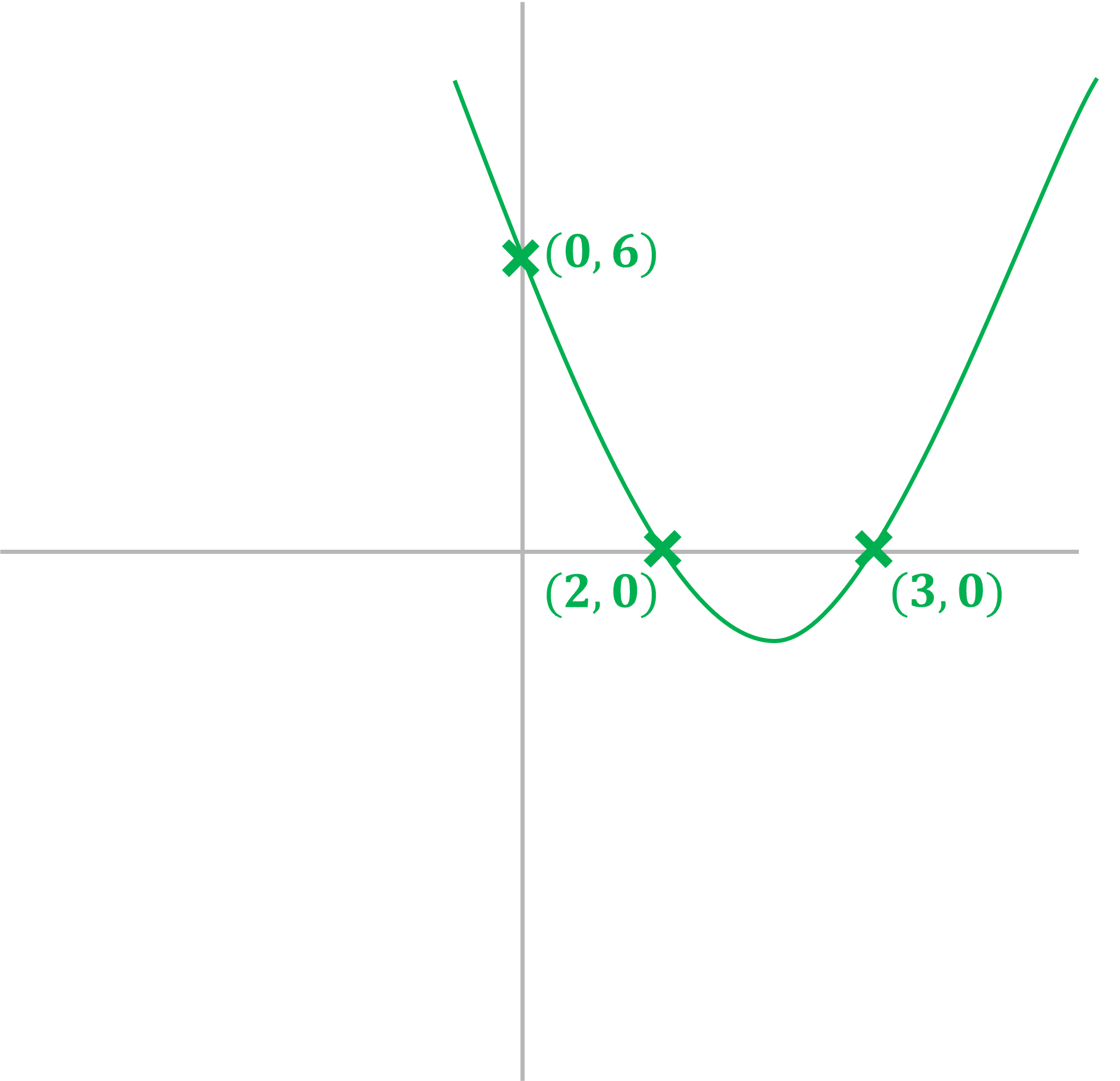
Sketch the graph of $y = x^{2} - 5 x + 6$ , labelling any intercepts with the coordinate axes.

It is a positive quadratic, so will be a $\cup$ -shape

The ' $+ c$ ' at the end is the $y$ -intercept ( $y = c$ when $x = 0$ ), so the graph crosses the $y$ -axis at (0,6)

Factorise

$y = (x - 2) (x - 3)$

Solve $y = 0$

$(x - 2) (x - 3) = 0$

$x = 2 or x = 3$

So the roots of the graph are

(2,0) and (3,0)

cie-igcse-quadratic-graphs-we-1

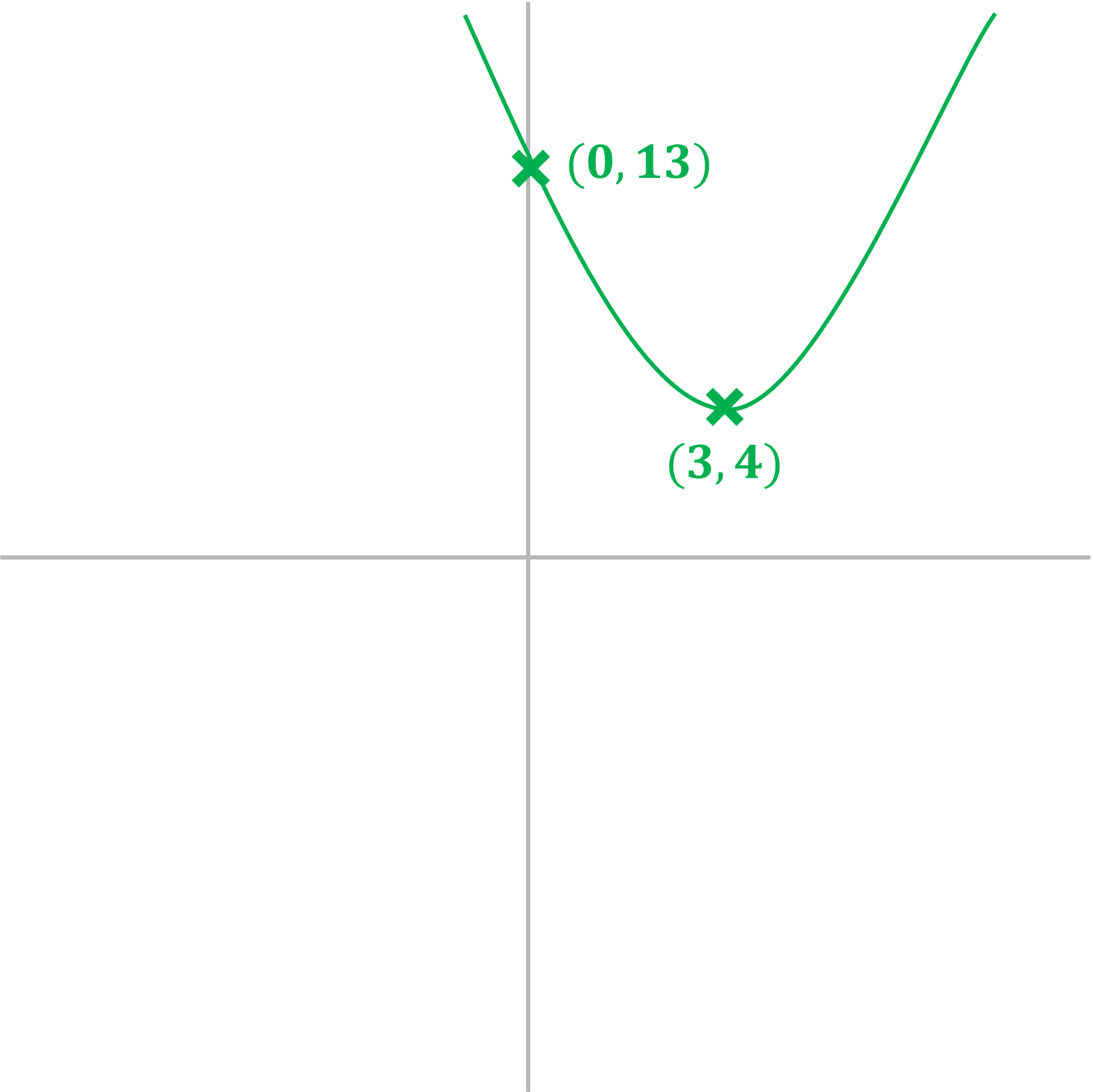
Sketch the graph of $y = x^{2} - 6 x + 13$ , labelling any intercepts with the coordinate axes.

It is a positive quadratic, so will be a $\cup$ -shape

The ' $+ c$ ' at the end is the $y$ -intercept, so this graph crosses the y-axis at

(0,13)

The discriminant of the quadratic is ' $b^{2} - 4 a c$ '

${(- 6)}^{2} - 4 (1) (13) = 36 - 52 = - 16$

As the discriminant is negative, there are no (real) roots and the graph does not intersect the $x$ -axis

(Note we have included the coordinates of the turning point, $(3, 4)$ to help you visualise the graph, but there was no requirement from the question to do this - on a sketch like this, the turning point should be in the correct quadrant)

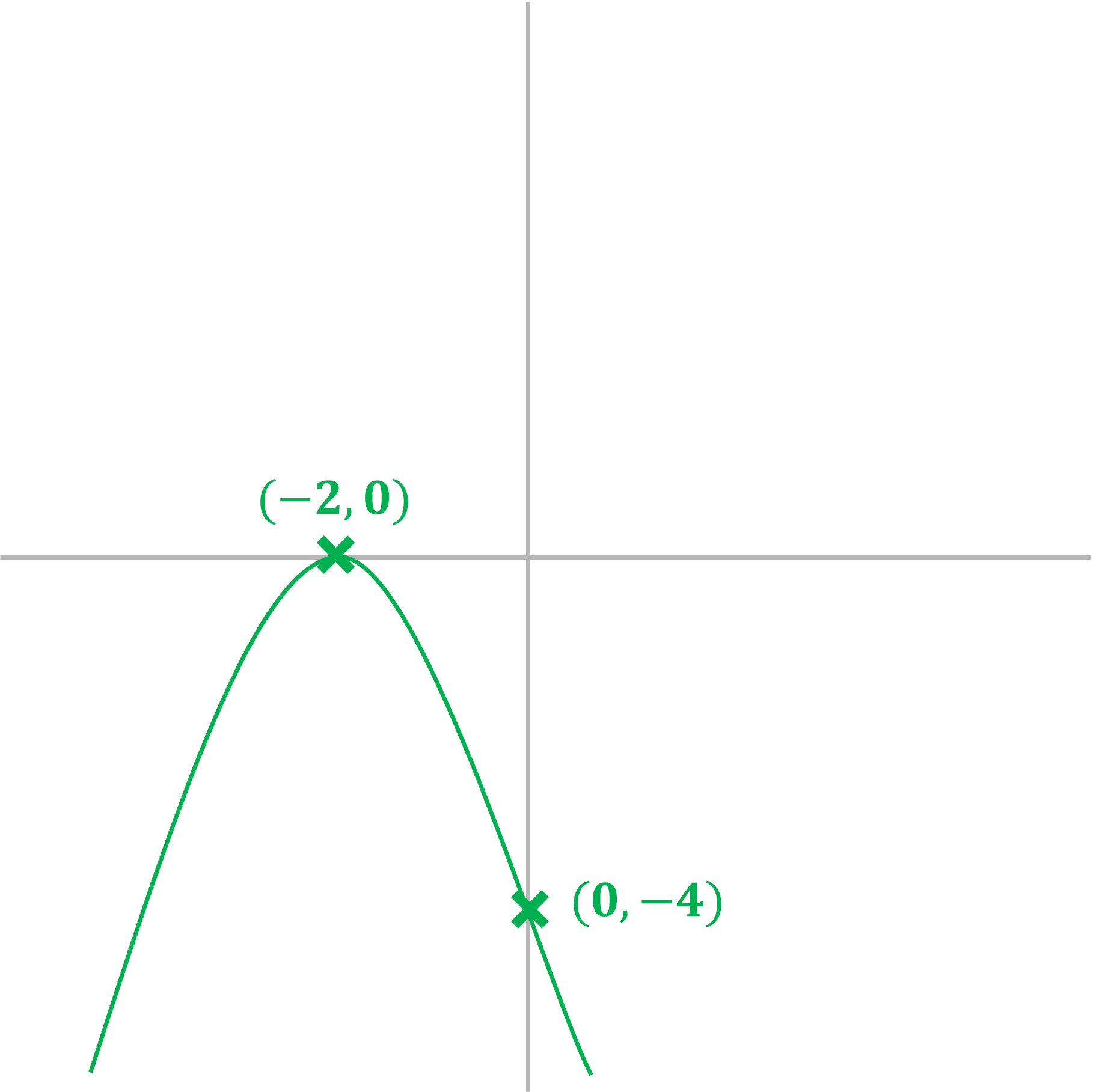
cie-igcse-quadratic-graphs-we-2

Sketch the graph of $y = - x^{2} - 4 x - 4$ , labelling any intercepts with the coordinate axes and the turning point.

It is a negative quadratic, so will be an $\cap$ -shape

The ' $+ c$ ' at the end is the $y$ -intercept, so this graph crosses the $y$ -axis at (0, -4)

Factorising

$- x^{2} - 4 x - 4 = - (x^{2} + 4 x + 4) = - {(x + 2)}^{2}$

This shows that there is only one root and the graph will touch the $x$ -axis at the point (-2, 0)
This point will also be the turning point - and as this is a negative quadratic - will be a maximum point

cie-igcse-quadratic-graphs-we-3

Sketching Graphs by Completing the Square

How does completing the square help me sketch graphs?

Completing the square can quickly tell us the coordinates of the turning point on a quadratic graph
This is based on the fact that a squared term (e.g. ${(x + 1)}^{2}$ ) cannot be negative
STEP 1
Complete the square - rewrite $a x^{2} + b x + c = 0$ in the form $a {(x + p)}^{2} + q$
STEP 2
Deduce the $x$ -coordinate of the turning point
- ${(x + p)}^{2} \geq 0$ for all values of $x$
- Therefore it's minimum value is 0, and this occurs when $x = - p$

The $x$ -coordinate is $- p$

STEP 3
Deduce the $y$ -coordinate of the turning point
- $a {(x + p)}^{2} = 0$
- Therefore $y = q$

The $y$ -coordinate is $q$

STEP 4
The turning point has coordinates $(- p, q)$
This can be considered when sketching the graph of the quadratic function
Note that the turning point could be a maximum or minimum point - this will depend on the value of $a$
- $a$ is the coefficient of the $x^{2}$ term
- If $a$ is positive, the graph is $\cup$ - shaped and will have a minimum point
- If $a$ is negative, the graph is $\cap$ - shaped and will have a maximum point

How do I use the graph of a quadratic function to find its range?

The range of a quadratic function will be shown on its graph by the values $y$ takes
- i.e. the turning point from a quadratic graph will determine its range
For the quadratic function $f (x)$ whose graph has a minimum point $(x_{m i n}, y_{m i n})$
- the range of the $f (x)$ will be $f \geq y_{m i n}$
For the quadratic function $f (x)$ whose graph has a maximum point $(x_{m a x}, y_{m a x})$
- the range of $f (x)$ will be $f \leq y_{m a x}$
If there any restrictions on the domain of $f (x)$ then they could affect the range of $f (x)$

Worked example

Sketch the graph of $y = f (x)$ where $f (x) = 2 x^{2} - 4 x - 6$ , giving the coordinates of the turning point, and any points where the graph intercepts the coordinate axes. Use your graph to write down the range of $f (x)$ .

STEP 1 - Complete the square.

$\begin{array}{rcl} f (x) & = & 2 (x^{2} - 2 x) - 6 \\ = & 2 [{(x - 1)}^{2} - 1] - 6 \\ = & 2 {(x - 1)}^{2} - 8 \end{array}$

STEP 2 - Deduce the $x$ -coordinate.

$x = - (- 1) = 1$

STEP 3 - Deduce the $y$ -coordinate.

$y = - 8$

STEP 4 - Label the turning point when sketching the graph of the quadratic function.

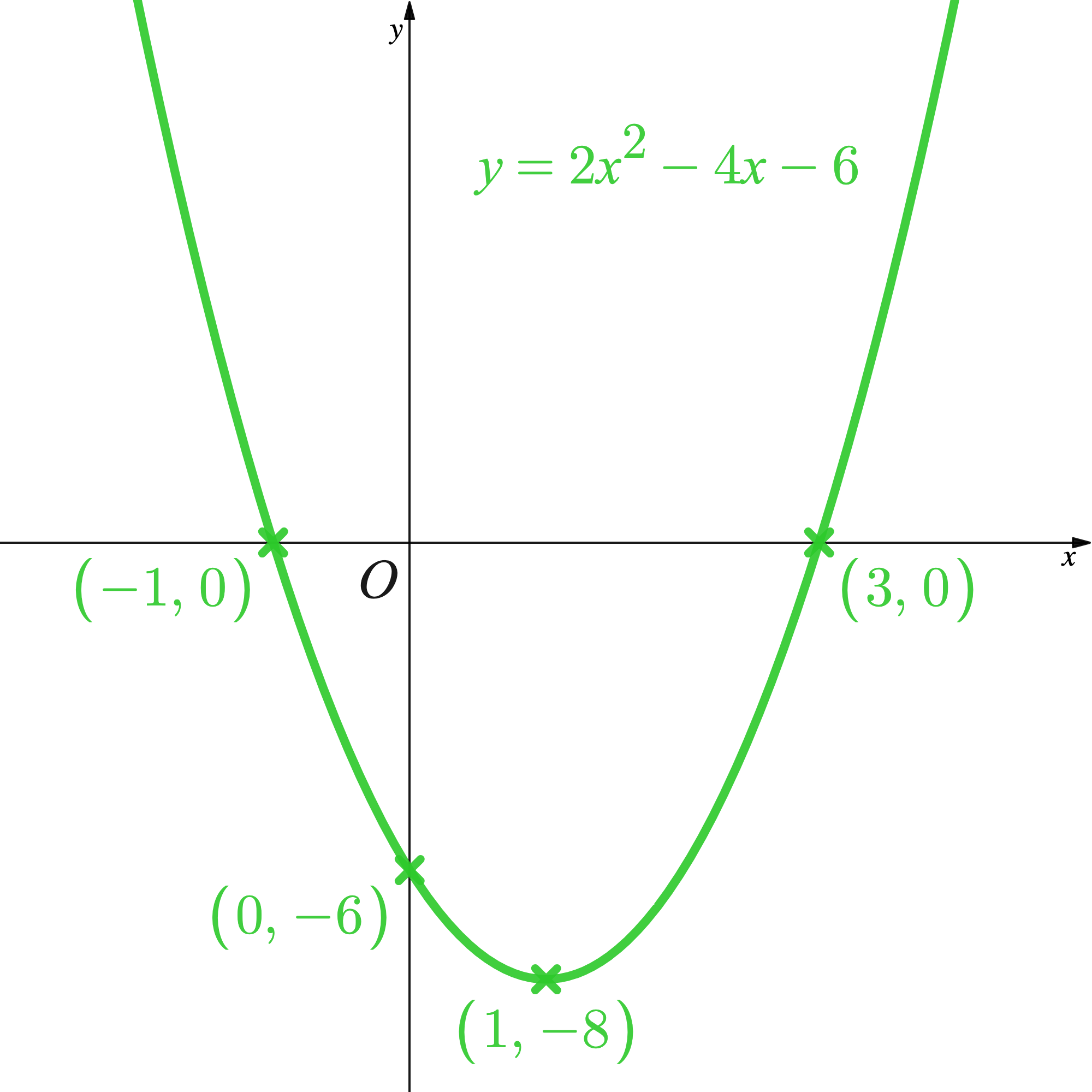
desmos-graph-8

The graph has a minimum point so the range will be greater than or equal to the $y$ -coordinate of this point.

The range of $f (x)$ is $f > - 8$

Quadratic Graphs (Cambridge O Level Additional Maths)

Revision Note