Exponential Functions (Cambridge O Level Additional Maths)

What is an exponential function?

• An exponential functions in a function where the variable is the power
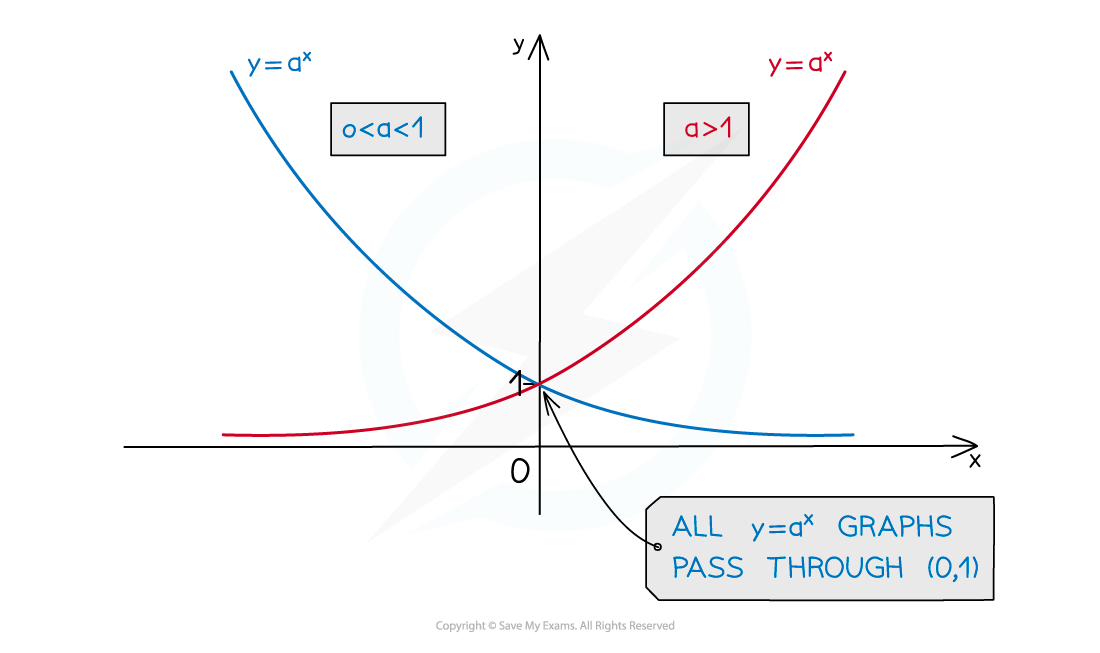
• They are of the form y = a^x with a > 0 

What is an exponential graph?

• All graphs of the form y = a^x will pass through (0, 1) because a⁰ = 1
• The x-axis is an asymptote

Exponential graphs when a > 1

• Where x < 0 the higher value of a is the “lower” graph
• Where x > 0 the higher value of a is the “higher” graph
• a > 1 is exponential growth 

What about when a ≤ 1?

• You may like to think about why a = 1 is not considered... If a = 1, y = 1^x = 1 for all values of x
• 0 < a < 1 represents exponential decay
  • Where x < 0 the higher value of a is the “higher” graph
  • Where x > 0 the higher value of a is the “lower” graph

  

What is e, the exponential function?

• The exponential function is y = e^x
  • e is an irrational number
  • e ≈ 2.718
• As with other exponential graphs y = e^x
  • passes through (0, 1)
  • has the x-axis as an asymptote

  

What is the big deal with e?

• y = e^x has the particular property

• i.e. for every real number x, the gradient of y = e^x is also equal to e^x (see Differentiating e^x and lnx)

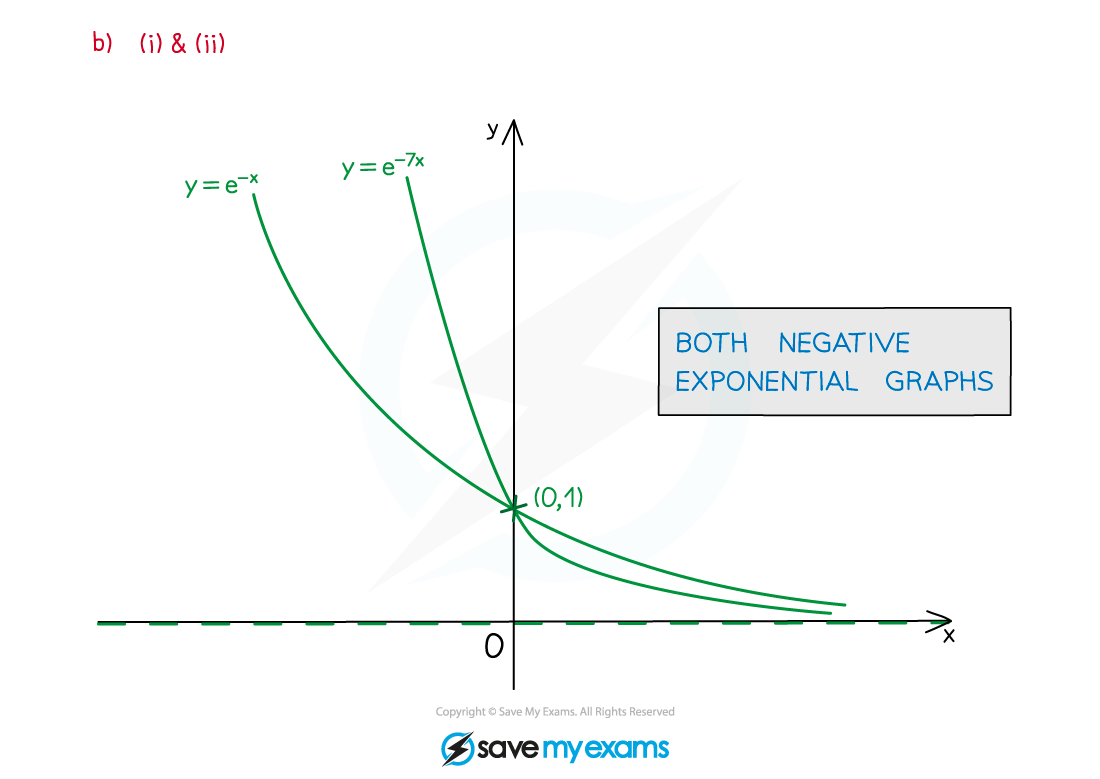
The negative exponential graph

• y = e^-x is a reflection in the y-axis of y = e^x
  

  

 

What is exponential growth and decay?

 

• y = Ae^kx (k > 0) is exponential growth
• y = Ae^-kx (k > 0) is exponential decay
• A is the initial value
• k is a (usually positive) constant
• A negative sign is used in the equation making clear whether it is growth or decay