Language of Functions (Cambridge O Level Additional Maths)

Revision Note

Test yourself

Author

Paul

Last updated

8 March 2024

Did this video help you?

Introduction to Functions

What is a mapping?

A mapping takes an 'input' from one set of values to an 'output' in another

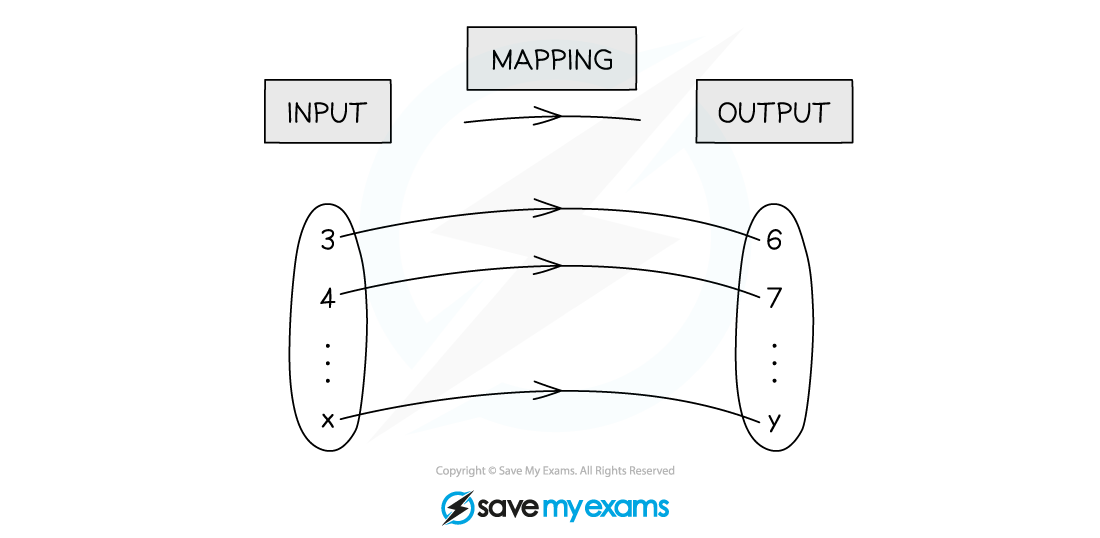
Input and output of a mapping

Mappings can be
- 'many-one' (many 'input' values map to one 'output' value)
- 'one-one' (one 'input' value maps to one 'output' value)
  - You may also come across 'many-many' and 'one-many' functions

What is a function?

A function is a mapping where every 'input' value maps to a single 'output'
Therefore only many-one and one-one mappings are functions

What notation is used for functions?

Functions are denoted by $f (x), g (x)$ , etc
- e.g. $f (x) = x^{2} - 3 x + 2$
- These would be pronounced as 'f of x', 'g of x', etc
There is an alternative notation
- e.g. $f : x \mapsto x^{2} - 3 x + 2$
- Which may be pronounced 'the function f maps x to x-squared minus three x plus two'

How does a function work?

A function has an input $(x)$ and output $(f (x) or y)$
Whatever goes in the bracket (instead of $x$ ) with f, replaces the $x$ on the other side
- This is the input
If the input is known, the output can be calculated
- For example, given the function $f (x) = 2 x + 1$
  - $f (3) = 2 \times 3 + 1 = 7$
  - $f (- 4) = 2 \times (- 4) + 1 = - 7$
  - $f (a) = 2 a + 1$

If the output is known, an equation can be formed and solved to find the input
- For example, given the function $f (x) = 2 x + 1$
  - If $f (x) = 15$ , the equation $2 x + 1 = 15$ can be formed
  - Solving this equation gives an input of 7

Worked example

A function is defined as $f (x) = 3 x^{2} - 2 x + 1$ .

Find

f (7)

The input is

x = 7

, so substitute 7 into the expression everywhere you see an

x

f (7) = 3 {(7)}^{2} - 2 (7) + 1

Calculate.

\begin{array}{rcl} f (7) & = & 3 (49) - 14 + 1 \\ = & 147 - 14 + 1 \end{array}

f (7) = 134

Find

f (x + 3)

The input is

x = x + 3

so substitute

x + 3

into the expression everywhere you see an

x

$f (x + 3) = 3 {(x + 3)}^{2} - 2 (x + 3) + 1$

Expand the brackets and simplify.

$\begin{array}{rcl} f (x + 3) & = & 3 (x^{2} + 6 x + 9) - 2 (x + 3) + 1 \\ = & 3 x^{2} + 18 x + 27 - 2 x - 6 + 1 \\ = & 3 x^{2} + 16 x + 22 \end{array}$

$f (x + 3) = 3 x^{2} + 16 x + 22$

A second function is defined $g : x \mapsto 3 x - 4$ .

Find the value of

x

for which

g : x \mapsto - 16

Form an equation by setting the function equal to -16.

\begin{array}{rcl} 3 x - 4 & = & - 16 \end{array}

Solve the equation by first adding 4 to both sides, then dividing by 3.

\begin{array}{rcl} 3 x - 4 & = & - 16 \\ 3 x & = & - 12 \\ x & = & - \frac{12}{3} \end{array}

x = - 4

Domain & Range

What is the domain of a function?

The domain of a function is the set of values that are allowed to be the ‘input’
A function is only fully defined once its domain has been stated
- If a domain is not stated then it is assumed that the domain is the largest set of possible values
  - e.g. the largest set of possible values for the function $f (x) = \sqrt{x}$ would be $x \geq 0$
Restrictions on a domain can turn many-one functions into one-one functions

Restricting the domain can turn a many-one function into a one-one function

What is the range of a function?

The range of a function is the set of values of all possible ‘outputs’
The type of values in the range depend on the domain

How do I find a range from a given domain?

The domain of a function is the set of values that are used as inputs
The range of a function is the set of values that are given as outputs
Finding the range of a function involves determining all possible output values from a given domain
- This may need to be done by calculating each output value individually by applying the function to each input value
- Or by considering the shape or pattern of the function
To graph a function we use the inputs as the x-coordinates and the outputs as the y-coordinates
- $f (2) = 5$ corresponds to the coordinates (2, 5)
Graphing the function can help you visualise the range
- For example the range of the function $f (x) = x^{2}$ for a domain of all real values of $x$ will be $f (x) \geq 0$ as the y-coordinates on the graph are all greater than or equal to zero

Worked example

The many-one function, $f (x)$ , is given by

$f (x) = {(x - 3)}^{2}$

for all values of $x$ .

State the range of

f (x)

The 'output' from the function

f

is a squared value and so will be positive, or zero.

f \geq 0

The domain of

f (x)

is changed to

x > 5

.
Write down the changed range of

f (x)

x > 5

f (x) > {(5 - 3)}^{2}

∴ f > 4

The Modulus Function

What is the modulus function?

The modulus function makes any 'input' positive
- This is sometimes called the absolute value (of the input)
- The modulus function is indicated by a pair of vertical lines being written around the input
  - Similar to how brackets are used
  - e.g. $| 7 | = 7, | - 7 | = 7$

What is the relationship between a function and its modulus?

For an 'output' such that $f (x) \geq 0$ , then $| f (x) | = f (x)$
- Both the function and its modulus are positive

For an 'output' such that $f (x) < 0$ , then $| f (x) | = - f (x)$
- The function value is negative, but its modulus is positive

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves: