O LevelAdditional MathsCambridgeRevision NotesAlgebra & FunctionsFunctionsInverse Functions

Inverse Functions (Cambridge O Level Additional Maths)

Revision Note

Test yourself
Paul

Author

Paul

Last updated

Inverse Functions

What is an inverse function?

  • An inverse function does the exact opposite of the function it came from
    • For example, if the function “doubles the number and adds 1” then its inverse is
    • “subtract 1 and halve the result”
  • It is the inverse operations in the reverse order

How do I write inverse functions?

  • An inverse function f-1 can be written as space straight f to the power of negative 1 end exponent left parenthesis x right parenthesis space equals space horizontal ellipsis space space or  straight f to the power of negative 1 end exponent space colon space x space rightwards arrow from bar space horizontal ellipsis
    • For example, if straight f left parenthesis x right parenthesis space equals space 2 x space plus space 1 its inverse can be written as
    • straight f to the power of negative 1 end exponent left parenthesis x right parenthesis space equals space fraction numerator left parenthesis x space – space 1 right parenthesis space over denominator 2 end fraction  or   straight f to the power of negative 1 end exponent colon space x space rightwards arrow from bar space fraction numerator left parenthesis x space – space 1 right parenthesis over denominator 2 end fraction

How do I find an inverse function?

  • The easiest way to find an inverse function is to 'cheat' and swap the x and y variables
    • Note that this is a useful method but you MUST remember not to do this in any other circumstances in maths
  • STEP 1
    Write the function in the formspace y space equals space horizontal ellipsis
    e.g.       y space equals space 2 x space plus space 1
  • STEP 2
    Swap the x's andspace y's to get x space equals space horizontal ellipsis
    e.g.      x space equals space 2 y space plus space 1
  • STEP 3
    Rearrange the expression to make y the subject again
    table row cell x space minus space 1 space end cell equals cell space 2 y end cell row cell fraction numerator x space minus space 1 over denominator 2 end fraction space end cell equals cell space y space space space space space space rightwards arrow space space space y space equals space fraction numerator x space minus space 1 over denominator 2 end fraction end cell end table
  • STEP 4
    Rewrite using the correct notation for an inverse function
    • either as f-1(x) = … or f-1 : x ↦ …
    • yshould not exist in the final answer
      • e.g.  straight f to the power of negative 1 end exponent open parentheses x close parentheses space equals space fraction numerator space x italic space minus space 1 over denominator 2 end fraction

How does a function relate to its inverse?

  • If straight f open parentheses 3 close parentheses equals 10 then the input of 3 gives an output of 10
    • The inverse function undoes f(x)
    • An input of 10 into the inverse function gives an output of 3
      • If straight f open parentheses 3 close parentheses equals 10 then straight f to the power of negative 1 end exponent open parentheses 10 close parentheses equals 3
  • ff to the power of negative 1 end exponent open parentheses x close parentheses equals straight f to the power of negative 1 end exponent straight f open parentheses x close parentheses equals x
    • If you apply a function to x, then immediately apply its inverse function, you get x
      • Whatever happened to x gets undone
    • f and f-1 cancel each other out when applied together
  • If straight f open parentheses x close parentheses space equals space 2 to the power of x and you want to solve straight f to the power of negative 1 end exponent open parentheses x close parentheses space equals space 5
    • Finding the inverse function straight f to the power of negative 1 end exponent open parentheses x close parentheses in this case is tricky (impossible if you haven't studied logarithms)
    • instead, take f of both sides and use that ff to the power of negative 1 end exponent cancel each other out:

table row cell ff to the power of negative 1 end exponent open parentheses x close parentheses end cell equals cell straight f open parentheses 5 close parentheses end cell row x equals cell straight f open parentheses 5 close parentheses end cell row x equals cell 2 to the power of 5 equals 32 end cell end table

Worked example

Find the inverse of the function straight f open parentheses x close parentheses space equals space 5 space minus space 3 x.

Write the function in the form y space equals space 5 space minus space 3 x and then swap the x and y.
 

y space equals space 5 space minus space 3 x x space equals space 5 space minus space 3 y

Rearrange the expression to make y the subject again.

table row cell x space end cell equals cell space 5 space minus space 3 y end cell row cell space x space plus space 3 y space end cell equals cell space 5 end cell row cell 3 y space end cell equals cell space 5 space minus space x end cell row cell y space end cell equals cell space fraction numerator 5 space minus space x over denominator 3 end fraction end cell end table

 
Rewrite using the correct notation for an inverse function.

Domain & Range of Inverse Functions

How do I find the domain and range of inverse functions?

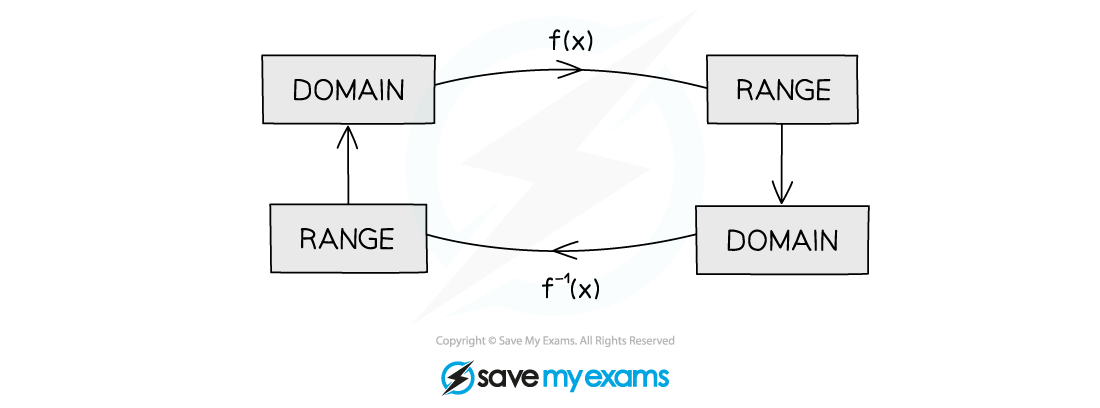
Domain and range of a function swap for its inverse

 

  • The range of a function will be the domain of its inverse function
  • The domain of a function will be the range of its inverse function

Worked example

A function is defined as straight f stretchy left parenthesis x stretchy right parenthesis equals square root of 3 x minus 2 end root comma space space x greater than fraction numerator 3 over denominator 2 space end fraction.

Write down the domain and range of straight f to the power of negative 1 end exponent stretchy left parenthesis x stretchy right parenthesis.

The domain of an inverse function is the range of the function.

The range of straight f open parentheses x close parentheses is

straight f greater than 0

therefore The domain of  is bold italic x bold greater than bold 0

The range of an inverse function is the domain of the function.

therefore The range of is bold f to the power of bold minus bold 1 end exponent bold greater than bold 3 over bold 2

Graphs of Inverse Functions

How are the graphs of a function and its inverse related?

  • The graph of an inverse function, y equals straight f to the power of negative 1 end exponent open parentheses x close parentheses, is a reflection of the graph of the function, y equals straight f open parentheses x close parentheses, in the line y equals x
  • Key features of the graph of y equals straight f open parentheses x close parentheses will be reflected, such as
    • x and y axes intercepts
    • turning points
    • asymptotes

How do I sketch the graph of an inverse function?

  • STEP 1
    • Sketch the line y equals x, and if need be, the graph of y equals straight f open parentheses x close parentheses
  • STEP 2
    • Reflect the graph of y equals straight f open parentheses x close parentheses in the line y equals x
      • Remember it is a sketch, but the graphs together should look like reflections
    • Consider points where the reflected graph will intersect the x and y axes
      • e.g.  The point open parentheses 4 comma space 0 close parentheses will be reflected to the point open parentheses 0 comma space 4 close parentheses
    • Consider any asymptotes on the graph of y equals straight f open parentheses x close parentheses - these will also be need reflecting
      • e.g.  The asymptote (line) x equals negative 2 will be reflected to the line y equals negative 2
    • Consider any restrictions on the domain and range of straight f open parentheses x close parentheses
      • e.g.  If the domain is x greater than 0 only sketch the graph for positive values of x
  • STEP 3
    • Label key points on the sketch of y equals straight f to the power of negative 1 end exponent open parentheses x close parentheses and state the equations of any asymptotes
  • This process works the other way round - the graph of y equals straight f open parentheses x close parentheses can be sketched from the graph of y equals straight f to the power of negative 1 end exponent open parentheses x close parentheses

Examiner Tip

  • If not given, sketch the graphs of y equals straight f open parentheses x close parentheses and y equals x to help sketch the graph of the inverse, y equals straight f to the power of negative 1 end exponent open parentheses x close parentheses
  • If the graph of y equals straight f open parentheses x close parentheses is given you do not need to know the expression for straight f open parentheses x close parentheses to sketch y equals straight f to the power of negative 1 end exponent open parentheses x close parentheses
    • Just reflect whatever is given in the line y equals x

Worked example

The diagram below shows the graph of y equals straight f open parentheses x close parentheses, where straight f open parentheses x close parentheses equals 4 minus 4 over x comma space space x greater than 0.

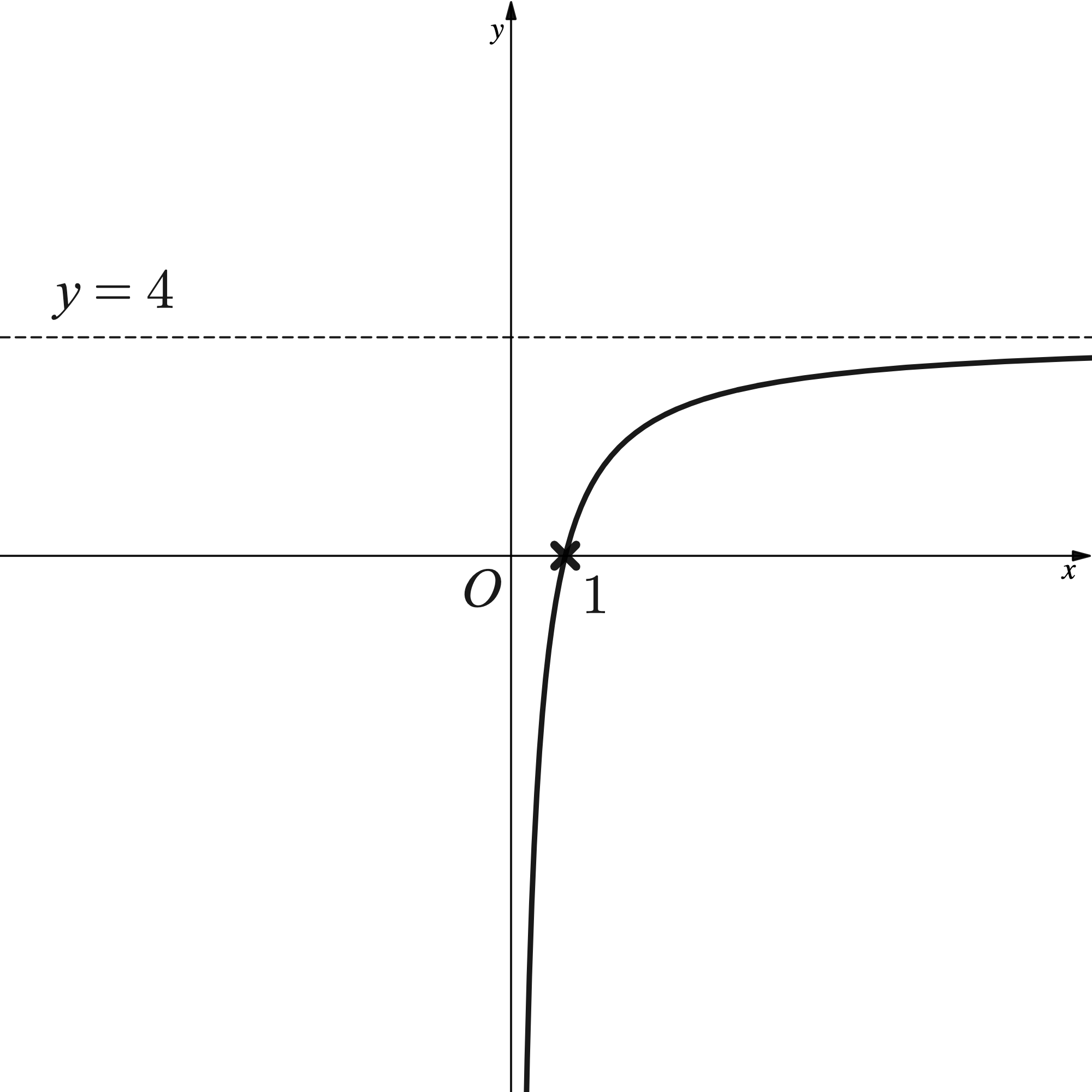
desmos-graph-6

a)
On a copy of the diagram, sketch the graph of y equals straight f to the power of negative 1 end exponent open parentheses x close parentheses.
Label the point where the graph crosses the y-axis and write down the equation of the asymptote.

The graph of an inverse function is the reflection of the graph of that function in the line y equals x.
Draw the line y equals x to help sketch the inverse function.
The x-axis intercept open parentheses 1 comma space 0 close parentheses becomes the y-axis intercept, open parentheses 0 comma space 1 close parentheses.
The (horizontal) asymptote y equals 4 will. become the (vertical) asymptote x equals 4.

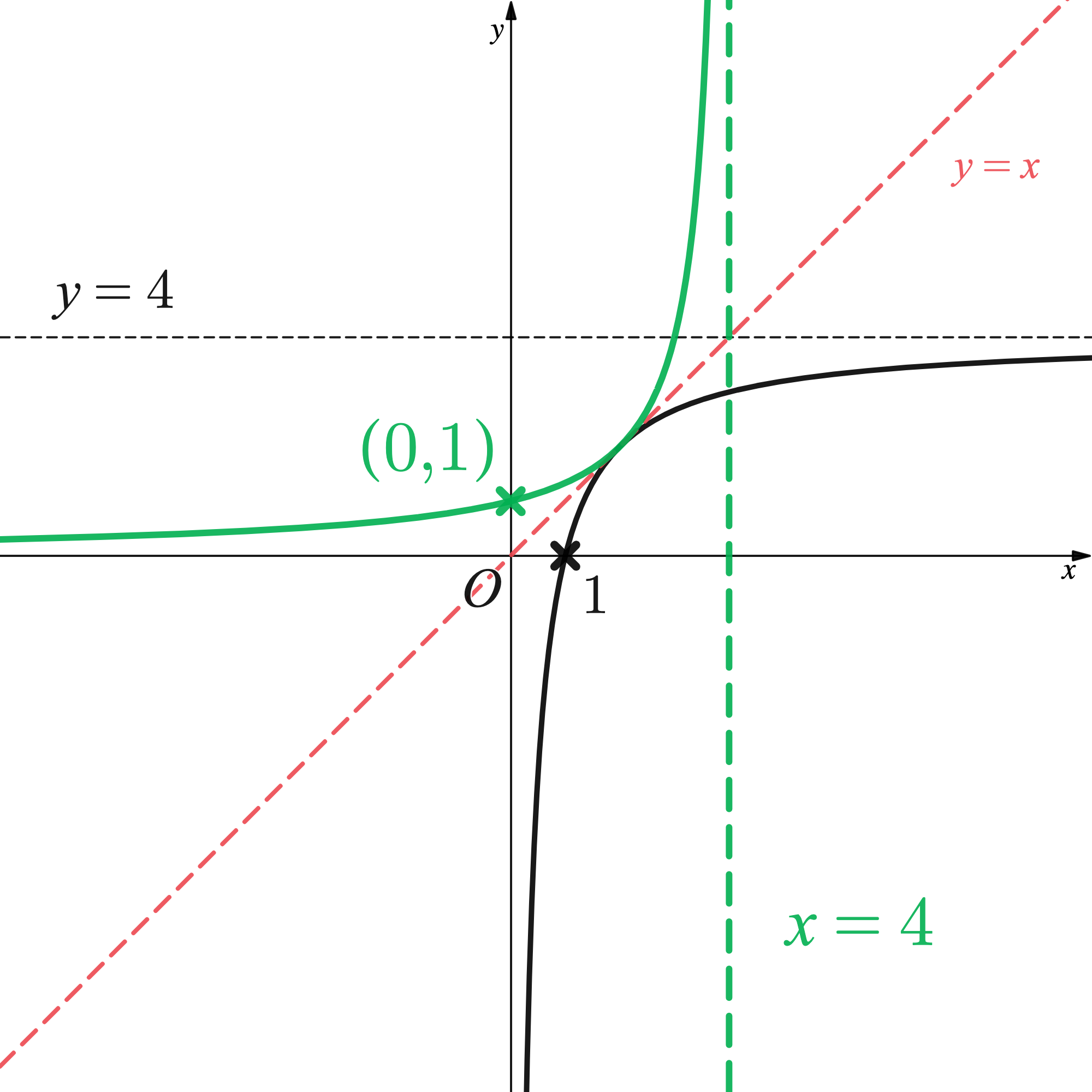
desmos-graph-5

b)
Use your sketch, or otherwise, to write down the value of x such that straight f open parentheses x close parentheses equals straight f to the power of negative 1 space end exponent open parentheses x close parentheses.

This will be the point at which the two graphs meet.
The point will be on the line y equals x so there is no need to work out straight f to the power of negative 1 end exponent open parentheses x close parentheses.
By sketching the graph in part (a) this point (with coordinates open parentheses 2 comma space 2 close parentheses) should have already been considered.
Only the x value is required.

bold italic x bold equals bold 2
The x value could also be found by solving straight f open parentheses x close parentheses equals x.

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfNext topic

    Did this page help you?

    Paul

    Author: Paul

    Expertise: Maths

    Paul has taught mathematics for 20 years and has been an examiner for Edexcel for over a decade. GCSE, A level, pure, mechanics, statistics, discrete – if it’s in a Maths exam, Paul will know about it. Paul is a passionate fan of clear and colourful notes with fascinating diagrams – one of the many reasons he is excited to be a member of the SME team.