Solving Cubic Equations

What is a cubic equation?

A cubic function is an polynomial of degree 3
- i.e. the highest power of $x$ is 3
A cubic equation can be written in the form
- $a x^{3} + b x^{2} + c x + d = 0$
Solving a cubic equation involves factorising the cubic function first.

How do I factorise a cubic function?

Factorising a cubic (function) combines the factor theorem with the method of polynomial division
The example below shows the steps for factorising a cubic

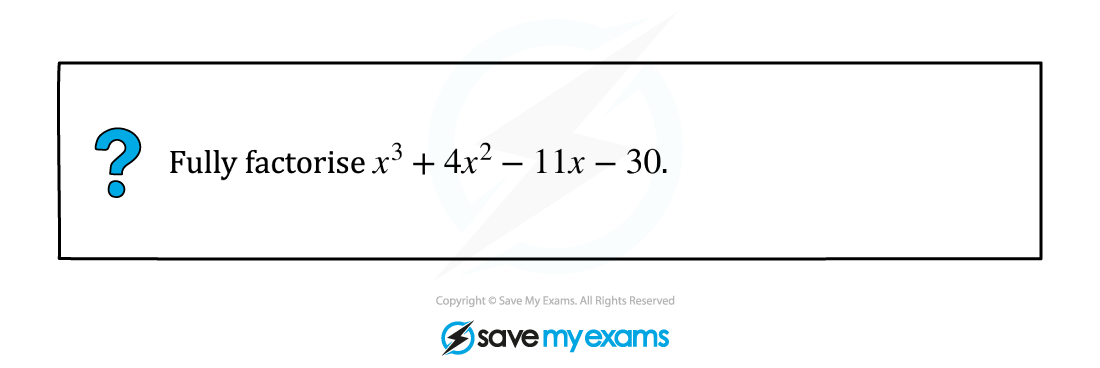
STEP 1
Use factor theorem.
Find a value $p$ such that $f (p) = 0$ .

factorising a cubic - step 1

STEP 2
Use polynomial division.
Divide $f (x)$ by $(x - p)$ .
(It is possible to do this step 'by inspection', see the worked example below)

STEP 3
Use the result of your division to write $f (x) = (x - p) (a x^{2} + b x + c)$ . factorising a cubic - step 3

STEP 4
If the quadratic $(a x^{2} + b x + c)$ can be factorised, do so.
$f (x)$ can then be written as the product of three linear factors.
If the quadratic cannot be factorised, then the result from STEP 3 is the final factorisation.

factorising a cubic - final answer

How do I solve a cubic equation?

A cubic equation will have either 1, 2 or 3 (real) solutions
- (The cubic function will have either 1, 2 or 3 (real) roots)
Once the cubic function is factorised using the four steps above, there is one more step to carry out

STEP 5
Find the solutions to the cubic equation by making each factor equal to zero

- For each linear factor, $(x - p)$
  - $x - p = 0$
  - so $x = p$ is a solution
  - This is the factor theorem!
- For a quadratic factor, $(a x^{2} + b x + c)$
  - $a x^{2} + b x + c = 0$
  - use either the quadratic formula or completing the square (as it won't factorise)
    - this will give two of the solutions to the cubic equation
  - if there are no solutions to the quadratic equation there are no solutions other than that from the linear factor

From the example above,
- $x^{3} + 4 x^{2} - 11 x - 30 = (x + 2) (x + 5) (x - 3)$
- so the solutions to the cubic equation $x^{3} + 4 x^{2} - 11 x - 30 = 0$ are
  - $x = - 2, x = - 5$ and $x = 3$
Cubic equations can have equal (repeated) solutions
- e.g. ${(x - 2)}^{2} (x + 1)$ has two (equal and real) roots, $x = 2$ (repeated) and $x = - 1$
- e.g. ${(2 x - 1)}^{3}$ has three (equal and real) roots, $x = \frac{1}{2}$

Examiner Tip

When $d = 0$ (i.e. there is no constant term) then $x$ is a factor of the cubic function, and so $x = 0$ is a solution
- This is a special case of factor theorem, where $f (0) = 0$
  - spotting the factor of $x$ means there is no need to test values
- Take out a factor of $x$ and a quadratic function will remain
- Deal with the quadratic in any of the usual ways

Worked example

Solve the cubic equation

x^{3} - 10 x^{2} + 12 x + 8 = 0

STEP 1 - use factor theorem with $f (x) = x^{3} - 10 x^{2} + 12 x + 8$

$f (1) = {(1)}^{3} - 10 {(1)}^{2} + 12 (1) + 8 = 11 \neq 0$

$f (- 1) = {(- 1)}^{3} - 10 {(- 1)}^{2} + 12 (- 1) + 8 = - 15 \neq 0$

$f (2) = {(2)}^{3} - 10 {(2)}^{2} + 12 (2) + 8 = 0$

$∴ (x - 2)$ is a factor of $f (x)$

STEP 2 - polynomial division ( $f (x) \div (x - 2)$ ) or 'by inspection'
By inspection ...

$f (x) = (x - 2) (a x^{2} + b x + c)$

('cubic' ÷ 'linear' = 'quadratic')

$a = 1$

(because the $x^{3}$ is generated only from $x \times a x^{2}$ )

$c = - 4$

(because the constant term is generated only from $- 2 \times c$ )

Equate coefficients of $x$ (or $x^{2}$ ) terms to find $b$ ,

$12 = c - 2 b$

$b = \frac{- 4 - 12}{2} = - 8$

STEP 3

$f (x) = (x - 2) (x^{2} - 8 x - 4)$

STEP 4 - the quadratic does not factorise

STEP 5 - Use the factors to find the solutions

$\begin{array}{rcl} x - 2 & = & 0, x = 2 \end{array}$

$x^{2} - 8 x - 4 = 0, x = \frac{8 \pm \sqrt{64 + 16}}{2}, x = 4 \pm 2 \sqrt{5}$

(using the quadratic formula)

The solutions to $x^{3} - 10 x^{2} + 12 x + 8 = 0$ are $x = 2, x = 4 + 2 \sqrt{5}$ and $x = 4 - 2 \sqrt{5}$ .

Solving Cubic Equations (Cambridge O Level Additional Maths)

Revision Note