Graphs of Cubic Polynomials (Cambridge O Level Additional Maths)

Revision Note

Test yourself

Author

Paul

Last updated

12 September 2023

Graphs of Cubic Polynomials

What is a cubic polynomial?

A cubic polynomial is a function of the form $a x^{3} + b x^{2} + c x + d$
- $a, b, c$ and $d$ are constants
- it is a polynomial of degree 3
  - so $b, c$ and/or $d$ could be zero
To sketch the graph of a cubic polynomial it will need to be in factorised form
- e.g. $(2 x - 1) (x + 2) (x - 3)$ is the factorised form of $2 x^{3} - 3 x^{2} - 11 x + 6$

What does the graph of a cubic polynomial look like?

In general the graph of a cubic polynomial will take one of the four forms
- All are smooth curves that take some practice to sketch!

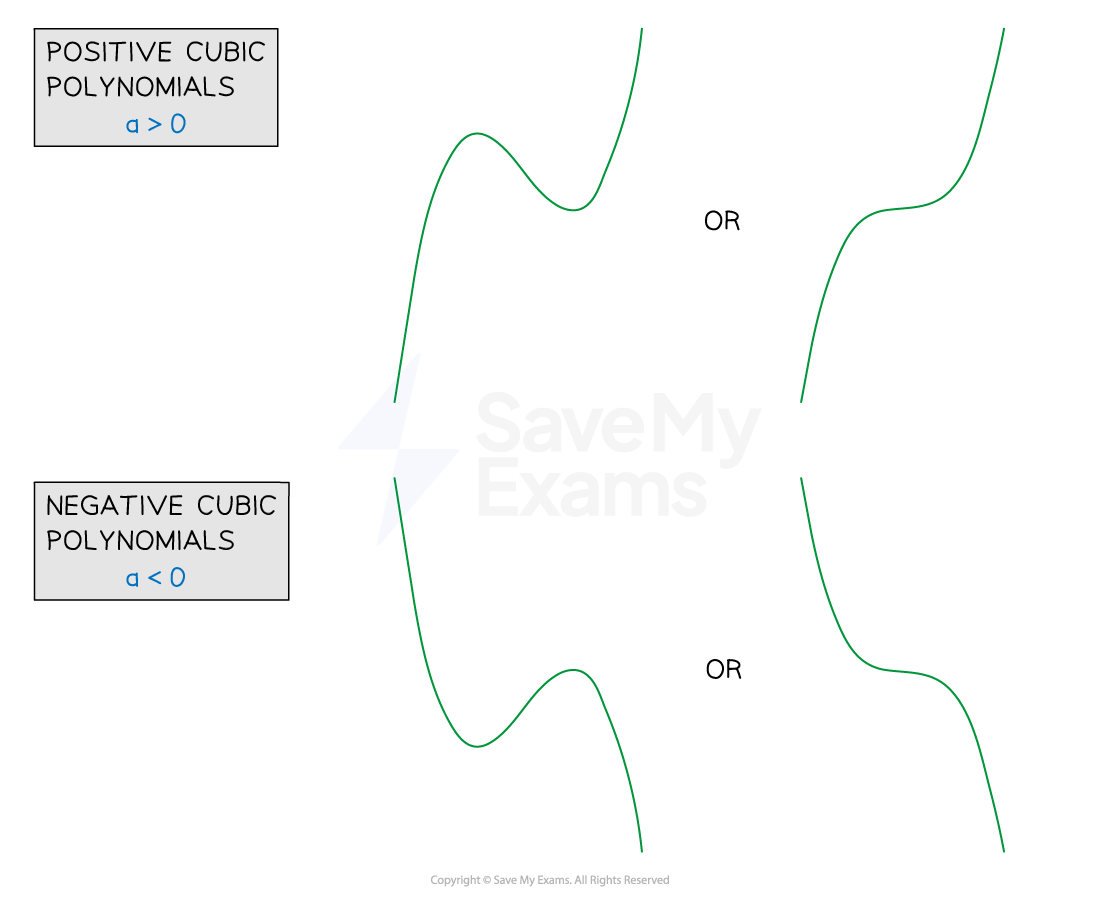
general shape of positive and negative cubic graphs

The exact form a particular cubic polynomial will depend on
- The number (and value) of roots ( $x$ -axis intercepts) of the cubic polynomial
- The $y$ -axis intercept
- The sign of the coefficient of the $x^{3}$ term ( $a$ )
  - If $a > 0$ the graph is a positive cubic ('starts' in the third quadrant, 'ends' in the first)
  - If $a < 0$ the graph is a negative cubic ('starts' in the second quadrant, 'ends' in the fourth)
- Turning points

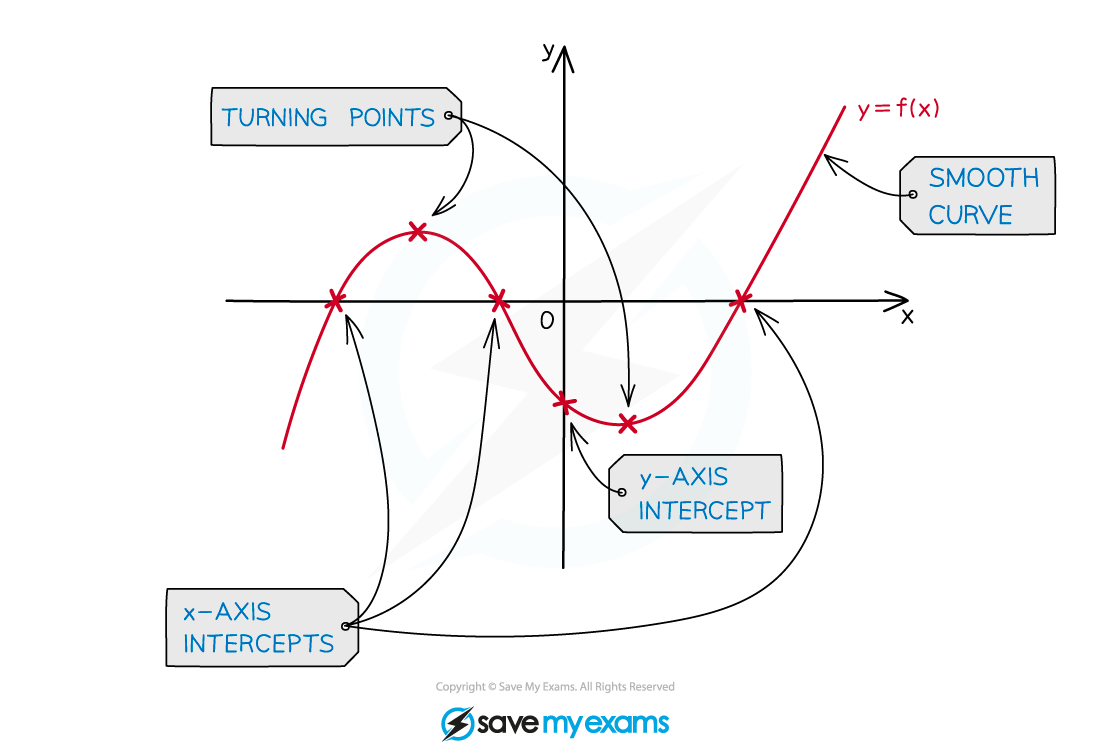
How do I sketch the graph of a cubic polynomial?

STEP 1
Find the $y$ -axis intercept by setting $x = 0$

STEP 2
Find the $x$ -axis intercepts (roots) by setting $y = 0$
(Any repeated roots will mean the graph touches - rather than crosses - the $x$ -axis)

STEP 3
Consider the shape of the graph - is it a positive cubic or a negative cubic?
Where does the graph 'start' and 'end'?

STEP 4
Consider where any turning points should go

STEP 5
Sketch the graph with a smooth curve, labelling points where the graph intercepts the $x$ and $y$ axes

Examiner Tip

In the exam, a cubic polynomial that requires sketching will be given in factorised form
- i.e. as the product of three linear factors
- a factor could be repeated
Build your sketch up as you work through each step to gradually build a mental picture of it
- If you need to redraw the graph for your final answer, that's fine!

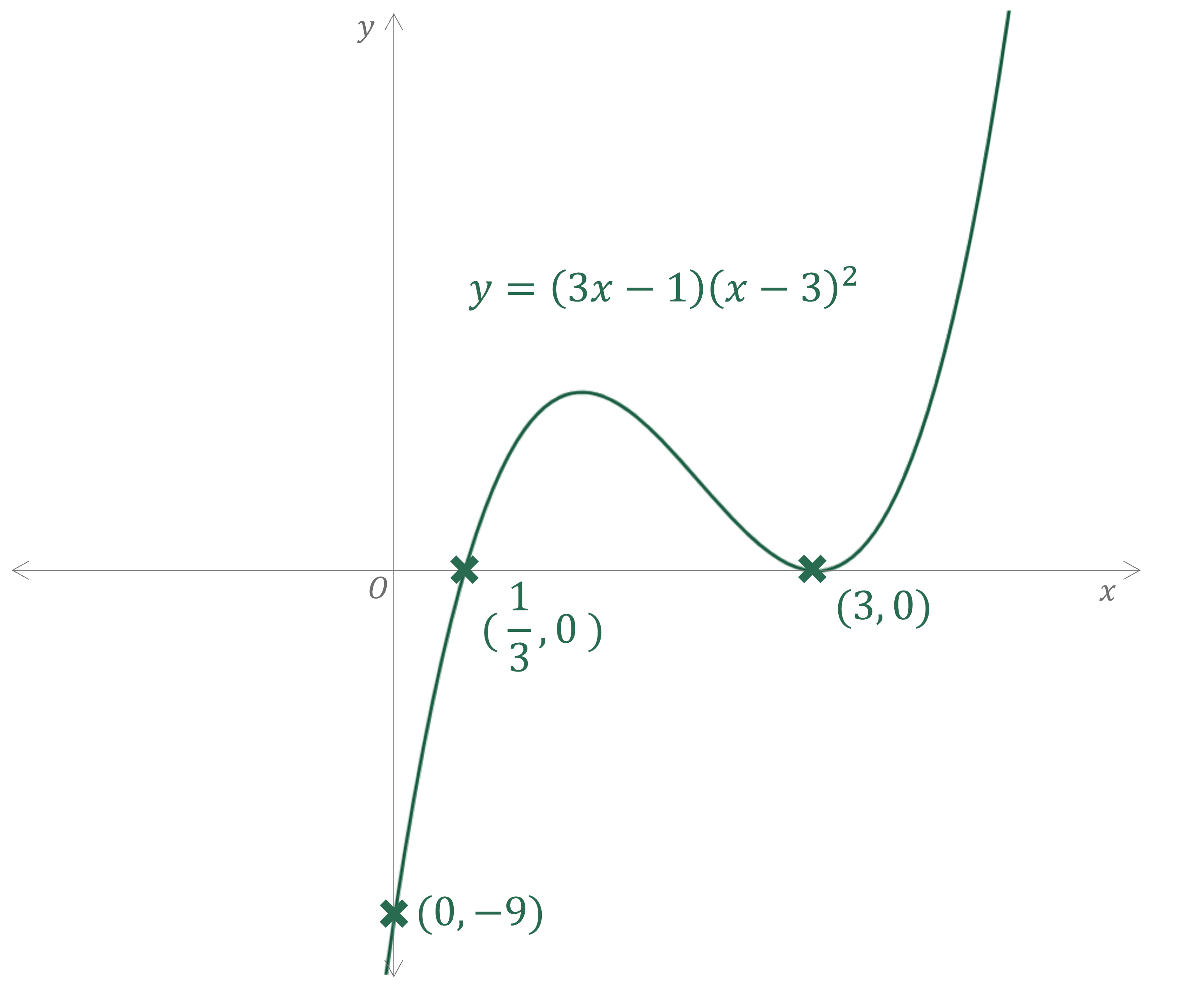
Worked example

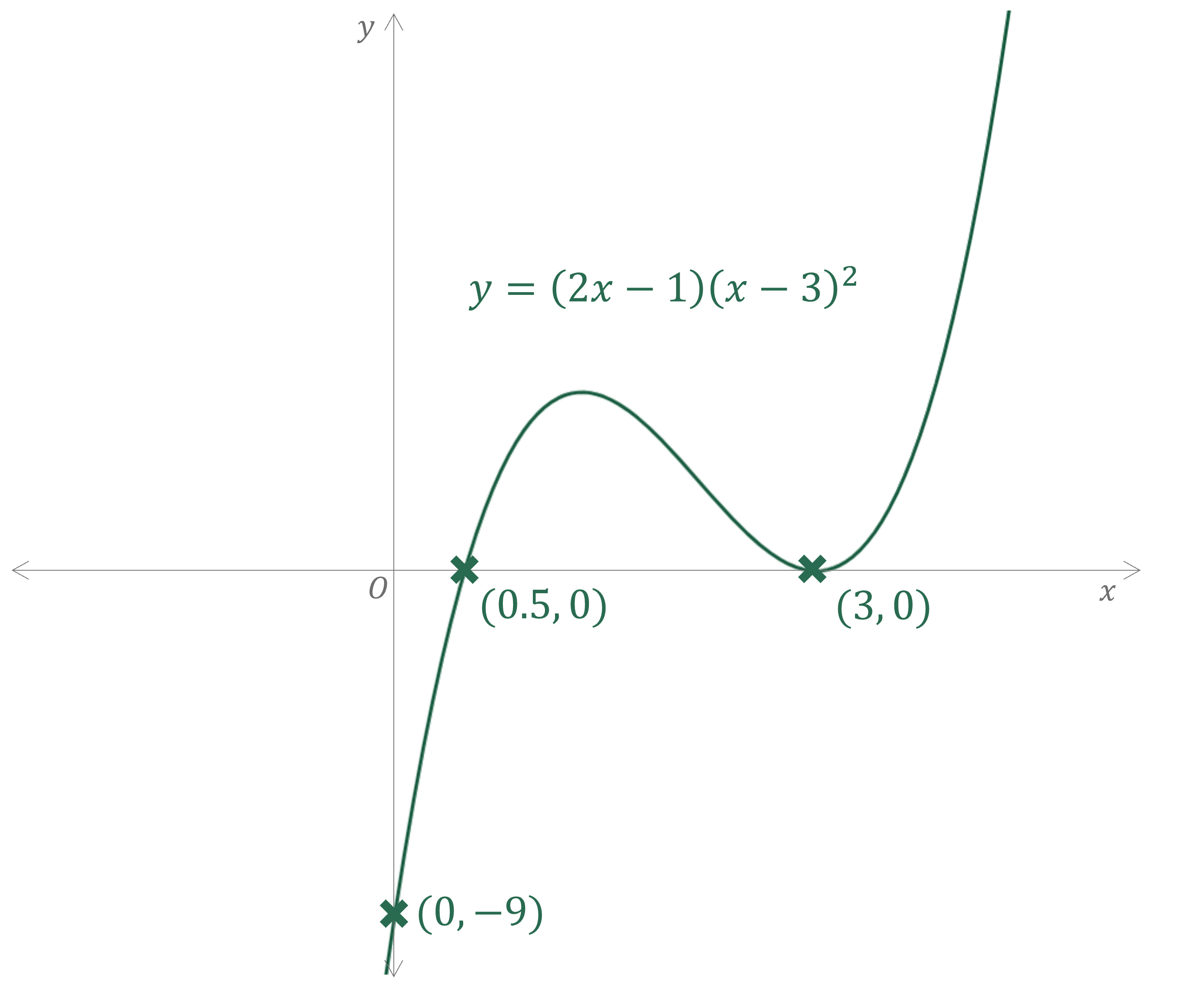
Sketch the graph of $y = (2 x - 1) {(x - 3)}^{2}$ .

STEP 1 - $y$ -axis intercept

$y = (- 1) {(- 3)}^{2} = - 9$

STEP 2 - $x$ -axis intercepts

$2 x - 1 = 0, x = \frac{1}{2}$

$x - 3 = 0, x = 3$ (repeated)

STEP 3 - shape, 'start'/'end'

$a > 0 (a = 2)$ so it is a positive cubic
$x = 3$ is a repeated root so the graph will touch the $x$ -axis at this point

STEP 4 - turning points

One turning point (minimum) will need to be where the curve touches the $x$ -axis
The other (maximum) will need to be between $x = \frac{1}{2}$ and $x = 3$

STEP 5 - smooth curve with labelled intercepts

worked example - final answer sketch of cubic showing intersections

Modulus Cubic Graphs

What is a modulus cubic graph?

A (factorised) cubic polynomial is of the from $f (x) = a (x - b) (x - c) (x - d)$
The graph of $y = f (x)$ must cross the $x$ -axis at least once
- therefore $y$ must take both positive and negative values
The modulus cubic graph, $y = | f (x) |$ will mean all values of $y$ are positive
- Any negative values become their positive equivalents
  - e.g. If $f (x) = x^{3}$ then $f (- 1) = {(- 1)}^{3} = - 1$ , but $| f (- 1) | = | {(- 1)}^{3} | = | - 1 | = 1$
A modulus cubic graph will not have any negative values
- the graph will not cross the $x$ -axis
- the graph will touch the $x$ -axis (at least once)

How do I sketch a modulus cubic graph?

Sketch the graph of the (original) cubic polynomial, $y = f (x)$
Any parts of this graph that are below the $x$ -axis should be reflected in the $x$ -axis to sketch the graph of $y = | f (x) |$

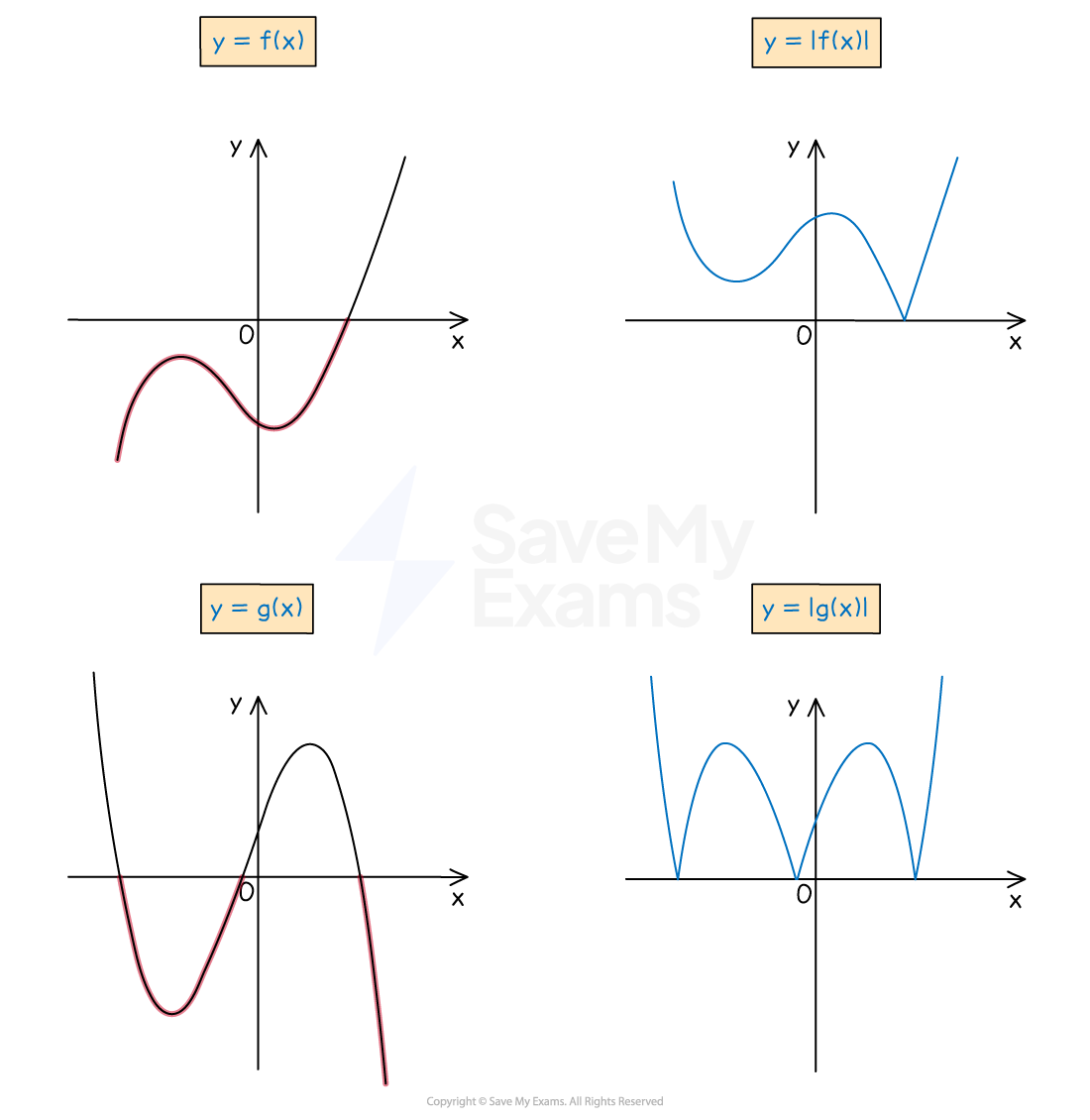
Cubic graphs and their modulus graphs

The points at which a modulus graph touches the $x$ -axis are the same as the points at which the original graph intercepts the $x$ -axis (i.e. the roots of $f (x)$ )
- Label these points, and the $y$ -axis intercept, on a sketch
Notice that the points at which a modulus graph touches the $x$ -axis are not smooth
- they are 'pointy' (V-shaped)
- turning points are smooth (U-shaped)

How do I find a cubic function from its modulus graph?

To deduce a cubic expression from its modulus graph consider
- whether the (original) expression could be a positive or negative cubic
  - a positive cubic 'starts' in the third quadrant and 'ends' in the first
  - a negative cubic 'starts' in the second quadrant and 'ends' in the fourth
    - a negative cubic can have a "-" at the start of its expression
- the $x$ -axis intercepts - the roots
  - for the roots $b, c$ and $d$ , write the factors $(x - b) (x - c) (x - d)$
- the $y$ -axis intercept - to deduce the expression in the form $a (x - b) (x - c) (x - d)$
  - lots of cubic functions have the same roots but have different coefficients
  - the $y$ -axis intercept should be the product $a \times - b \times - c \times - d = - a b c d$
    - $a$ may often, but not always, be 1

Examiner Tip

Sketching the (original) graph of $y = f (x)$ first is often helpful rather than trying to sketch the modulus graph from scratch
If asked to find a cubic function from a given graph
- there may be more than one possibility
  - consider which parts of the graph may have been reflected in the $x$ -axis
  - could it be either a positive or negative cubic polynomial?
- the factorised form is usually sufficient (unless a question says otherwise)

Worked example

The diagram below shows the graph of $y = | f (x) |$ where $f (x)$ is a positive cubic polynomial.

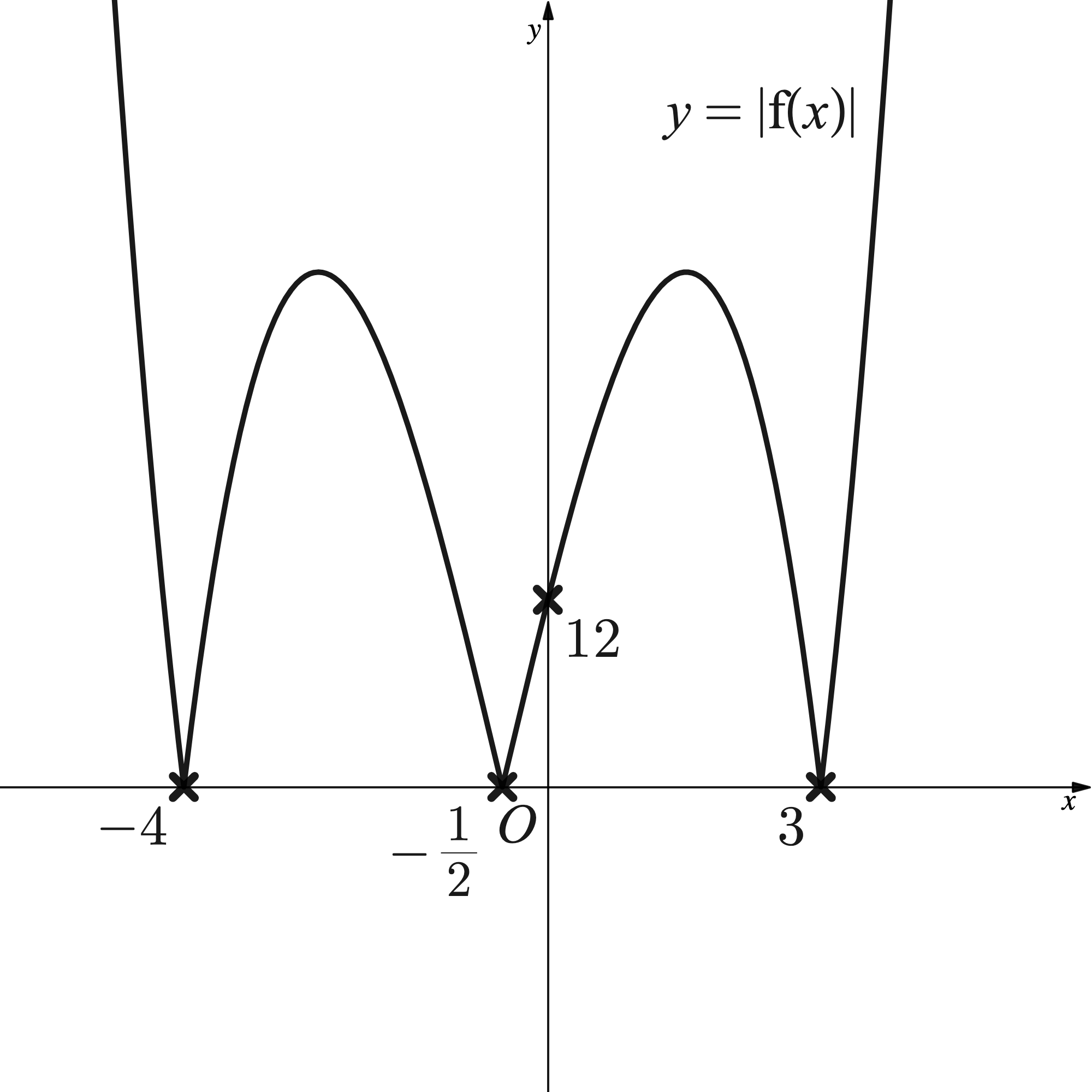
cie-adma25-2023-cubic-mod-1-we-question

Deduce an expression for $f (x)$ leaving your answer in factorised form, with each factor having integer coefficients.

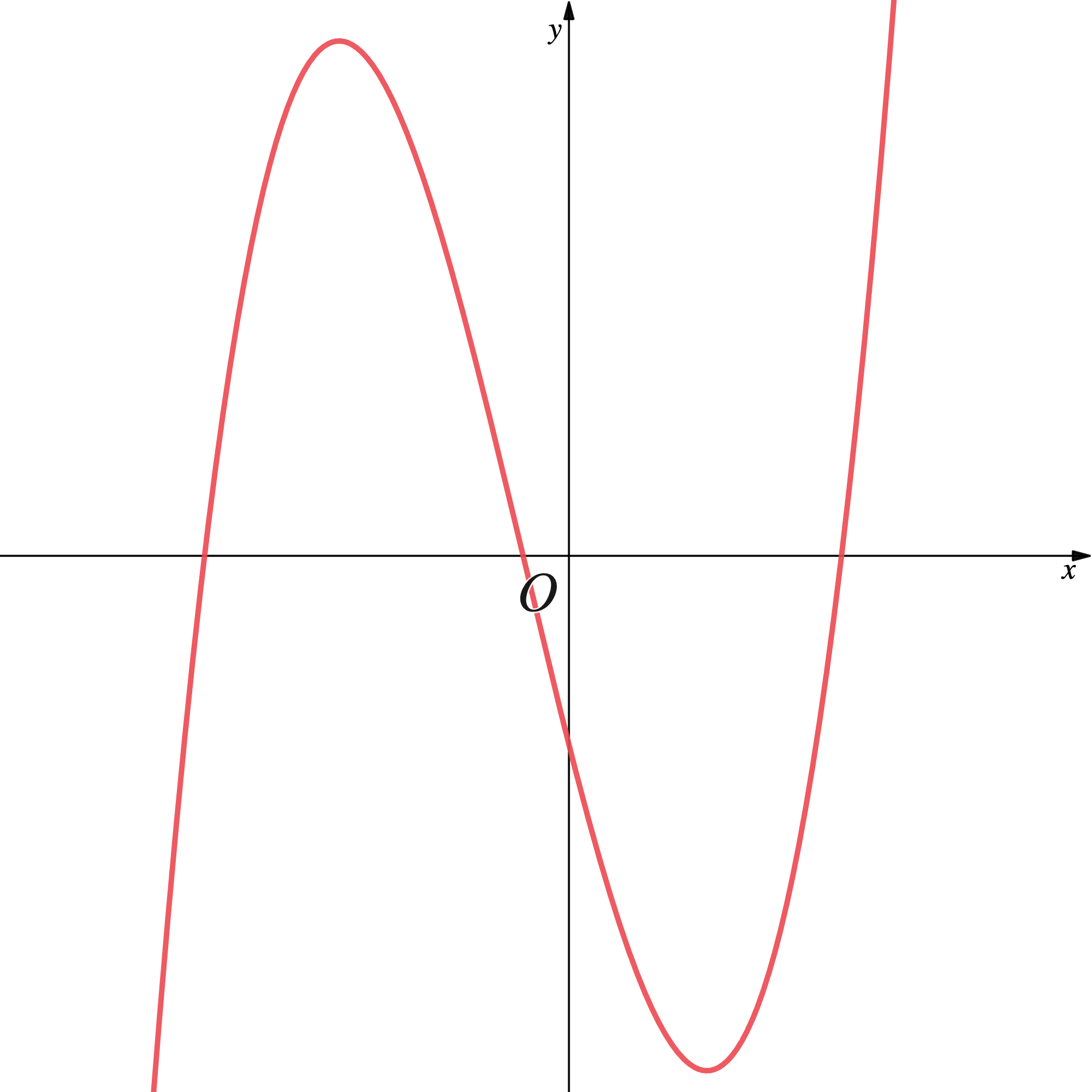
$f (x)$ is a positive cubic polynomial so the graph should 'start' in the third quadrant and 'end' in the first.
A quick sketch (without labels) can help.

cie-adma25-2023-cubic-mod-2-we-solution

The $x$ -axis intercepts indicate the roots.

$(x + 4) (x + \frac{1}{2}) (x - 3)$

The expression for $f (x)$ is of the form $a (x + 4) (x + \frac{1}{2}) (x - 3)$ .
Use the $y$ -axis intercept to deduce the value of $a$ .
From the sketch of $y = f (x)$ the $y$ -axis intercept is -12 (not 12).

$\begin{array}{rcl} a \times 4 \times \frac{1}{2} \times - 3 & = & - 12 \\ - 6 a & = & - 12 \\ a & = & 2 \end{array}$

The final answer requires each factor to have integer coefficients so multiply 2 into $(x + \frac{1}{2})$ and write down $f (x)$ .

$f (x) = (x + 4) (2 x + 1) (x - 3)$

Solving Cubic Inequalities Graphically

What is a cubic inequality?

A cubic function is of the form $f (x) = a x^{3} + b x^{2} + c x + d$ where $a, b, c$ and $d$ are constants
A cubic inequality can be any of the following
- $f (x) > 0$
- $f (x) \geq 0$
- $f (x) < 0$
- $f (x) \leq 0$
An inequality may need rearranging into one of these forms first before solving
- Furthermore, solving cubic equations graphically is easiest when the expression has been factorised
  - e.g. for a cubic with three (real) roots this would be $(x - p) (x - q) (x - r)$ where $p, q$ and $r$ are the roots

How do I solve a cubic inequality graphically?

STEP 1
If need be, rearrange the inequality so that one side of the inequality is zero
This should leave a cubic polynomial on the other side
Factorise the cubic polynomial if required
e.g. $(2 x - 3) (x - 4) (x + 1) \leq 0$

STEP 2
Sketch the graph of the cubic polynomial
The $x$ -axis intercepts (roots) are crucial to finding the solution but the $y$ -axis intercept is not needed
e.g.

sketch of a cubic using roots

STEP 3
Identify the part(s) of the graph that satisfy the inequality
Highlighting this on the sketch will help
Consider whether you need to include (≤, ≥) or exclude (<, >) the roots
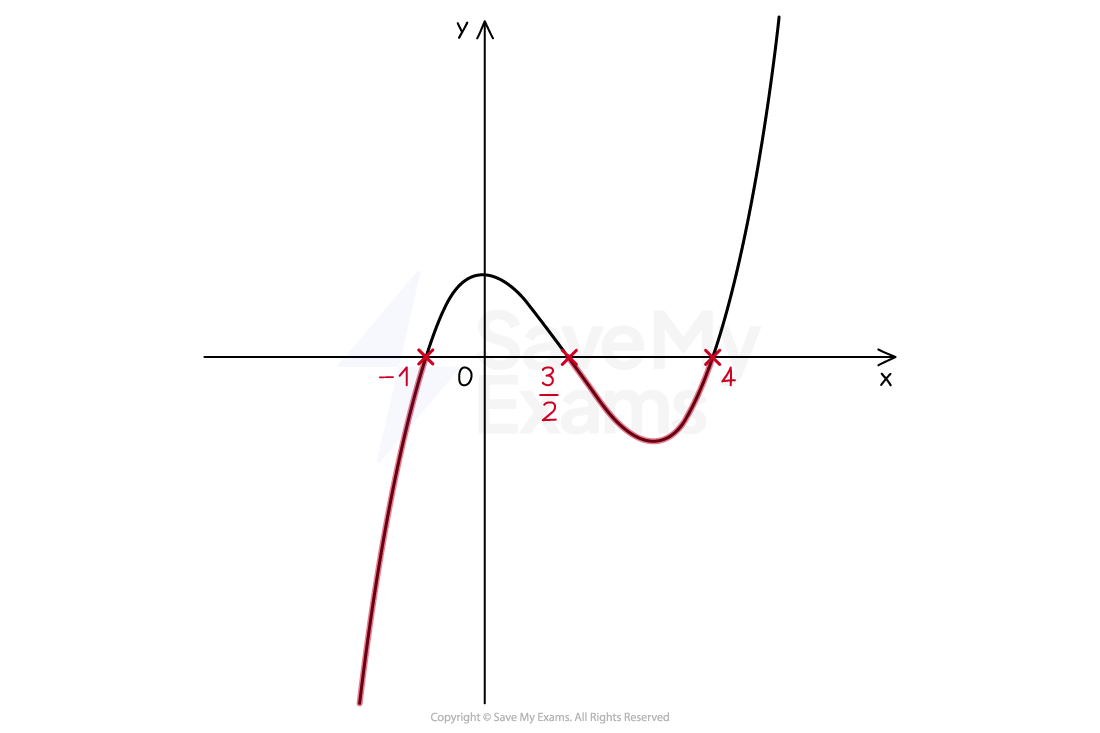
e.g. sketch of a cubic using roots, with highlighting of region less than zero

STEP 4
Write down the solutions to the inequality
e.g. $x \leq - 1, \frac{3}{2} \leq x \leq 4$

Worked example

Sketch the graph of

y = f (x)

where

f (x) = (3 x - 1) {(x - 3)}^{2}

This is a positive cubic polynomial with roots $x = \frac{1}{3}$ and $x = 3$

$x = 3$ is a repeated root so the graph will touch the $x$ -axis at this point

cie-adma25-2023-cubic-ineq-1-we-solution-dark-green

Hence solve the inequality

f (x) > 0

STEP 1 - the cubic polynomial is already in factorised form

STEP 2 - the graph has been sketched in part (a)

STEP 3 - Highlight the graph to show the parts of the graph which lie above zero

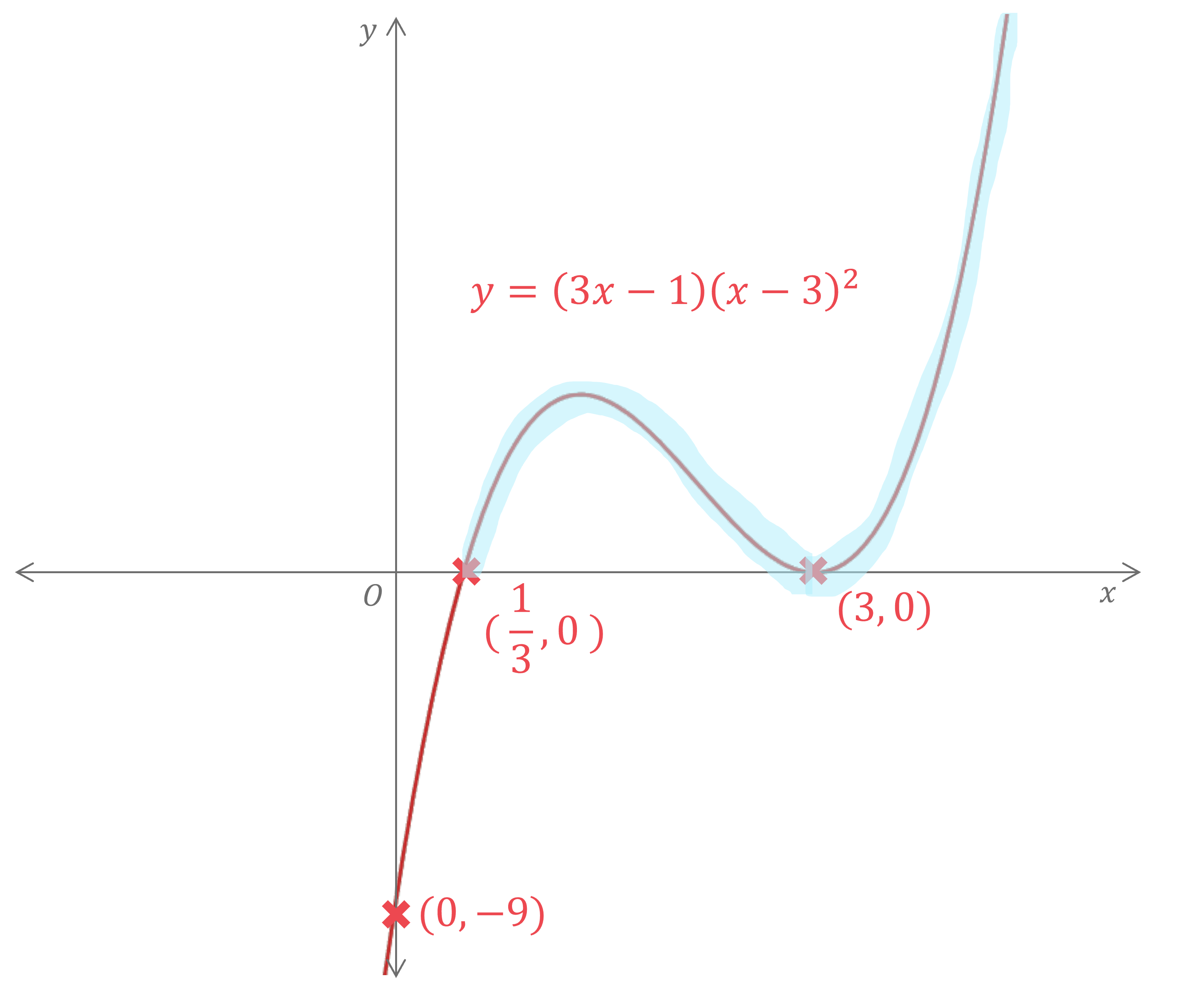
dQsDLIdG_cie-adma25-2023-cubic-ineq-2-we-solution-diff-colours

STEP 4 - Write the solution mathematically. Remember that in this case it is a strict inequality, so it cannot be equal to 3 or $\frac{1}{3}$

$x > \frac{1}{3}, x \neq 3$

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?

Graphs of Cubic Polynomials (Cambridge O Level Additional Maths)

Revision Note

What is a cubic polynomial?

What does the graph of a cubic polynomial look like?

How do I sketch the graph of a cubic polynomial?

What is a modulus cubic graph?

How do I sketch a modulus cubic graph?

How do I find a cubic function from its modulus graph?

What is a cubic inequality?

How do I solve a cubic inequality graphically?

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Paul