Level 3MathsAQAMathematical Studies (Core Maths)Paper 2C: Graphical TechniquesRevision NotesExponential FunctionsExponential FunctionsExponential Functions & Logarithms

Exponential Functions & Logarithms (AQA Level 3 Mathematical Studies (Core Maths))

Revision Note

Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

Exponential Functions & Logarithms

Before reading this section, make sure you have read Shapes of Exponential Graphs

  • A logarithm is the inverse of an exponential

  • If a space equals space b to the power of x then log subscript b a space equals space x

    • a space greater than space 0

    • b is called the base of the logarithm

  • When you read a logarithm statement, it can help to say to yourself:

    • "The power that you raise ... to, to get ... is ..."

      • log subscript 3 open parentheses 81 close parentheses equals 4 can be read as

      • “the power that you raise 3 to, to get 81, is 4”

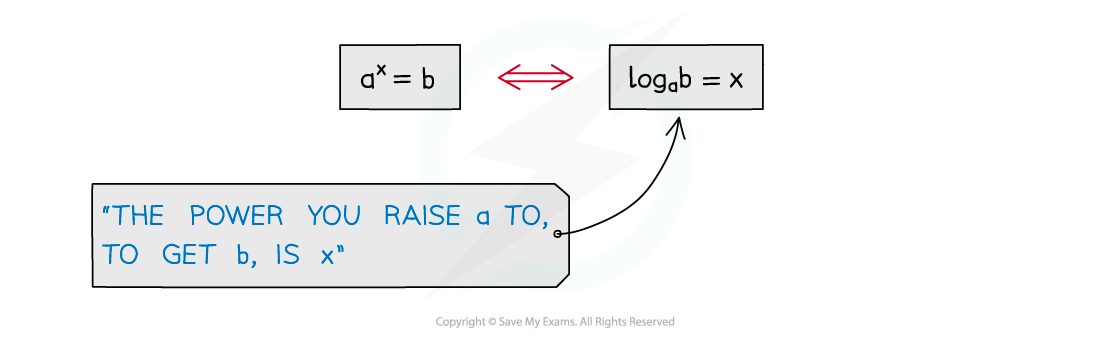
The power you raise a to, to get b, is x.

  • Here are some numerical examples:

    • 2 cubed equals 8 so log subscript 2 open parentheses 8 close parentheses equals 3

    • 5 squared equals 25 so log subscript 5 open parentheses 25 close parentheses equals 2

    • 10 to the power of 6 equals 1 space 000 space 000 so log subscript 10 open parentheses 1 space 000 space 000 close parentheses equals 6

    • 3 to the power of negative 2 end exponent equals 1 over 3 squared equals 1 over 9 so log subscript 3 open parentheses 1 over 9 close parentheses equals negative 2

How do I use logarithms to solve equations?

  • Use the relationship:

    • If a space equals space b to the power of x then log subscript b a space equals space x

    • To find any unknowns

  • For example

    • 3 to the power of x equals 2187 can be rewritten as a logarithm

      • log subscript 3 open parentheses 2187 close parentheses equals x

      • This can then be entered into your calculator

      • There should be a button which looks similar to box enclose log subscript box enclose blank end enclose end subscript open parentheses box enclose blank end enclose close parentheses end enclose

      • log subscript 3 open parentheses 2187 close parentheses equals 7 so x equals 7

Examiner Tips and Tricks

Remembering a simple numerical example such as:

2 cubed equals 8 so log subscript 2 open parentheses 8 close parentheses equals 3

can be a really useful reminder for how logarithms work.

Worked Example

A marketing company who work with an online video platform suggest that the number of views for a particular "viral" video can be modelled with the following equation:

V equals 1.56 to the power of t

where V is the number of views, and t is the time in hours since the video was published.

(a) Estimate the number of views, to the nearest 10, after 24 hours according to the model.

Substitute in t equals 24

V equals 1.56 to the power of 24 equals 43 space 150.9499...

Round to nearest 10

43 150 views

(b) Estimate the number of hours taken for the video to reach 1 million views according to the model. State your answer to the nearest hour.

Substitute in V equals 1 space 000 space 000

1 space 000 space 000 space equals space 1.56 to the power of t

Use the relationship:
If a space equals space b to the power of x then log subscript b a space equals space x
to rewrite as a logarithm

log subscript 1.56 end subscript open parentheses 1 space 000 space 000 close parentheses equals t

Type the logarithm into your calculator

t equals 31.06802578...

Round to nearest hour

31 hours

Last updated:

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Did this page help you?

    Previous:Velocity & AccelerationNext:The Number e
    Author
    Reviewer
    Jamie Wood

    Author: Jamie Wood

    Expertise: Maths

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.