Critical Activities & Critical Paths (AQA Level 3 Mathematical Studies (Core Maths))
Revision Note
Written by: Naomi C
Reviewed by: Dan Finlay
Critical Activities & Critical Paths
What is a critical activity?
In a project, some activities may be critical
Any delay to a critical activity will delay the entire project
Other activities in a project are not critical
There is some slack in the timing of a non-critical activity, it can be delayed without without delaying the entire project
Any slack time available is described by the float of an activity
float = latest finish time - earliest start time - duration of activity
If the float of an activity is equal to 0, it is a critical activity
If the float of an activity is greater than 0, it is not a critical activity
The float of an non-critical activity is the length of time it can be delayed for without delaying the entire project
What is a critical path?
A path through a network consisting only of critical activities is known as a critical path
Each activity on the critical path has a float of 0
The length of the critical path is the minimum duration of the entire project
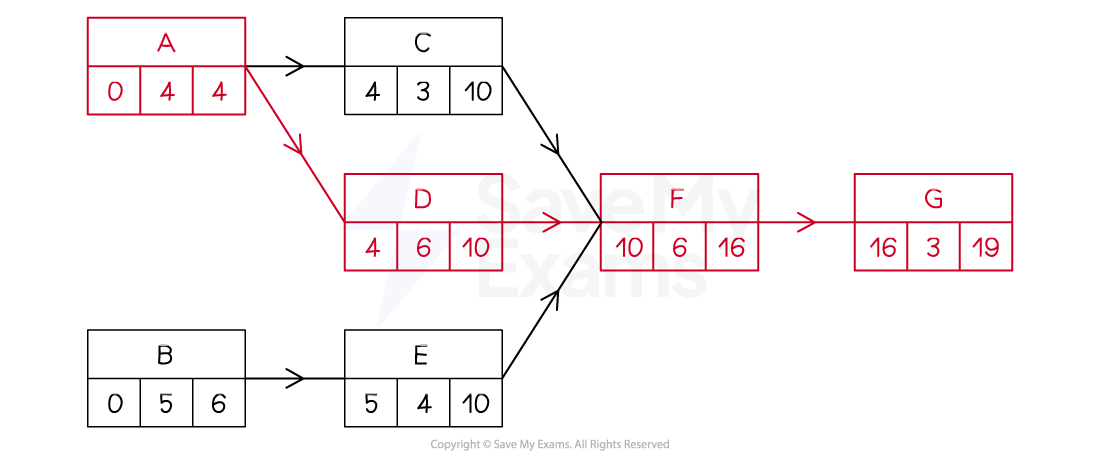
E.g. In the diagram below the critical path, A-D-F-G, is highlighted
Worked Example
An activity network is drawn for a new project and is shown below.
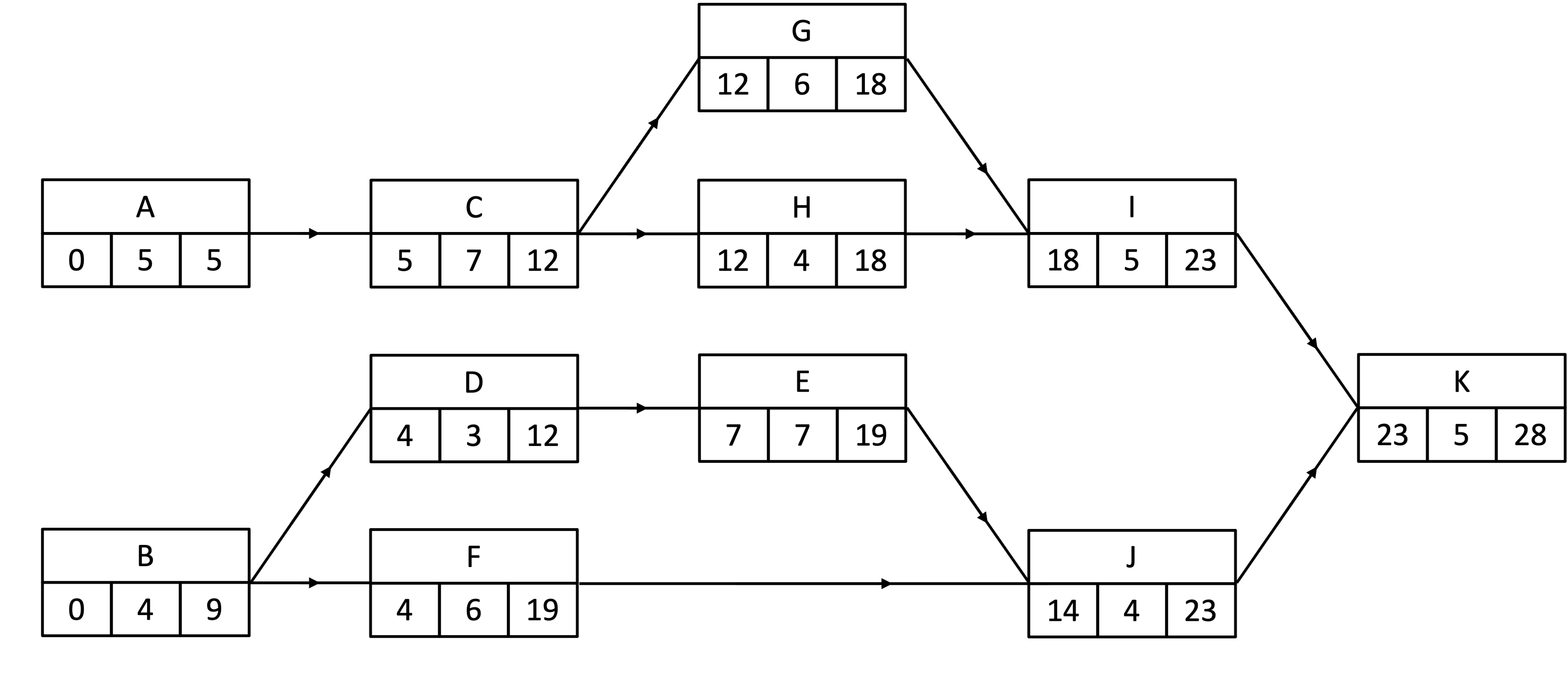
(a) Find the total float for activity F.
The float of an activity is found by subtracting the earliest start time and the duration of the activity from the latest finish time
Float = 19 - 6 - 4 = 9
Float of F: 9
(b) Identify the critical path.
Activities A, C, G, I and K all have no float so are critical activities
Critical path: A-C-G-I-K
(c) State the length of the minimum duration of the project.
The length of the minimum duration of the project is the length of the critical path
Minimum duration of the project: 28
Last updated:
You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
