The Normal Distribution (AQA Level 3 Mathematical Studies (Core Maths)): Revision Note
Exam code: 1350
Properties of the Normal Distribution
The normal distribution is an example of a continuous probability distribution
What is a continuous random variable?
A continuous random variable (often abbreviated to CRV) is a random variable that can take any value within a range of infinite values
Continuous random variables usually measure something
For example, height, weight, time, etc
What is a continuous probability distribution?
A continuous probability distribution is a probability distribution in which the random variable
is continuous
The probability of
being a particular value is always zero
for any value
Instead we define the probability density function
for a specific value
We talk about the probability of
being within a certain range
A continuous probability distribution can be represented by a continuous graph (the values for
along the horizontal axis and probability density on the vertical axis)
The area under the graph between the points
and
is equal to
The total area under the graph equals 1
As
for any value
, it does not matter if we use strict or weak inequalities
for any value
What is a normal distribution?
A normal distribution is a continuous probability distribution
The continuous random variable can follow a normal distribution if:
The distribution is symmetrical
The distribution is bell-shaped
If X follows a normal distribution then it is denoted
μ is the mean
σ2 is the variance
σ is the standard deviation
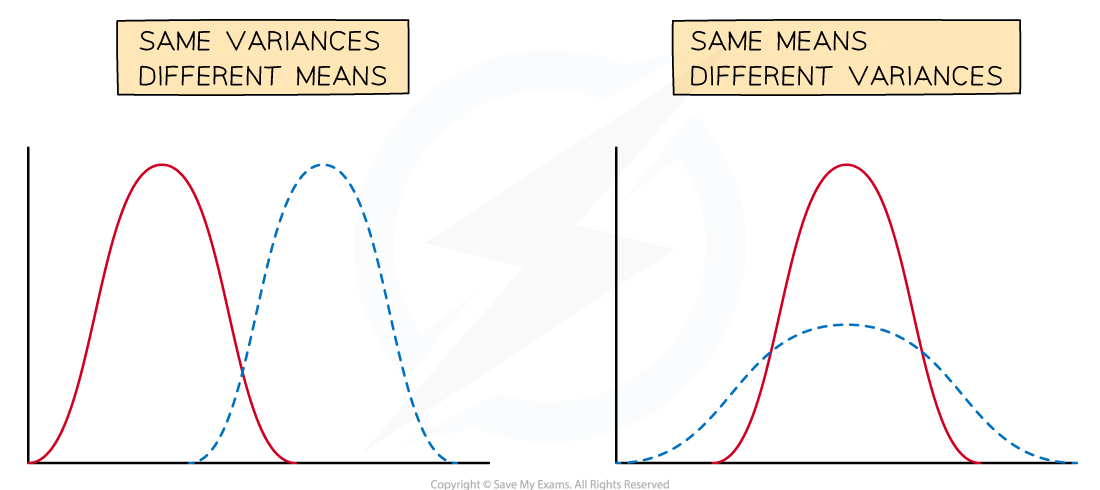
If the mean changes then the graph is translated horizontally
If the variance changes then the graph is stretched horizontally
A small variance leads to a tall curve with a narrow centre
A large variance leads to a short curve with a wide centre
What are the important properties of a normal distribution?
The mean is μ
The variance is σ2
If you need the standard deviation remember to square root this
The normal distribution is symmetrical about x = μ
Mean = Median = Mode = μ
The normal distribution curve has two points of inflection
x = μ ± σ (one standard deviation away from the mean)
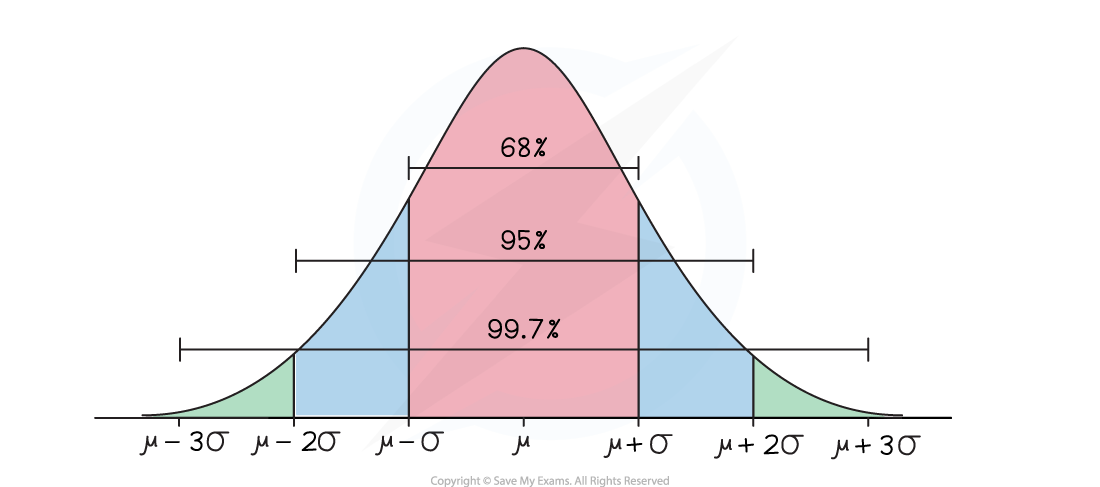
There are some useful approximate results:
Approximately two-thirds (68%) of the data lies within one standard deviation of the mean (μ ± σ)
Approximately 95% of the data lies within two standard deviations of the mean (μ ± 2σ)
Nearly all of the data (99.7%) lies within three standard deviations of the mean (μ ± 3σ)
Examiner Tips and Tricks
Even if an exam question doesn't explicitly ask you to sketch a diagram for a normally distributed function, it can often be really helpful!
Worked Example
For a certain species of cheetah, the speed at which they can run is normally distributed with a mean speed of 40 mph and a standard deviation of 9 mph.
(a) Write the distribution in notation form.
Answer:
Let S represent the continuous random variable speed
Calculate the variance by taking the square root of the standard deviation
92 = 81
Write the distribution in correct notation
S ~ N(40, 81)
(b) What percentage of the population of cheetahs would you expect to have a running speed between 22 mph and 58 mph?
Answer:
Sketching a diagram can help
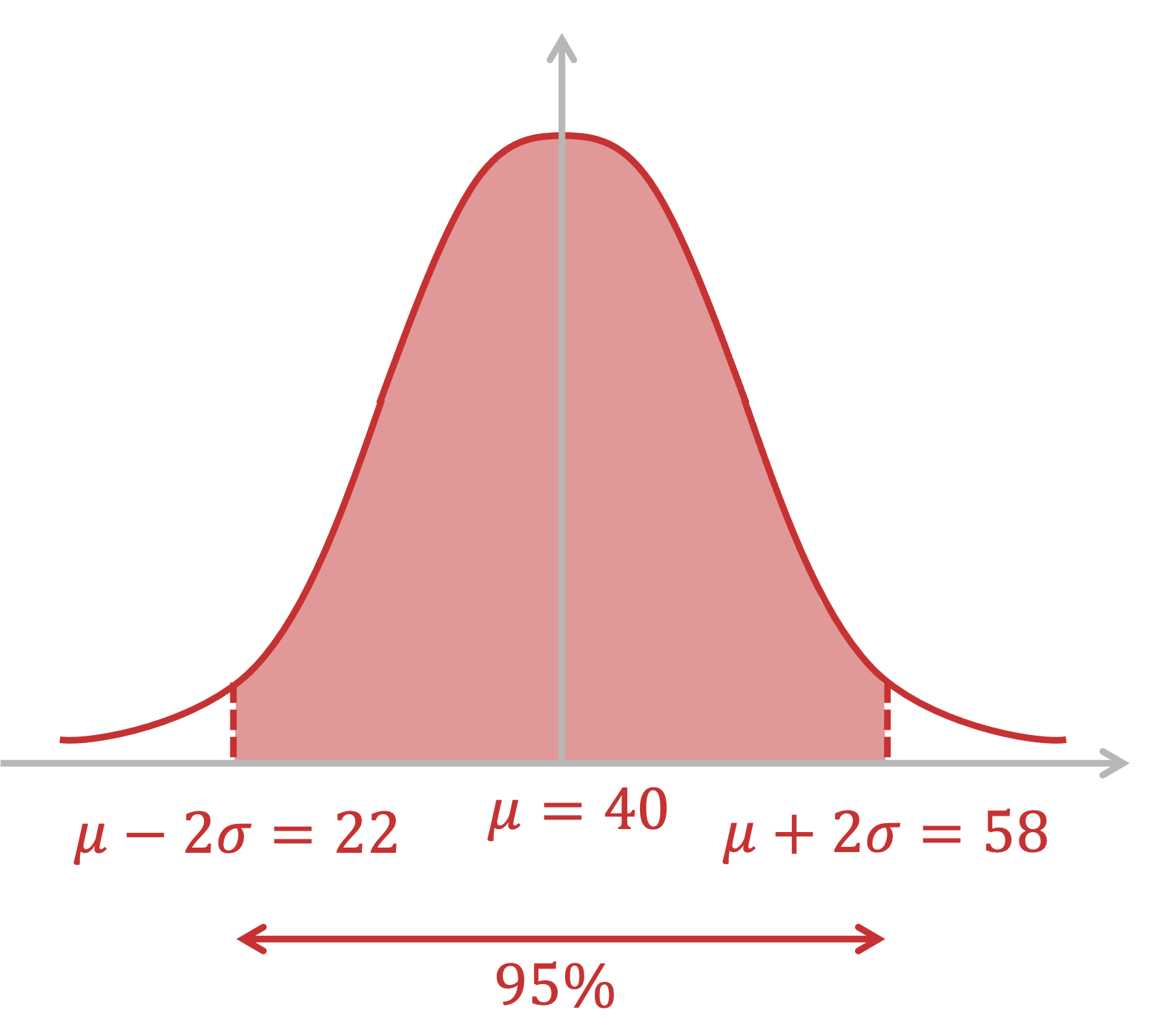
The values given in the question are two standard deviations above and below the mean
You should know that 95% of the results in a normal distribution will fall within this range
95%
Standard Normal Distribution
What is the standard normal distribution?
The standard normal distribution is a normal distribution where the mean is 0 and the standard deviation is 1
It is denoted by Z
The area under the curve is 1
Why is the standard normal distribution important?
Any normal distribution curve can be transformed to the standard normal distribution curve by a horizontal translation and a horizontal stretch
Therefore we have the relationship:
Where
and
So for any value x, a z-score (or z-value) can be calculated which measures how many standard deviations x is away from the mean
Finding the z-value is also known as standardising the variable
Probabilities are related by:
This will be useful when the mean or variance is unknown
If a value of x is less than the mean then the z-value will be negative
You can use the notation
which just means
Worked Example
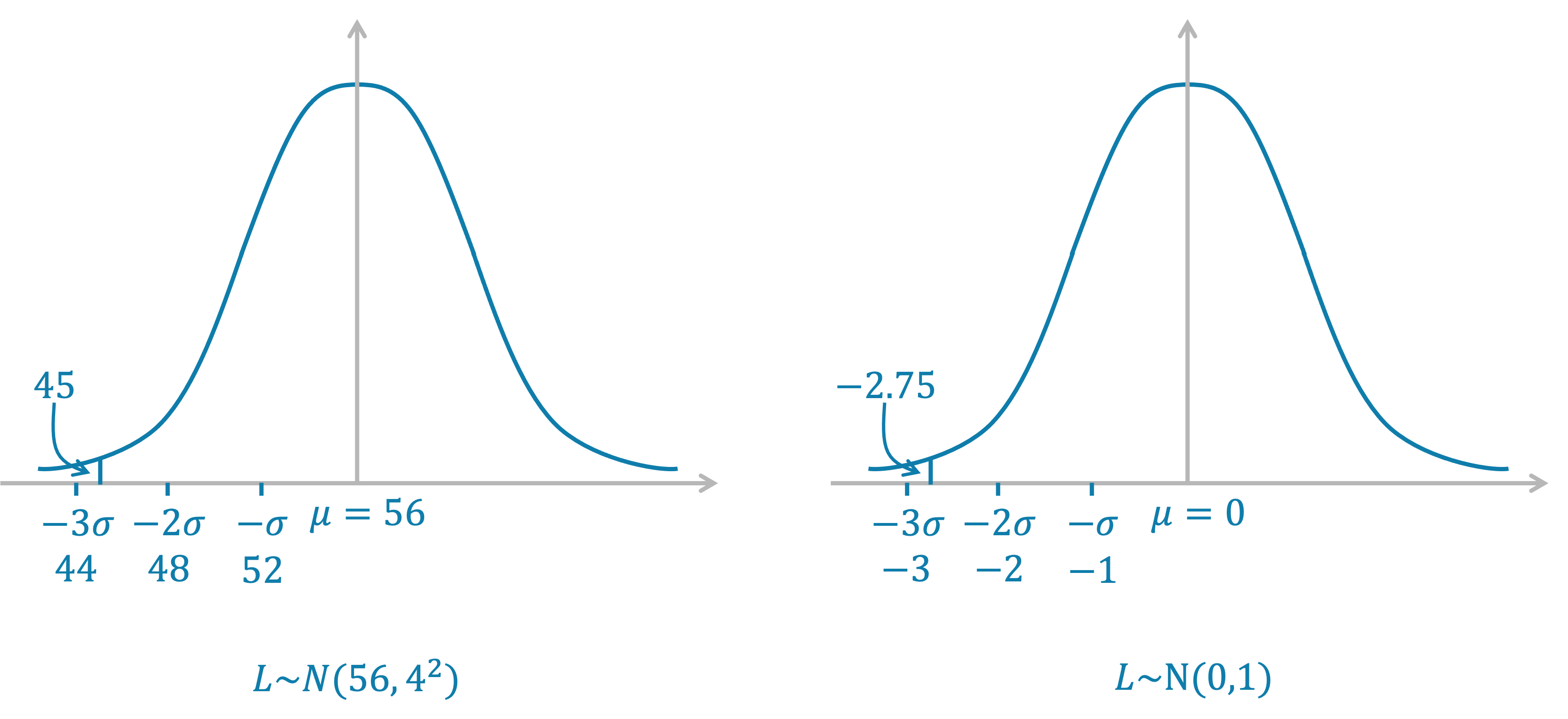
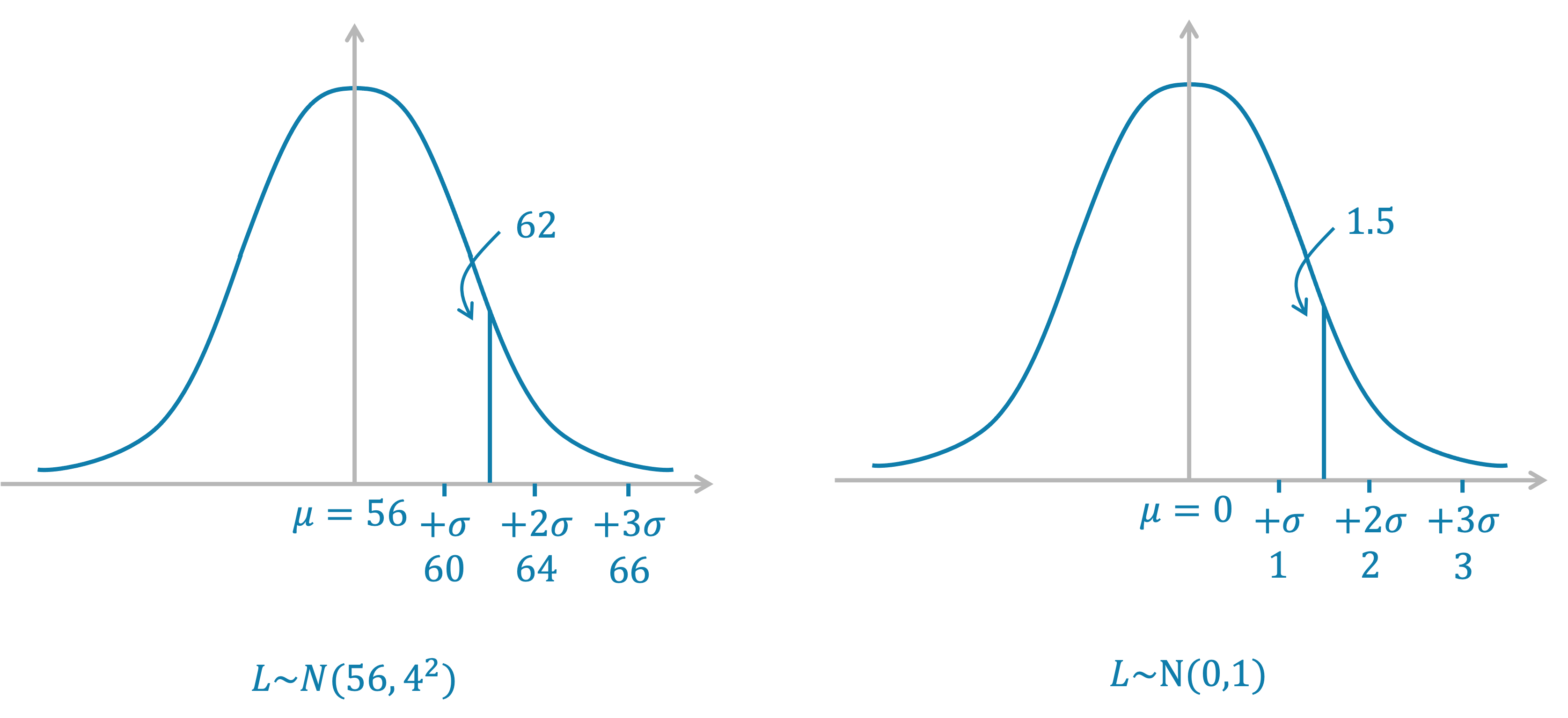
The length of a population of cats is normally distributed, with mean 56 cm and standard deviation 4 cm.
(a) Find the z-values of
(i) 45 cm
Answer:
Find the z-value of 45 cm using the relationship
A sketch of the standard normal distribution compared to the original distribution would therefore look like this
(ii) 62 cm
Answer:
Find the z-value of 45 cm using the relationship
A sketch of the standard normal distribution compared to the original distribution would therefore look like this

Unlock more, it's free!
Did this page help you?