Interest Rates & Saving (AQA Level 3 Mathematical Studies (Core Maths))

What is interest?

• Interest is money that is regularly added to an original amount of money

  • This could be added yearly, monthly, etc

  • When saving money, interest helps increase the amount saved

  • With debt, interest increases the amount owed

Simple Interest

What is simple interest?

• Simple interest refers to interest which is based only on the starting amount

  • Each interest payment (or charge in the case of debt) will be the same

• To find the total simple interest earned

  • Find a percentage (the percentage rate) of the starting amount

    • Use a multiplier to do this, (e.g. 0.05 to find 5%)

  • Multiply this by the number of time periods, (e.g. years), it is being applied for

• To find the total amount (or balance) after the simple interest has been earned

  • Use the same method as above, and add this on to the starting amount

Compound Interest

What is compound interest?

• Compound interest is where interest is calculated on the running total, not just the starting amount

  • This is different from simple interest where interest is only based on the starting amount

• E.g. $100 earns 10% interest each year, for 3 years

  • At the end of year 1, 10% of $100 is earned ($10)

    • The total balance will now be 100+10 = $110

  • At the end of year 2, 10% of $110 is earned ($11)

    • The balance will now be 110+11 = $121

  • At the end of year 3, 10% of $121 is earned ($12.10)

    • The balance will now be 121+12.1 = $133.10

How do I calculate compound interest?

• Compound interest increases an amount by a percentage, and then increases the new amount by the same percentage

  • This process repeats each time period (yearly or monthly etc.)

• We can use a multiplier to carry out the percentage increase multiple times

  • To increase $300 by 5% once, we would find 300×1.05

  • To increase $300 by 5%, each year for 2 years, we would find (300×1.05)×1.05

    • This could be rewritten as 300×1.05²

  • To increase $300 by 5%, each year for 3 years, we would find ((300×1.05)×1.05)×1.05

    • This could be rewritten as 300×1.05³

• This can be extended to any number of periods that the interest is applied for 

  • If $2000 is subject to 4% compound interest each year for 12 years

  • We would find 2000×1.04¹², which is $ 3202.06

  • Remember to round your final amount to 2 d.p.

• Note that this method calculates the total balance at the end of the period, not the interest earned

  • To find just the interest earned, find the difference between the total balance and the original amount

• This method can be summarised as a formula if preferred

  • After years,

  • at an annual interest of (where is a decimal),

  • an amount will have grown to:

    • 

How do I find the number of years to reach a particular balance?

• To work out the number of years, , required to reach a particular balance, use the same equation structure as when finding a balance with a known number of years

• Suppose £4000 is invested at 5% per year, and we are required to find how many years it takes to accumulate a balance of at least £6000

  • Using the same structure as when finding the balance, we can write

    • 

  • The quickest way to find is by using trial and error

    • , not larger than 6000 at the end of 6 years

    • , not larger than 6000 at the end of 8 years

    • , larger than 6000 at the end of 9 years

  • At the end of 9 years the balance will be larger than £6000

AER (Annual Equivalent Rate)

Why is AER useful?

• AER (Annual Equivalent Rate) is used to compare different savings accounts across a year, taking into account differences in interest rate and payment intervals

• Different savings accounts will pay interest at different intervals

  • This is usually either annually or monthly

• Earning 12% interest, paid at the end of 1 year, will result in a different balance to earning 1% interest, paid monthly (12 times per year)

  • Consider a balance of £100 paid 12% at the end of 1 year

    • £100 × 1.12¹ = £112

  • Consider the same balance subject to 1% interest, 12 times through the year

    • £100 × 1.01¹² = £112.68

    • This is equivalent to an Annual Equivalent Rate of 12.68%

• AER is used so that the different interest rates and payment intervals can be incorporated into a single figure for easier comparison

How do I calculate AER?

• The formula for AER is given on the formula sheet in your exam

  • The annual effective interest rate (AER), , is given by

    • 

    • is the nominal interest rate

    • is the number of compounding periods per year

    • The values of and should be expressed as decimals

• To find the AER for a savings account paying 6% interest each month

  • is 0.06 (6% as a decimal)

  • is 12 (paid monthly, 12 payments per year)

  • 

  • The AER is therefore 6.17% (to 2 decimal places)

• Notice that the AER for an account paying interest annually will be equal to

Savings & Investments

What are the differences between savings and investments?

• Savings are money stored in an account with a known and guaranteed rate of interest

• Investments are money that is spent on something that has value, in the hope that its value will increase, but the value could also decrease

• The key difference is the level of risk involved

  • Savings provide a predictable and secure return on the starting amount

  • Investments include a risk that money may be lost, but the maximum returns could be much higher than a savings account

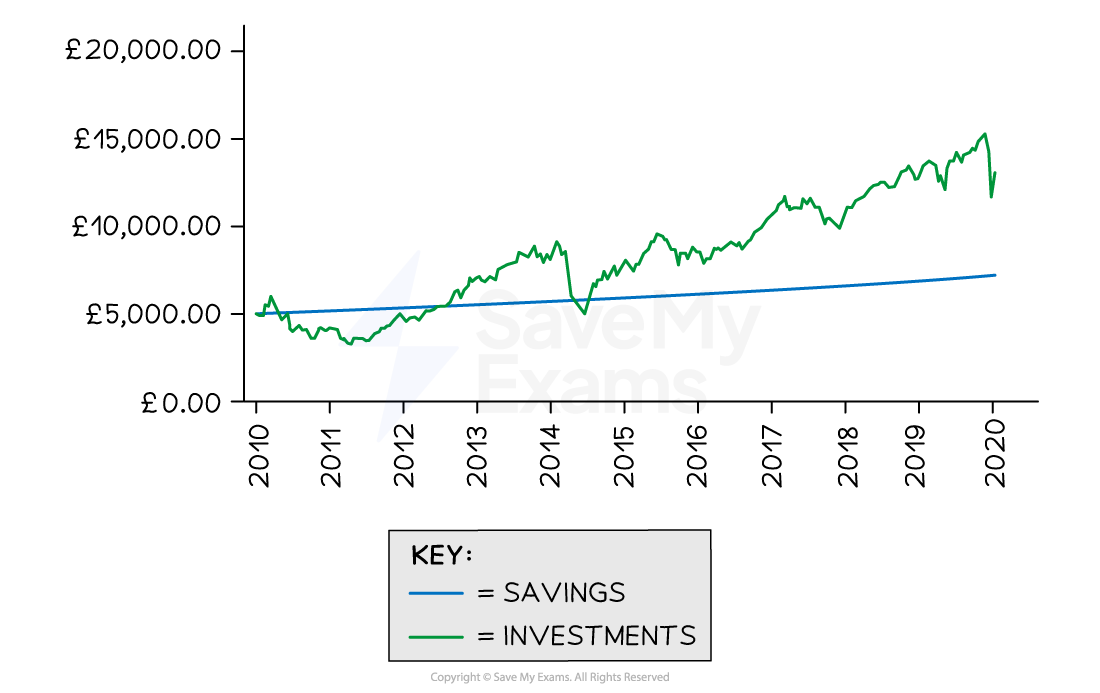
• The graph below shows how £5000 could grow when in a savings account, compared to being invested

  • In this example the value of the investment increases overall, which is never guaranteed

  • There are several points on the graph where the value of the investment is lower than if it had been placed in a savings account

Advantages and disadvantages of savings and investments