GCSE Maths Formulae Sheets: Your Essential Preparation Guide

The exam boards (AQA, Edexcel and OCR) will again be providing formulae sheets for the GCSE maths exams to be sat in 2024. This article provides a brief guide to what is on the sheets and how to use them.the GCSE maths exams to be sat in 2024. This article provides a brief guide to what is on the sheets and how to use them.

What is a GCSE Maths Formulae Sheet?

There are a number of mathematical formulas you might need to use to answer the Questions on a Maths GCSE Exam. Normally you would be expected to memorise these.

• However, following disruptions to education due to Covid, formulae sheets containing some of these formulas were provided for students sitting the exams in 2022 and 2023

• It has been decided to provide these sheets again for Maths GCSE exams in 2024

• This is the last year that this will happen – in 2025 things will go back to the pre-Covid arrangements, and formulae sheets will not be provided

It’s important to note that not every formula you need will be on the formulae sheet. But because you don’t need to memorise the ones that are on the sheet, it should make your exam preparation a bit easier.

What Formulas are on the GCSE Maths Formulae Sheet?

All three exam boards will be providing the exact same formulas on their exam formulae sheets. These are listed below, broken into the three main types:

Algebraic formulas

• The compound interest formula
  Total accrued

  • The variables in the formula:

    • P is the principal amount (i.e. the amount originally invested)

    • r is the interest rate (so if the interest rate is 4%, put a 4 here)

    • n is the number of times the interest is compounded (often this will be the number of years, but read the question carefully to make sure)

  • A common example of using this would be to find how much money is in a savings account after an amount P is invested at an interest rate of r % per year for a total of n years

• The “OR” probability formula
  P(A or B) = P(A) + P(B) – P(A and B)

  • P(A) is the probability of outcome A occurring, and P(B) is the probability of outcome B occurring

  • This formula can be used to find any one of the four probabilities if you know the other three

    • Substitute in the values you know, and solve for the one you want to know

• The “AND” probability formula (Higher tier only)
  P(A and B) = P(A given B) P(B)

  • P(A given B) is the probability of outcome A occurring given that outcome B has occurred

    • Note that the two probabilities on the right-hand side are multiplied together

  • This formula can be used to find any one of the three probabilities if you know the other two

    • Substitute in the values you know, and solve for the one you want to know

• The quadratic formula (Higher tier only)
  

  • This is used to find the solutions to the quadratic equation
    

  • Remember there are other ways to solve a quadratic equation (e.g. factorising)

    • The quadratic formula will always work, but may be slower than other methods

    • If the question tells you to round your answer, then the quadratic equation will probably have to be used

Geometric formulas

• The area of a trapezium formula
  Area of a trapezium =

  • The variables in the formula:

    • a and b are the lengths of the parallel sides

    • h is the height (i.e. the perpendicular distance between the parallel sides)

  • A trickier question might give you the area and ask you to find one of the other values 

    • Substitute in the values you know, and solve for the one you want to know

• The volume of a prism formula
  Volume of a prism = area of cross section × length

  • You may need to calculate the length or the area of cross-section before using the formula

  • A trickier question might give you the volume and ask you to find one of the other values 

    • Substitute in the values you know, and solve for the one you want to know

• The circumference and area of a circle formulas
  Circumference of a circle = 2π r = πd
  Area of a circle = π r² 

  • The variables in the formula:

    • r is the radius of the circle

    • d is the diameter of the circle 

    • π is the mathematical constant pi

  • Either formula can be used for the circumference

  • For the area you have to use the radius – look out for questions where you are given the diameter instead

  • A trickier question might give you the circumference or the area and ask you to find one of the other values 

    • Substitute in the values you know, and solve for the one you want to know

Trigonometric formulas

• Pythagoras’ Theorem formula
  a² + b² = c²

  • The variables in the formula:

    • c is the length of the hypotenuse (longest side)

    • a and b are the lengths of the other two sides

  • This only works for a right-angled triangle

  • To find the hypotenuse use

    • To find another side use

• SOHCAHTOA formulas
  

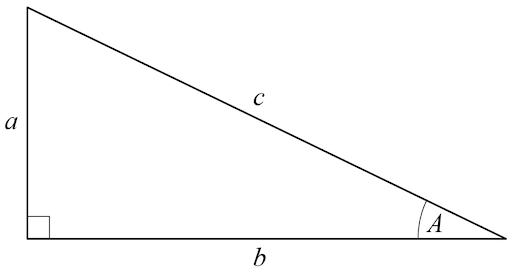
• These only work for a right-angled triangle

• You may need to relabel the sides and angles of the triangle to use these versions of the formulas

• To find an angle, use sin^-1, cos^-1 or tan^-1 on your calculator

• You may be used to these versions of the formulas instead:
  

  • θ is the angle, O is the opposite side, A is the adjacent side, and H is the hypotenuse

  • You can still use those versions of the formulas if you are more confident with them

  • But they are not on the formulae sheet, so you’ll need to remember them

• Non-right-angled trigonometry formulas (Higher tier only)
  sine rule:
  cosine rule:
  Area of a triangle =

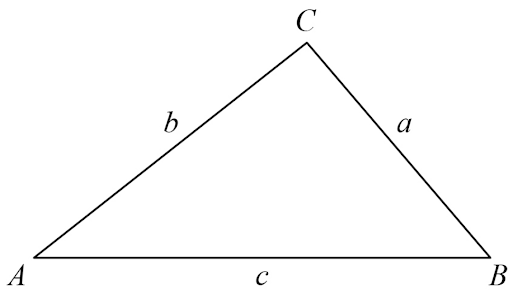
• These formulas work with any triangle (right-angled or not right-angled)

• You may need to relabel the sides and angles of the triangle to use these versions of the formulas

• To find an angle, use sin^-1 or cos^-1 on your calculator

• Remember the sine rule formulas are also valid if you “flip them over”:

Exam Board Maths Formulae Sheets

AQA GCSE Maths formulae sheets

• The official AQA Maths GCSE formulae sheets for the 2024 exams may be found here:

  • Maths GCSE AQA: Foundation Tier Formulae Sheet

  • Maths GCSE AQA: Higher Tier Formulae Sheet

OCR GCSE Maths formulae sheets

• The official OCR Maths GCSE formulae sheets for the 2024 exams may be found here:

  • Maths GCSE OCR: Foundation Tier Formulae Sheet

  • Maths GCSE OCR: Higher Tier Formulae Sheet

Edexcel GCSE Maths formulae sheets

• The official Edexcel Maths GCSE formulae sheets for the 2024 exams may be found here:

  • Maths GCSE Edexcel: Foundation Tier Formulae Sheet 

  • Maths GCSE Edexcel: HiEdexcel GCSE (9-1) Mathematics: Higher Tier Exam Aidgher Tier Formulae Sheet 

How to Use a GCSE Maths Formulae Sheet Effectively

Here are a few tips for making the most of the formulae sheets for your 2024 Maths GCSE exams

• The most important thing is to know what is and isn’t on the formulae sheets

  • Print out a copy of the official version of the sheet for your exam board and keep it with you when you revise

  • Practise using it when you work through past papers

• You don’t need to remember the formulas on the formulae sheet, but you do need to know how to use them

  • This includes knowing what all the letters in the various formulas mean

  • And how to rearrange a formula to solve for any value in the formula

• For the trigonometry formulas you will often need to relabel the triangle given in an exam question

  • This is to make sure that the letters for its sides and angles match the ones in the formula

Common mistakes to avoid when using the formulas on the formulae sheets

Here are a few common errors that occur with the formulas on the formulae sheet

• Using diameter instead of radius in the circle formulas (or vice versa)

  • Remember that radius is half the diameter (or diameter is two times the radius)

  • Make sure to use the right value for the formula you are using

• Entering the quadratic formula incorrectly in your calculator

  • You need to put brackets around any negative numbers you are substituting into the formula

    • But it’s safest to put brackets around all the numbers you are substituting

    • For example to solve , type this into your calculator:
      

• Attempting to use Pythagoras’ Theorem or the SOHCAHTOA formulas for a non-right-angled triangle

  • Remember, those formulas only work for right-angled triangles

  • But also remember when you do see a right-angled triangle in a question, to be suspicious that Pythagoras or SOHCAHTOA may be involved –  a question won’t always tell you that you have to use those formulas

Summary

The good news is that for your GCSE maths exams in 2024 you will be provided with a formulae sheet containing some of the most important formulas needed for the exam. This means you can spend less time memorising things, and more time working on your understanding and problem-solving skills.

Once you have printed out a copy of your exam board’s formulae sheet for your tier (Foundation or Higher), you can start practising exam-style questions right away using Save My Exams’ GCSE maths topic question banks:

• AQA GCSE Maths Topic Questions

• OCR GCSE Maths Topic Questions

• Edexcel GCSE Maths Topic Questions

• Edexcel GCSE Maths (Foundation) Topic Questions

Or if you want to revise your GCSE Maths topics a bit first before starting on the questions, have a look at our exam-board-specific revision notes here:

• AQA GCSE Maths Revision Notes

• OCR GCSE Maths Revision Notes

• Edexcel GCSE Maths Revision Notes

• Edexcel GCSE Maths (Foundation) Revision Notes