How can I best solve Mathematical Questions in my GCSE Physics exams?

Converting between units

Using the correct units is simple and can easily gain you an extra mark in a question. In physics, you must use standard scientific units, often called SI units. You need to remember the following units for GCSE physics:

• metre (m) – unit of length

• kilograms (kg) – unit of mass

• second (s) – unit of time

• ampere (A) – unit of electrical current

• kelvin (K) – unit of temperature

Sometimes non-standard units are given in a question. When this is the case, you should convert all the units you need into standard units. For instance, all lengths should be in metres and all measures of time (no matter how long) in seconds. Remembering the following conversions between commonly used units can save you time in the exam:

• 10 mm = 1 cm

• 100 cm = 1 m

• 1000 g = 1 kg

• 1000 cm³ = 1 L

• 60 s = 1 minute

• 60 minutes = 1 hour

In this worked example the units of mass have been converted from grams into kilograms and the units of length from centimetres to metres

Listing known quantities and choosing an equation

In order to find the unknown variable or unknown quantity in a question, you need to figure out which equation to use. Listing all the known quantities will help you to do this. It can take time, but it will help you to pick up marks.

This mark scheme lists all the known quantities

Once you have listed the known quantities, you can use the equation booklet or sheet (if you have one in your exam) and your physics knowledge to select the correct equation for the calculation. The correct equation will be the one in which all the variables are known, except one. The unknown variable is the one you need to find to answer the question. Sometimes missing values may come from previous question parts, so look out for that too. 

In this example, u, v and t are known, and x is the one unknown variable. From this, the correct equation is chosen

Rearranging Equations

Once you have listed the correct values with the correct units and have identified the most suitable equation, you might need to rearrange the equation to make the unknown variable the subject. This can be quite tricky because there are lots of rules and patterns, but essentially you want to rearrange or move everything around in the equation so that the unknown quantity is by itself on one side of the equals sign. This is also called changing the subject of the formula – the subject is the quantity you need to find).

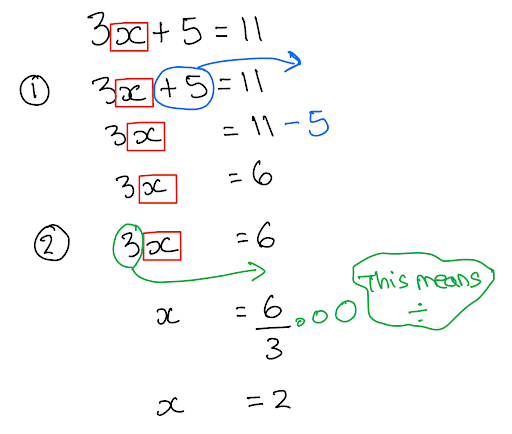
In this example, 3x + 5 = 11 is rearranged to make x the subject. The first step is moving the + 5 and then the 3

Remember that each operation to rearrange the equation must be applied to both sides of the equation. It may not always be clear that this is happening – as in the example above. The correct mathematical method is shown below.

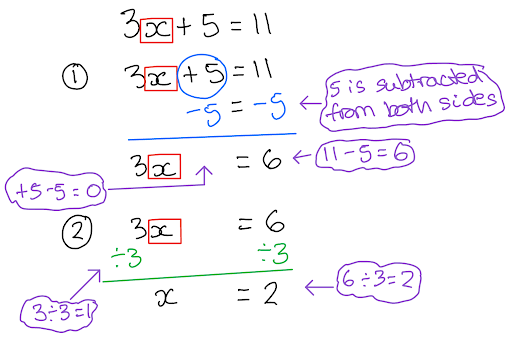
In this example, the + 5 has been reversed and subtracted from both sides and the x 3 has been reversed and divided from both sides

To rearrange equations you need to perform the reverse operation of the operation linked to the number. The reverse or opposite operation of:

• multiply is divide

• subtraction is addition

• squaring a number is finding its square root.

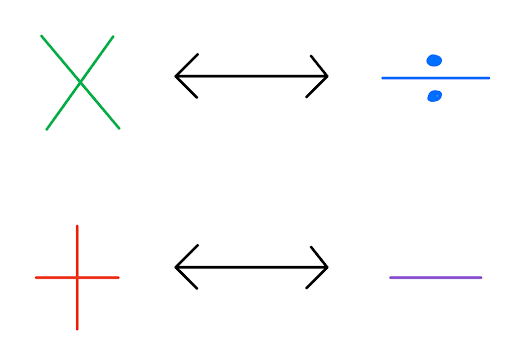
The reverse or opposite operation of divide is multiply and of subtraction is addition

Each number in an equation has an operation attached to it. (This is the operation that needs to be reversed in order to rearrange the equation.) In the example below, the 7, 5 and the y are positive. You don’t need to write this down but you should be aware of it because their sign is not indicated. The 7 is x 7 and the 5 is x 5 and the 1 is −1. It is a good idea to use brackets to group each number with its operation. The y represents a number value that can be found by rearranging this equation.

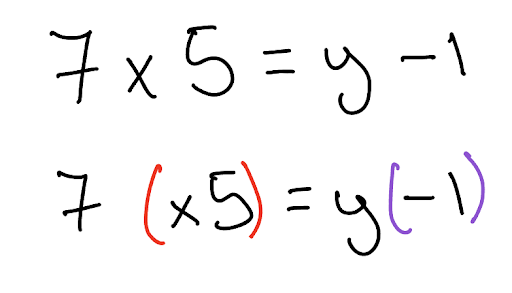
In this example, the x is attached to the 5 and the − to the 1. 7, 5 and y do not have a sign so they must be positive

Some equations are known as one-step equations and require just one move to make the correct variable the subject. In the example below, dividing both sides of the equation by mass, m, will make acceleration, a, the subject – alone on one side of the equation.

In this example of a one-step rearrangement, F = ma is rearranged to make a the subject. To do this, both sides are divided by mass, m

In some instances, it may take several steps to rearrange an equation. When this is the case, you should start further away from the subject and work inwards by reversing the operations in order of BIDMAS or BODMAS

• Addition and subtraction first

• Then multiplication and division

• Then indices or powers

• Finally, remove the brackets 

• Continue rearranging as per this order until only the unknown variable is alone on one side of the equation

Rearranging the kinetic energy equation to make velocity, v, the subject is one of the most difficult rearrangements you might have to make. There are many steps involved, as well as a square root sign. You can see from the example below that the ½ is moved first because it is furthest away from the v.

The example of a multi-step rearrangement shows how to rearrange the kinetic energy equation to make velocity, v, the subject. Start by multiplying both sides by 2, then divide both sides by m and finally take the square root of both sides

Substituting into Equations

Once you have your quantities in the correct units, you need to substitute them correctly into an equation. Improving your confidence in this skill will allow you to pick up a lot more marks in the exam. Remember that substitution in maths is the same as substitution in football (and in physics). You can use the methods explained in the Save My Exams GCSE maths revision notes but see below where these skills are linked more specifically to physics questions.

In football, the player is replaced with another player, just as one quantity is replaced by a number value in maths and physics

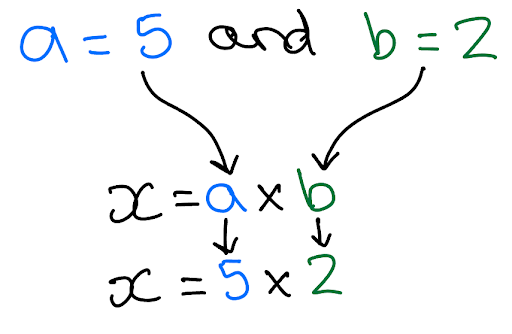
In the equation x = a × b the number 5 replaces the letter a and the number 2 replaces the letter b

The trick to making a correct substitution is: 

1. Highlight the known quantities (numbers) in the question.

2. Use the correct equation.

3. Place these values into the equation.

In the worked example below, the question asks for the density of the block: 

1. The volume of 24 m³ and the mass of 2.4 kg are highlighted. 

2. The density equation is stated: density = massvolume.

3. 24 and 2.4 have been substituted into the correct places in the equation.

A Worked Example Showing Substitutions

Mass and volume are substituted into the equation for density: 24 replaces the volume and 2.4 replaces the mass

Fractions and Proportionality

Once you have substituted values into your equation you can save a lot of time if you can interpret fractions and proportional relationships quickly without a calculator. It is easy to forget that the bigger the denominator the smaller the fraction. For example, 6 > 2 but 16<12.  

The number on top of a fraction is the numerator and the number on the bottom is the denominator. This principle applies to any fraction. 

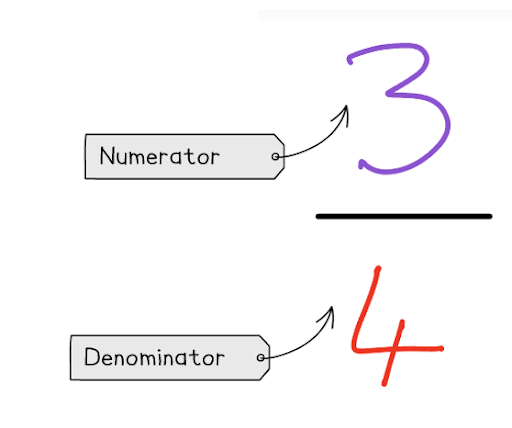
The numerator and denominator of a fraction

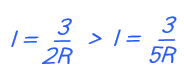
Here the current with the smaller denominator (2R) is larger than the current with the bigger denominator (5R)

Sometimes doubling one quantity in an equation will also double the final answer. In the example below, the total resistance of the second circuit is double the resistance of the first circuit. This means the potential difference will be double because V is proportional to R. If you notice that, then you don’t need to write out all the workings shown.

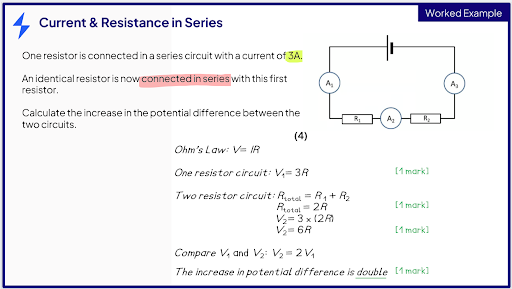
V = IR so when R is doubled then V is also doubled if I remains the same

Conclusion

This article has given you an overview of the tools you need to solve mathematical questions in your GCSE physics exam. The best preparation you can do now is practice! Use the exam specific topic questions on the Save My Exams website to do this. Start with the easy questions, using the revision notes to help you, and work your way up to the hard questions. Each topic contains a selection of problems that best represent the type of questions you are likely to see in your exam.