GCSE Maths Algebra Revision: Tips, Tricks, and Examples

Published

10 June 2024

Read time

8 minutes

Contents

Have you noticed how Algebra gets a bad reputation in the real world? A lot of people find it tricky. After teaching Maths GCSE for ten years — and with a PhD in Maths — I love Algebra and want to share my top tips, tricks and examples to help you with your GCSE Maths Algebra revision.

Algebraic vocabulary

What are the differences between an equation, a formula, an expression and an identity? Take a look at my simplified table to help.

	Example	What are they?	What can you do with them?
Equation	2x + 1 = 5	A statement where the left-hand side and right-hand side are equal	Solve them to find x
Formula	y = mx + c	A worded rule, definition or relationship written in letters for shorthand	Substitute values into them
Expression	2x + 1	A collection of terms and numbers with no equals sign	Simplify, expand, factorise or rewrite them, e.g. x + x + 1 (you cannot solve them)
Identity	x + x + 1 ≡ 2x + 1	A different way to write an expression that works for any value of x (it has a 3-line equals sign)	Rewrite expressions and equations in a different form (you cannot solve them)

Common mistakes to avoid

The most common error I see is substituting negative numbers incorrectly into expressions.

For negative numbers, always use brackets followed by BIDMAS/BODMAS. For example:

Substitute x = -2 into 5x²
- Correct: 5 × (-2)² = 5 × 4 = 20
- Incorrect: 5 × -2²= 5 × -4 = -20
- Incorrect: (5×-2)²= (-10)² = 100
- Incorrect: (5×-2)²= -10² = -100

Beware: your calculator can confuse you! If you type -2² you get -4, but the square of -2 is positive 4, not negative 4. You need to type in the brackets, (-2)², to get the correct answer.

Another common mistake is expanding brackets. For example:

Solve (x + 3)²
- Correct: (x + 3)(x + 3) — expand using FOIL then collect like terms to get x² + 6x + 9
- Incorrect: x² + 3² to get x² + 9

I have seen a lot of students who know this common error still get quadratic simultaneous equations wrong, for example when substituting y = x + 3 into x² + y² = 9, and then squaring incorrectly!

What are algebraic fractions?

$\frac{4 x + 6}{2 x^{2} - 7 x - 15}$

Algebraic fractions are fractions which have algebra in either the numerator, denominator or both.

Here’s my trick for algebraic fraction questions in the exam: think of them as factorisation questions instead. If you factorise top and bottom, you can then cancel any common brackets.

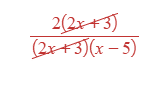
I have seen a lot of students get zero marks in these questions because they try to cancel individual terms. Remember to factorise first!

What are functions in algebra?

$f (x) = 10 - x$

A function takes an input, x, and creates an output, for example 10 - x.

I have seen a lot of students getting the notation wrong. For example, an input of 2 gives an output of 8:

Correct: f(2) = 8
Correct: f(2) = 10 - 2 = 8
Missing information: f(x) = 8 (what is the input, x?)
Incorrect: f(x) = 2
Incorrect: 10 - x = 2
Incorrect: anything involving f(8)

I have a silly way of remembering function notation: by imagining the brackets as a mouth. The function “eats” the input, f(2), and spits out the output, f(2) = 8.

Another common mistake I see with functions is being given information in the question and not knowing whether to substitute or solve.

Below are two examples to highlight this.

f(x) = 10 - x

Example

Operation

Notation

Given input

x = 7

Substitute

f(7) = 10 - 7 = 3

Given output

f(x) = 4

Replace f(x) with:

10 - x

Then solve

10 - x = 4

10 - 4 = x

so x = 6

What is algebraic proof?

Algebraic proof is when you use algebra to prove a statement. For example, “prove that the sum of two even numbers is even”.

My advice for these questions is to over explain, not under explain. Don’t assume lines of working are “obvious” - examiners will want to see them.

My tip for writing an easy conclusion is to copy the exact wording from the question.

For example:

Question

Prove that the sum of two even numbers is even

Marks

Under-explained answer

2n + 2m so it is even

1/3

Over-explained answer

Let n and m be integers

2n and 2m are even integers

The sum of 2n and 2m is 2n + 2m

This factorises to 2(n + m)

This is 2 x “an integer” so it is even

Therefore the sum of two even numbers is even

3/3

Graphs in Algebra

It is possible to do a graph-based question without ever drawing its graph. For example, finding the equation of a line perpendicular to another line.

However, there is always at least one question on the exam paper that requires solving an equation using a graph. My advice here is to not confuse the graph’s equation with the equation you want to solve!

For example, if asked to use the graph of y = x² + 4 to solve x² + 2x - 1 = 0, I would tell my students to identify which equation “does not have a y” in it, because this equation is:

the one you want to solve, and
the one you can rearrange to look like the other.

So x² + 2x - 1 = 0 rearranges to x² + 4 = -2x + 5, meaning you plot y = -2x + 5 on the graph of y = x² + 4 and read off the x-intercepts.

What is problem solving in algebra?

Problem solving means you are given a real-life (or made-up) situation, called a context, and you are expected to form and solve an equation to answer any questions asked.

I always tell my class to imagine that there are 2 marks in the exam for just reading the context carefully! Taking your time at the beginning can often reduce your total time taken.

When forming equations, I advise students to bring all terms to one side to see if it is a quadratic, in the form ax² + bx + c = 0.

Also, remember to relate any answers back to the context, such as the answer below on the length of railway track needed for a project.

	Answer
Not related to the context	x = 7.25
Related to the context	The total length of track needed is 7.25 km, correct to 3 significant figures.

What is the hardest topic in GCSE Algebra?

In my experience, completing the square is one of the hardest methods for students to understand in algebra.

I like to think of it as forcing an expanded quadratic expression, x² + bx + c, into a “bracket squared”:

(x + p)² where p is half of b

But that “bracket squared” often needs “completing” to make both expressions equal, giving:

(x + p)² - p² + c

This has now completed the square! My summary table is:

Expanded form

Completed-square form

Example

x² + bx + c

(x + p)² - p² + c

p is half of b

x² + 10x + 1

p = 5

(x + 5)² - 25 + 1

giving (x + 5)² - 24

ax² + bx + c

a(x + p)² - ap² + c

p is half of b/a

3x² + 12x + 1

a = 3

p = half of 12/3 = 2

3(x + 2)² - 3×2² + 1

giving 3(x + 2)² - 11

GCSE Algebra: Nail your exams

With the tips, tricks and examples above, you should now be in a stronger position to nail the algebra questions in the exam.

Below are links to revision resources at Save My Exams for the topics mentioned above. In fact, Save My Exams covers the whole GCSE Maths syllabus, so be sure to take a look!

Here at Save My Exams, we develop high-quality, affordable revision resources; consider signing up for a Save my Exams subscription to help you get the most out of your revision. We support over 1.5 million students each month in preparing for their exams and achieving successful results, we’d love to help you too.

Sign up for articles sent directly to your inbox

Receive news, articles and guides directly from our team of experts.

Share this article