Foundation GCSE Maths Revision Notes: master the basics, ace the exam

Foundation GCSE Maths Revision Notes: master the basics, ace the exam 

Mastering the fundamentals of mathematics is essential for confidence and success in your Foundation GCSE Maths exam. This guide explores key areas in the Foundation GCSE Maths that are essential to get to grips with, alongside some useful exam and revision tips. Along the way I’ll highlight topics that can prove tricky and give you some hints and tips on how to overcome problems to help you to ace your exams!

What should you revise for Foundation GCSE Maths?

All Foundation GCSE boards (Edexcel, AQA, OCR and WJEC) cover the main areas of Number, Algebra, Geometry, Statistics and Probability. So let’s take a look at some of the topics within those areas that are essential to master!

Number and Operations

Number is the cornerstone of mathematics and having a good sense of place value, basic operations and types of number is absolutely critical as they form the basis of all of the other maths that you study.

You need to be fluent in the different number operations: addition, subtraction, multiplication and division. In these, multiplication and division often cause the biggest issues for people, particularly when they incorporate decimals. However, they are almost certain to pop up in the non-calculator paper. Luckily there are a number of different methods that you can use to perform these calculations, e.g. the lattice method, grid method or column method for multiplication, and it’s often a case of finding the method that suits you best. 

Factors, multiples and primes is another area that always pops up in an exam paper and the main difficulty that students often experience is confusion between the meaning of the different terms. If you have trouble remembering definitions, why not try creating some flashcards with the term on the front and the definition on the back and have someone test you on it? Or it could help you to use a visual techniques to remember the meaning of different words:

Another couple of topics in Number that often cause difficulties for students are basic fractions and converting between fractions, decimals and percentages. Make sure that you go back to basics to understand the concepts thoroughly and then try to come up with a strategy for remembering the procedures for different operations with fractions and converting between types of numbers.

Algebra

The second major area covered in your Foundation GCSE Maths course is algebra. Language in algebra is very specific and you need to be clear on algebraic notation and vocabulary. Make sure that you have revised and know the definitions of the following key terms: expressions, equations, formulas and inequalities. 

Sometimes the abstract nature of algebra can also make students feel uncertain about things that they are really secure about when it comes to real numbers. Therefore a top tip is that if you are unsure about something, see if you can think of a real number example instead, which is comparable, and try to work out how you can apply the steps you did with the number example to the algebraic example.

Another big challenge faced by students in an exam is with more complex problem-solving questions that involve a lot of language, these also often require the use of algebra. For example, consider the problem below:

“Sharon has double the number of sweets that Josephine has.

Martin has 8 fewer sweets than Sharon.

The total number of sweets between the three of them is 27.

Find the ratio of Martin to Josephine to Sharon for the number of sweets that each of them has.”

This question demonstrates a number of skills that you should practise to ensure that you can tackle wordy questions successfully. You need to be able to:

• convert written statements into an algebraic expressions, (e.g., Sharon has double the number of sweets that Josephine has, S = 2J) 

• identify keywords that imply what you need to do, (e.g., “total” implies that you need to add the expressions together) 

• and look carefully for any clues about the form in which the final answer should be given, (e.g., the word ratio tells you the form for your final answer)

Geometry and Measures

Moving onto geometry and measures, one of which is visualisation. This is a topic area that requires working in both 2D and 3D situations and often involves being able to “see” what the situation looks like. Being able to sketch out diagrams, even if it’s not asked for or required, can really help you with this, as It helps you to pick out key information from the text, which often in turn then helps you to solve a problem more easily. A diagram doesn’t need to be drawn perfectly or to scale, a quick, annotated sketch, such as in the example below, can make a wordy question much easier to solve.

“The length of one side of a rectangle is 12 cm.

The length of the diagonal of the rectangle is 13 cm.

Calculate the area of the rectangle.”

A lot of memorisation is also required in this area of maths, with students having to recall and apply basic angle properties, angles in polygons, and angles in parallel lines. Creating flashcards for this particular topic area can help you to remember all of the different angle facts and how to phrase them. In an exam question you will only get full marks if you can find the appropriate angle and give the reason behind it, e.g. Angle BCD = 50º because angles in a triangle add up to 180º.

Applying all of these facts can also be quite tricky, particularly if you are given a complicated diagram. If you can’t see how to get to the final answer straight away, try annotating the diagram with any angles or lengths that you can work out using any facts that you know. Often finding out one piece of information will lead to another and so on until you end up finding out the information that you need in order to be able to answer the question!

Statistics and Probability

The final major area that is covered in the Foundation GCSE Maths course is that of statistics and probability. Here the biggest issues are often to do with diagrams. You need to be familiar with both drawing and interpreting a wide range of graphs, charts and diagrams from scatter graphs and pie charts to two-way tables and tree diagrams. 

Any diagram that you draw needs to be readable and accurate. You should draw diagrams large enough to be able to see the detail. When drawing any of these diagrams make sure that you show all of your working clearly, so that even if you do make a mistake the examiner can see that you have followed the correct process. For example, if you are asked to draw a pie chart, make it clear how you have calculated the angle for each section.

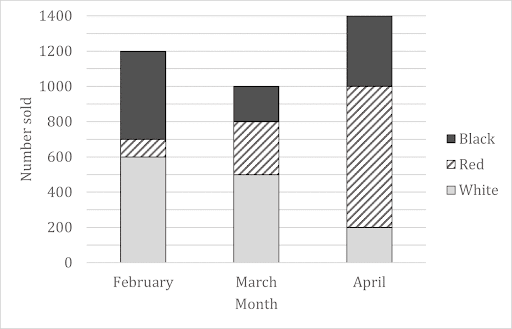
When interpreting graphs, you must be aware of the type of graph or diagram you are looking at and the type of information that it is showing. It’s important to make sure that you understand the context of the question so that you can identify and use the correct information from the diagram. For example in the graph below, it shows the number of cars of different colours sold each month. If you were asked to find the fraction of the total number of cars sold that were white, you would need to identify how many white cars were sold (add up the heights of the three bars shaded grey) and divide it by the number of cars were sold in total (the total height of all three bars)

Exam and revision tips: How to pass Foundation GCSE Maths

So now that we’ve taken a look at the main topic areas examined in the Foundation GCSE Maths, let’s explore some effective study strategies for your revision.

Revision Notes

A great way to start on your revision is to review your notes as a reminder of how to apply various mathematical skills etc. If you have gaps in your own notes, here at Save My Exams we have comprehensively written, course specific Foundation GCSE Maths Revision Notes to support you! Try working through the detailed worked examples that accompany the notes to see how those particular skills may be applied in context or making flashcards to help you remember key information or techniques.

Practice, practice, practice!

After a review it’s then onto the core part of maths revision - practice, practice, practice! It really is the best way to ensure that you have fully understood a particular concept and can apply your understanding to a range of situations. Our Foundation GCSE Maths Topic Questions are carefully split not only by topic but are also separated into three levels of difficulty, easy, medium and hard, so you can work on a topic at the level you need to.

Revise together

Although a lot of maths revision is likely to be done independently, a collaborative effort can also be extremely effective. They say that teaching something is the best way to learn it and from my experience I can support that statement! Why not team up with a study buddy and take it in turns to explain a concept or your solution to a particular problem? Alternatively, you could gain some brownie points with your parents by volunteering to help a younger sibling with their maths homework. 

Even if there is no one else around, don’t underestimate the power of speaking out loud to yourself. If you’re stuck on a particular problem, take the time to read the question aloud and to talk yourself through the steps that you have taken so far. When encouraging students to use this technique, I have frequently witnessed the “lightbulb moment”!

Mock exams and practice papers

After some sustained topic specific practice, it’s time to focus on past papers. You are likely to have already completed some mock exams in your final GCSE year at school and this will have given you a good sense of how the GCSE exam works, how long it is and what a paper looks like. 

In order to increase your confidence when it comes to the real exam, it’s worth going through several past papers independently and working on your exam technique. You can start just by taking as much time as you need to complete a past paper and using notes to help you with any problems you encounter. This will help you to get used to jumping around from topic to topic. After doing a couple of papers in this manner, you can ditch the notes and try to complete as much of it as you can with no additional support to really test your knowledge. Finally, working through past papers with no support and under timed conditions can really help you to find out how to pace yourself in the exam. 

Each time you complete a paper, make sure that you go through the markscheme with your answers to see where you will have gained or lost marks. Doing this each time will help you to become more familiar with the expectations that examiners have and enable you to realise what you need to do to gain more marks. Save My Exams has a whole host of Foundation GCSE Maths exam papers and their markschemes organised clearly so you can work through them one at a time.

Set yourself up for Foundation GCSE Maths success

Mastering the basics of the Foundation GCSE Maths course will be fundamental to success in your exam. By dedicating time to revising the core concepts in number, algebra, geometry, probability and statistics, you’ll build a solid foundation. Don’t let challenges discourage you, through consistent practice and the right mindset you’ll be well-equipped to ace your exam! And remember, at Save My Exam we have everything to help you on your way, including detailed Revision Notes, hundreds of Topic Questions and lots of Past Papers!