Motion Graphs (Edexcel International AS Physics)

• Three types of graph that are used to represent motion are displacement-time graphs, velocity-time graphs and acceleration-time graphs
• Graphs are named 'y-axis - x-axis', so 'displacement-time' simply means 'displacement on the y-axis and time on the x-axis'

• Graphs of motion can be thought of as telling a story of something which has happened in the real world, such as
  • the time, direction and average speed of a journey to school
  • initial and final velocity and acceleration as a rocket takes off from the launchpad
  • movement and speed in various directions as an athlete takes part in an event

• Interpreting graphs means using the slope of the line, or the area under the line to find information about that 'story'
• Drawing graphs is a skill where careful planning, plotting and line drawing from some data yields further information from an investigation

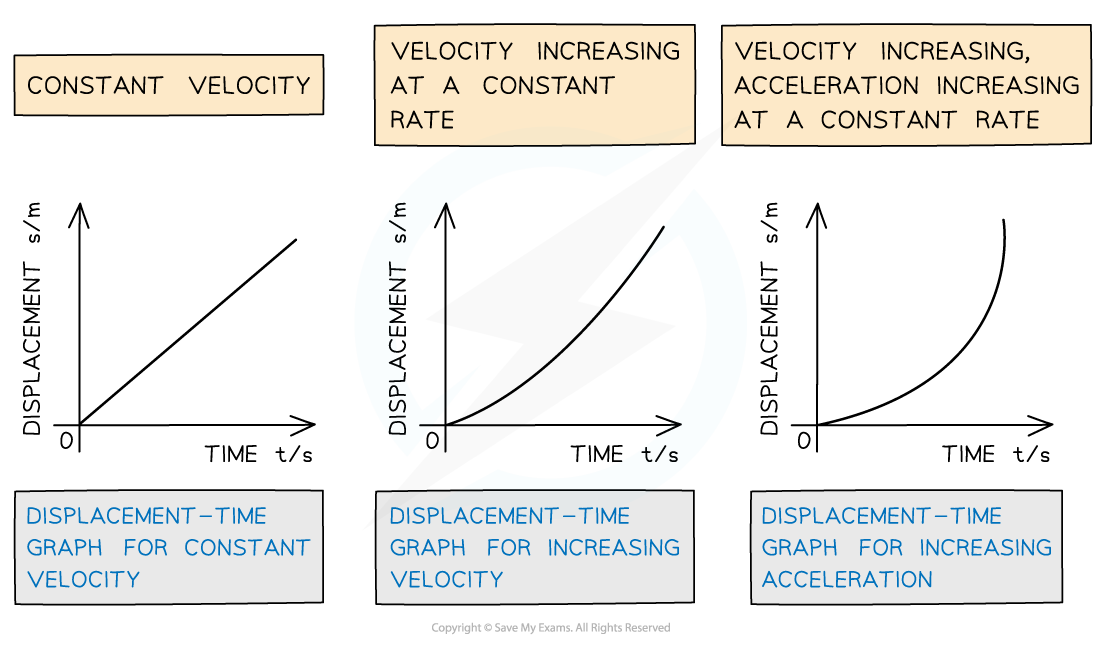
Displacement-Time

• On a displacement-time graph;
  • Slope equals velocity
    • A straight (diagonal) slope represents a constant velocity
    • A curved slope represents an acceleration
  • A positive slope represents motion in the positive direction
  • A negative slope represents motion in the negative direction
  • A zero slope (horizontal line) represents a state of rest
  • The area under the curve is meaningless

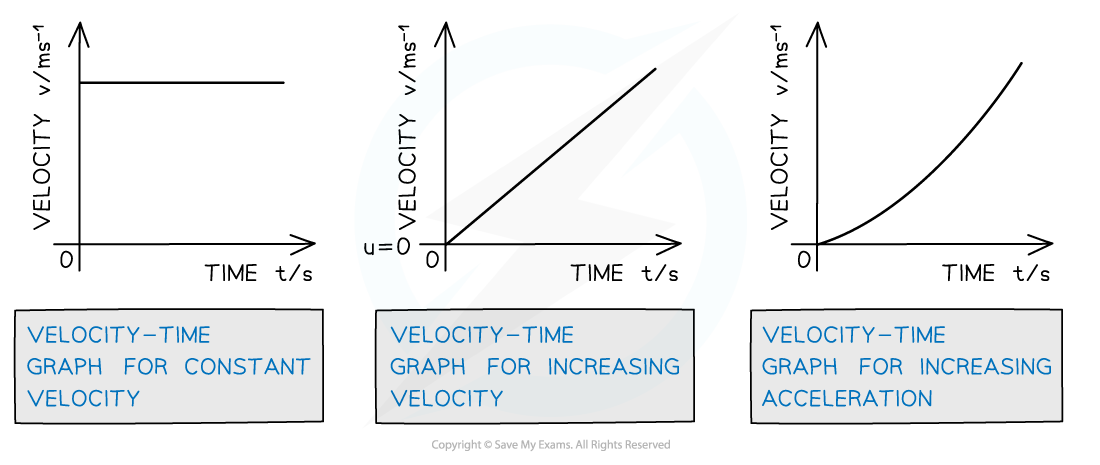
Velocity-Time

• On a velocity-time graph…
  • Slope equals acceleration
    • A straight line represents uniform acceleration
    • A curved line represents non-uniform acceleration
  • A positive slope represents an increase in velocity in the positive direction
  • A negative slope represents an increase in velocity in the negative direction
  • a zero slope (horizontal line) represents motion with constant velocity
  • The area under the curve equals the displacement or distance travelled

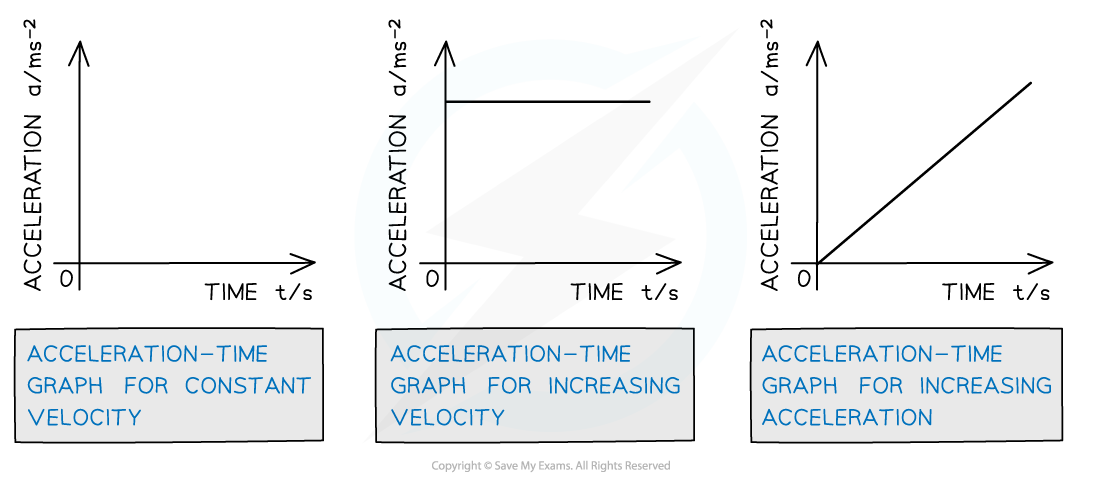
Acceleration-Time

• On an acceleration-time graph…
• A zero slope (horizontal line) represents an object undergoing constant acceleration
• The area under the curve equals the change in velocity
• The steepness of the slope is meaningless

• 

How displacement, velocity and acceleration graphs relate to each other

Drawing Graphs

• Drawing a good graph is an important skill

• Good graphs have the following:
  • Each axis has two labels; the name of the variable and the unit (and may include a multiplier, for  example, m × 10⁻⁹)
  • Values on the axes are evenly spaced, with the same number of divisions for each amount

• • The axes start at the origin only when this fits the data or the relationship being graphed is directly proportional or when specified in the question
  • Increments on the scale are in multiples of 2, 5 and 10 but never multiples of 3.
  • The range of values being plotted takes up the length of the axis, so that the plotted line takes up most of the space on the graph
  • Plots are accurate to within half a small square
  • Plots and curves are drawn with sharp pencil so that they are narrow (don't take up more than half a small square)

• • Lines of best fit match the data, so that lines go through as many of the plots as possible (ignoring outliers) with the remainder evenly spaced above and below the line

Part (a)

Step 1: Determine the direction of motion from the graph

• • Initially displacement increases from 0 - 50 m

• • This represents the sprinter running away from the starting position

• • Secondly displacement decreases from 50 - 0 m

• • This represents the sprinter returning towards the starting position

Step 2: Identify the sprinter's turning point on the graph 

• • The distance between the markers is from 0 → turning around point

• • This is 50 m from the start point

Step 3: Write the correct answer

Distance between the markers = 50 m

  

Part (b)

Step 1: Identify the part of the graph that represents the velocity

• • The graph shows displacement against time
  • Velocity is equal to:

• • Therefore, the slope of the displacement-time graph gives velocity
  • Displacement × time (area under the graph) is not a physical quantity

Step 2: Identify the steepest section of the graph

• • Select the section on the graph where the slope is the steepest
    • This represents the fastest velocity
  • Clearly mark two points on this line which are as far apart as possible 

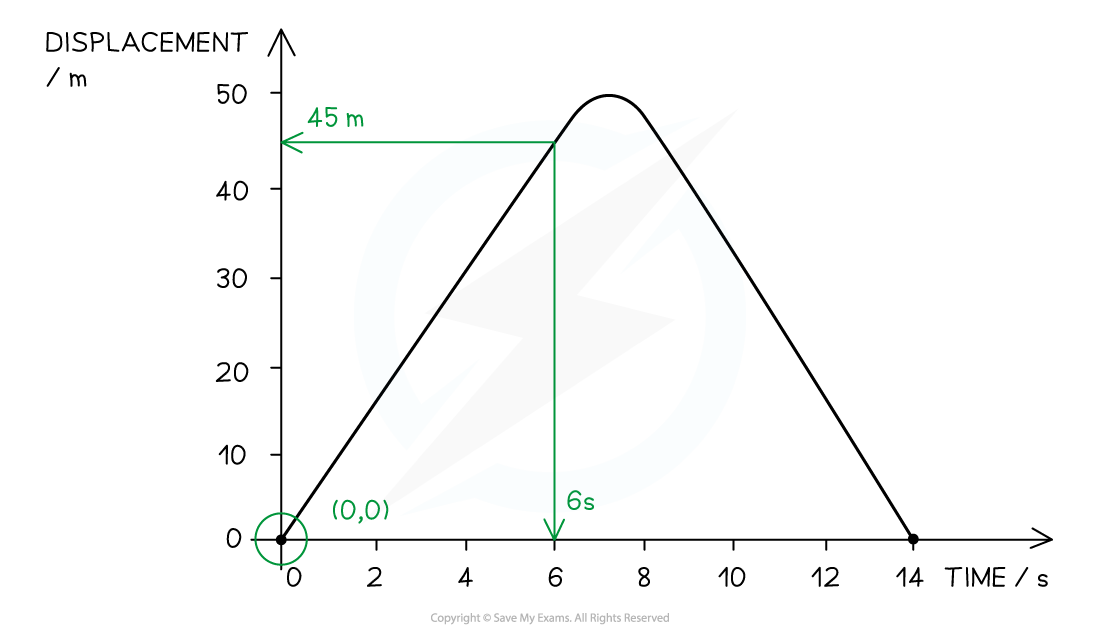
Step 3: Use the coordinates from the graph to calculate the slope

slope = = 7.5 m s⁻¹

Step 4: Write down the answer to the correct number of significant figures

The sprinter's fastest speed = 7.5 m s⁻¹

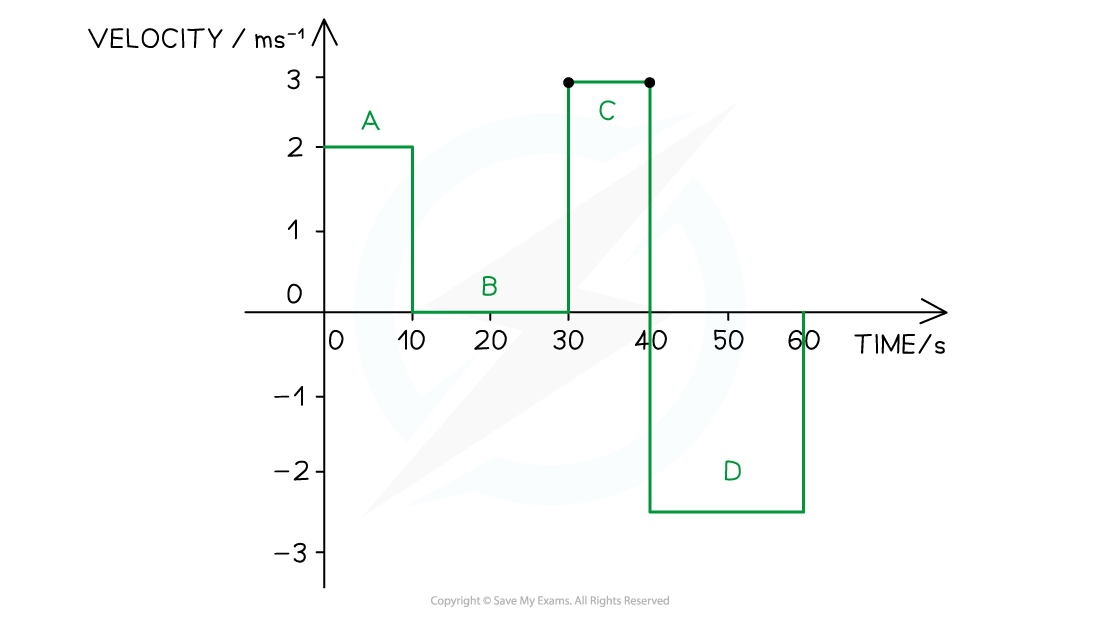
Step 1: Calculate each stage:

Part A

Step 1: Determine the time interval

Time from 0 - 10 s

Step 2: Calculate the velocity by finding the gradient

Gradient =  =  = 2 m s⁻¹

Part B

Step 1: Determine the time interval

Time from 10 - 30 s

Step 2: Calculate the velocity by finding the gradient

Gradient = 0 (horizontal line), velocity = 0 m s⁻¹

Part C

Step 1: Determine the time interval

Time from 30 - 40 s

Step 2: Calculate the velocity by finding the gradient

Gradient =  =  = 3 m s⁻¹

Part D

Step 1: Determine the time interval

Time from 40 - 60 s

Step 2: Calculate the velocity by finding the gradient

Gradient =  =  = − 2.5 m s⁻¹

Step 2: Use the calculated values to sketch a graph