Viscous Drag (Edexcel International AS Physics)

Viscous Drag

• Viscous drag is defined as

the frictional force between an object and a fluid which opposes the motion between the object and the fluid

• Viscous drag is calculated using Stoke’s Law;

F = 6πηrv

• Where
  • F = viscous drag (N)
  • η = coefficient of viscosity of the fluid (N s m⁻² or Pa s)
  • r = radius of the object (m)
  • v = velocity of the object (ms⁻¹)

• The viscosity of a fluid can be thought of as its thickness, or how much it resists flowing
  • Fluids with low viscosity are easy to pour, while those with high viscosity are difficult to pour

• The coefficient of viscosity is a property of the fluid (at a given temperature) that indicates how much it will resist flow
  • The rate of flow of a fluid is inversely proportional to the coefficient of viscosity

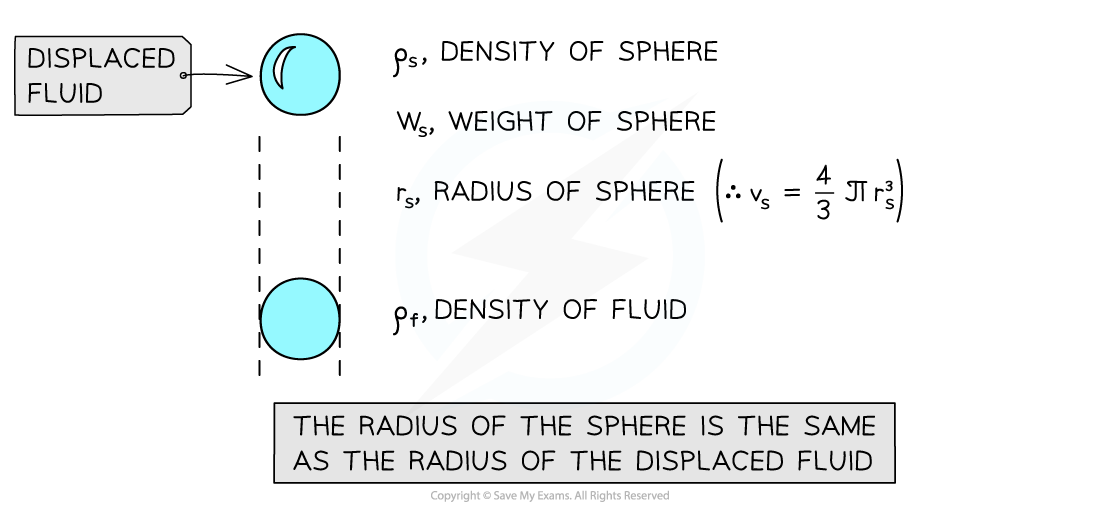
Drag Force at Terminal Velocity

• Terminal velocity is useful when working with Stoke’s Law since at terminal velocity the forces in each direction are balanced

W_s = F_d + U (equation 1)

• Where;
  • W_s = weight of the sphere
  • F_d = the drag force (N)
  • U = upthrust (N)

At terminal velocity forces are balanced: W (downwards) = Fd + U (upwards)

• The weight of the sphere is found using volume, density and gravitational force

W_s =v_sρ_sg

(equation 2)

• Where
  • v_s = volume of the sphere (m³)
  • ρ_s = density of the sphere (kg m^–3)
  • g = gravitational force (N kg⁻¹)

• Recall Stoke’s Law

F_d = 6πηrv_term (equation 3)

• Upthrust equals weight of the displaced fluid
  • The volume of displaced fluid is the same as the volume of the sphere
  • The weight of the fluid is found from volume, density and gravitational force as above

(equation 4)

• Substitute equations 2, 3 and 4 into equation 1

• Rearrange to make terminal velocity the subject of the equation

• Finally, cancel out r from the top and bottom to find an expression for terminal velocity in terms of the radius of the sphere and the coefficient of viscosity

 

• This final equation shows that terminal velocity is;
  • directly proportional to the square of the radius of the sphere
  • inversely proportional to the viscosity of the fluid

Conditions for Stoke’s Law Equation

• The equation can only be used when certain conditions are met;
  • The flow is laminar
  • The object is small
  • The object is spherical
  • Motion between the sphere and the fluid is at a slow speed

 

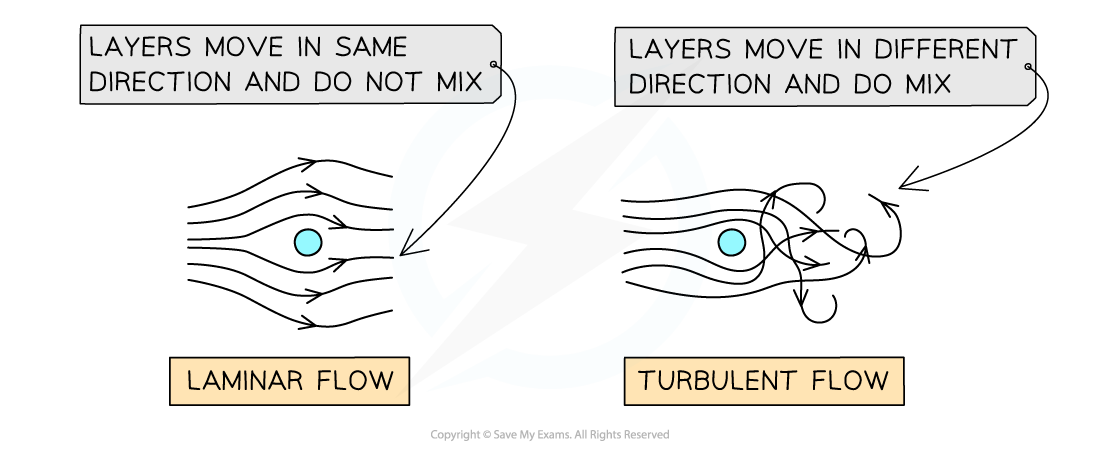
Laminar and Turbulent Flow

• As an object moves through a fluid, or a fluid moves around an object, layers in the fluid are created
• In laminar flow all the layers are moving in the same direction and they do not mix
• This tends to happen for slow moving objects, or slow flowing liquids
• The equation above only applies for laminar flow
• In turbulent flow the layers move in different directions and the layers do mix

Changing Viscosity

• Viscosity is temperature-dependent
  • Liquids are less viscous as temperature increases
  • Gases get more viscous as temperature increases

Step 1: List the known quantities in SI units

• • Radius of the sphere, r_s = 5.0 mm = 5.0 × 10^-3 m
  • Terminal velocity of the sphere, v = 0.03 m s^-1
  • Viscosity of oil, η = 0.3 Pa s
  • Density of oil, ρ_f = 900 kg m⁻³

Step 2: Sketch a free-body diagram to resolve the forces at constant speed

W_s = F_d + U

Step 3: Calculate the value for viscous drag, F_d

F_d = 6πηrv = 6 × π × 0.3 × 5.0 × 10^-3 × 0.03 = 0.008482

Step 4: Write the complete answer to the correct significant figures and include units

• •  The viscous drag, F_d  = 8.5 × 10^-4 N