Discrete Probability Distributions | Edexcel International AS Maths: Statistics 1 Revision Notes 2019

Did this video help you?

Discrete Random Variables

What is a discrete random variable?

A random variable is a variable whose value depends on the outcome of a random event
- The value of the random variable is not known until the event is carried out (this is what is meant by 'random' in this case)
Random variables are denoted using upper case letters (X , Y , etc )
Particular outcomes of the event are denoted using lower case letters ( x, y, etc)
$P (X = x)$ means "the probability of the random variable X taking the value $x$ "
A discrete random variable (often abbreviated to DRV) can only take certain values within a set
- Discrete random variables usually count something
- Discrete random variables usually can only take a finite number of values but it is possible that it can take an infinite number of values (see the examples below)
Examples of discrete random variables include:
- The number of times a coin lands on heads when flipped 20 times
  (this has a finite number of outcomes: 0,1,2,…,20)
- The number of emails a manager receives within an hour
  (this has an infinite number of outcomes: 1,2,3,…)
- The number of times a dice is rolled until it lands on a 6
  (this has an infinite number of outcomes: 1,2,3,…)
- The number on a bingo ball when one is drawn at random
  (this has a finite number of outcomes: 1,2,3…,90)

Did this video help you?

Probability Distributions (Discrete)

What is a probability distribution?

A discrete probability distribution fully describes all the values that a discrete random variable can take along with their associated probabilities
- This can be given in a table (similar to GCSE)
- Or it can be given as a function (called a probability mass function)
- They can be represented by vertical line graphs (the possible values for along the horizontal axis and the probability on the vertical axis)
The sum of the probabilities of all the values of a discrete random variable is 1
- This is usually written $ΣP (X = x) = 1$
A discrete uniform distribution is one where the random variable takes a finite number of values each with an equal probability
- If there are n values then the probability of each one is $\frac{1}{n}$

4-1-1-discrete-probability-distributions-diagram-1

Did this video help you?

Cumulative Probabilities (Discrete)

How do I calculate probabilities using a discrete probability distribution?

For probability distributions that take a small number of values start by drawing a table to represent the probability distribution
- If the distribution is given as a function then find each probability
- If any probabilities are unknown then use algebra to represent them
  - Form an equation using $\sum P (X = x) = 1$
To find $P (X = k)$
- If k is a possible value of the random variable X then $P (X = k)$ will be given in the table
- If $k$ is not a possible value then $P (X = k) = 0$

What is the cumulative distribution function?

The cumulative distribution function, denoted $F(x)$ , is the probability that the random variable takes a value less than or equal to x.
- $F (x) = P (X \leq x)$
You may be asked to draw a table for the cumulative distribution function
- This will be similar to a probability distribution function but instead the bottom row will be F(x) instead of P(X = x)

How do I calculate cumulative probabilities?

To find $P (X \leq x)$ (equivalently F(x))
- Identify all possible values, $x_{i}$ , that X can take which satisfy $x_{i} \leq k$
- Add together all their corresponding probabilities
- $P (X \leq k) = \sum_{x_{i} \leq k} P (X = x_{i})$
Using a similar method you can find $P (X < k), P (X \geq k)$ and $P (X > k)$
As all the probabilities add up to 1 you can form the following equivalent equations:
- $P (X < k) + P (X = k) + P (X > k) = 1$
- $P (X > k) = 1 - P (X \leq k)$
- $P (X \geq k) = 1 - P (X < k)$
To calculate more complicated probabilities such as $P (X^{2} < 4)$
- Identify which values of the random variable satisfy the inequality or event in the brackets
- Add together the corresponding probabilities

How do I know which inequality to use?

$P (X \leq k)$ would be used for phrases such as:
- At most k, no greater than k, etc
$P (X < k)$ would be used for phrases such as:
- Fewer than k
$P (X \geq k)$ would be used for phrases such as:
- At least k , no fewer than k, etc
$P (X > k)$ would be used for phrases such as:
- Greater than k, etc

Worked example

The probability distribution of the discrete random variable $X$ is given by the function

$P (X = x) = \{\begin{cases} k x^{2} & x = - 3, - 1, 2, 4 \\ 0 & otherwise \end{cases}$

(a)

Show that

k = \frac{1}{30} .

(b)

Calculate

F (3)

(c)

Calculate

P (X^{2} < 5)

(a) Show that

k = \frac{1}{30}

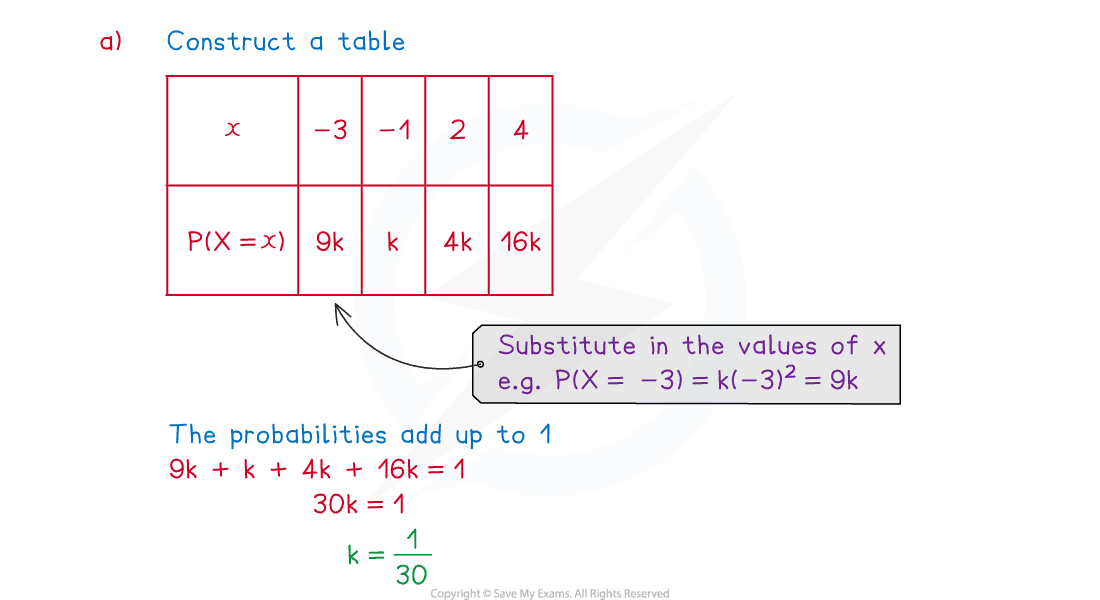
3-1-1-discrete-probability-distributions-we-solution-part-1

(b)

Calculate

F (3)

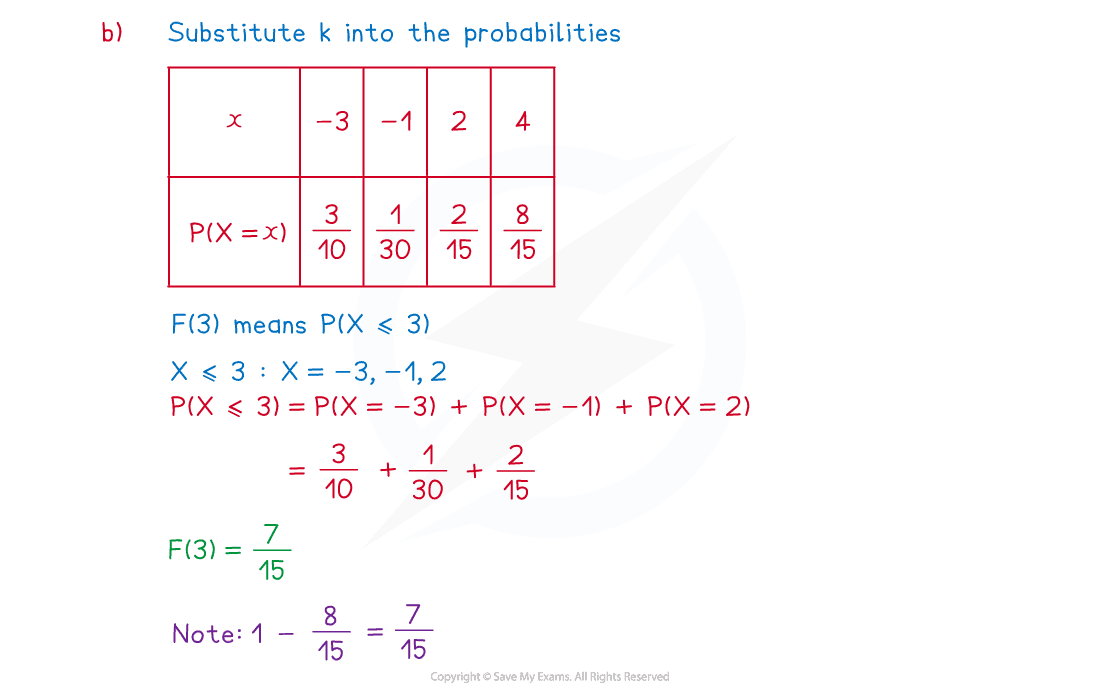
3-1-1-discrete-probability-distributions-we-solution-part-2

(c)

Calculate

P (X^{2} < 5)

3-1-1-discrete-probability-distributions-we-solution-part-3

Examiner Tip

Try to draw a table if there are a finite number of values that the discrete random variable can take
When finding a probability, it will sometimes be quicker to subtract the probabilities of the unwanted values from 1 rather than adding together the probabilities of the wanted values
Always make sure that the probabilities are between 0 and 1, and that they add up to 1!

Discrete Probability Distributions (Edexcel International AS Maths: Statistics 1)

Revision Note

Discrete Random Variables

What is a discrete random variable?

Probability Distributions (Discrete)

What is a probability distribution?

Cumulative Probabilities (Discrete)

How do I calculate probabilities using a discrete probability distribution?

What is the cumulative distribution function?

How do I calculate cumulative probabilities?

How do I know which inequality to use?

Worked example

Examiner Tip

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Dan