Definition of Derivatives

What is the derivative of a function?

Differentiation is an operation that calculates the rate of change of a function with respect to a variable
- This means how much the function varies when the variable increases by one unit
To differentiate a function (f(x)) with respect to the variable x we use the notation
- $\frac{d}{d x} (f (x))$
The result is called the derivative

What is the link between derivatives and gradients?

The rate of change of a function f(x) with respect to x can be thought of as the gradient function of the graph y = f(x)
- We can write the gradient function (or derivative) as
  - $f' (x)$ or $\frac{d y}{d x}$
The rate of change of a function (or the gradient of its graph) varies for different values of x
- For a linear function f(x) = mx + c the gradient is constant
  - We can write this as $f' (x) = m$ or $\frac{d y}{d x} = m$
- For the quadratic function f(x) = x² the gradient varies
  - Near the origin the gradient is close to 0
  - As x increases the gradient of the graph increases

How can I find the derivative of a function at a point?

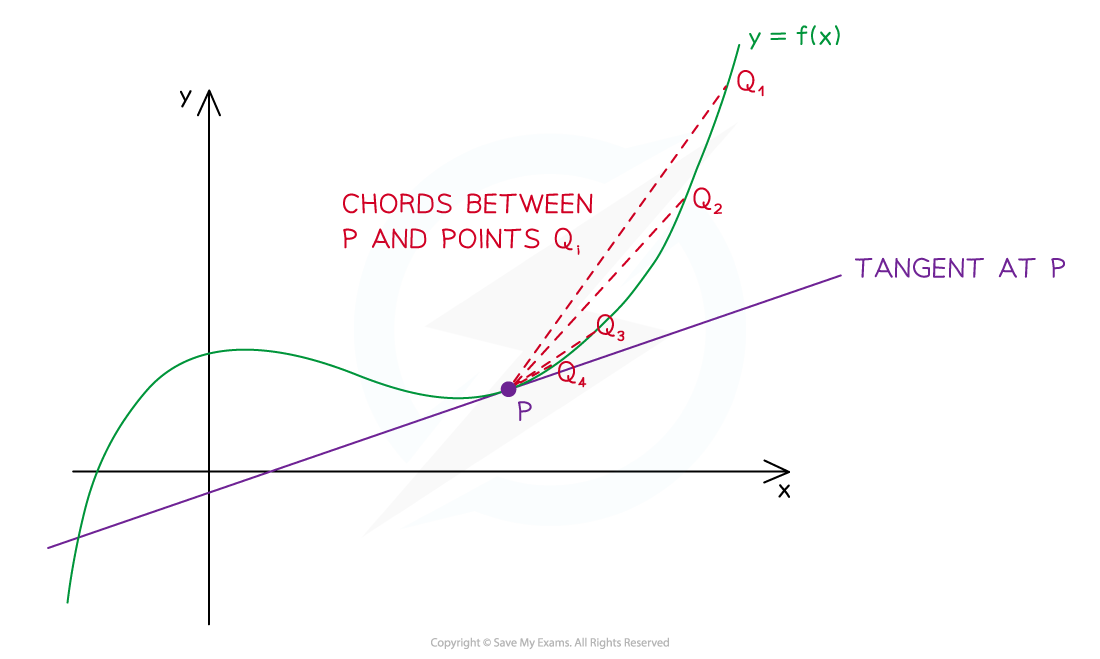
The derivative of a function (or gradient of its graph) at a point is equal to the gradient of the tangent to the graph at that point
To estimate the gradient you could draw the tangent and calculate its gradient
To find the actual gradient at a point x
- Pick a second point on the curve close to the first point (call it x + h)
- Calculate the gradient of the chord joining the two points
  - $\frac{f (x + h) - f (x)}{(x + h) - x} = \frac{f (x + h) - f (x)}{h}$
- Move the second point closer to the first point (make h get close to zero)
- Examine what happens to the gradient of the chord
- The gradient of the tangent will be the limit of the gradients of the chords
  - $f^{'} (x) = \lim_{h \to 0} \frac{f (x + h) - f (x)}{h}$
  - You do not need to remember this formula

5-1-2-definiton-of-derivatives-diagram-1

Worked example

fd_jCRti_5-1-2-definiton-of-derivatives-we-solution-part-1

OwgQJzIG_5-1-2-definiton-of-derivatives-we-solution-part-2

Examiner Tip

Deriving a derivative from scratch is not examinable
This revision note is intended to give you an understanding of what derivatives do

Definition of Derivatives (Edexcel International AS Maths: Pure 1)

Revision Note

What is the derivative of a function?

What is the link between derivatives and gradients?

How can I find the derivative of a function at a point?

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

1. Algebra & Functions

1.1 Laws of Indices & Surds

1.1.1 Laws of Indices

1.1.2 Manipulating Surds

1.1.3 Surds - Rationalising the Denominator

1.2 Quadratics

1.2.1 Quadratic Graphs

1.2.2 Discriminants

1.2.3 Completing the square

1.2.4 Solving Quadratic Equations

1.2.5 Further Solving Quadratic Equations (Hidden Quadratics)

1.3 Simultaneous Equations

1.3.1 Linear Simultaneous Equations - Elimination

1.3.2 Linear Simultaneous Equations - Substitution

1.3.3 Quadratic Simultaneous Equations

1.4 Inequalities

1.4.1 Linear Inequalities

1.4.2 Quadratic Inequalities

1.4.3 Inequalities on Graphs

1.5 Polynomials

1.5.1 Expanding Brackets

1.5.2 Factorising Expressions

1.6 Graphs of Functions

1.6.1 Sketching Polynomials

1.6.2 Reciprocal Graphs - Sketching

1.6.3 Solving Equations Graphically

1.6.4 Proportional Relationships

1.6.5 Modelling with Functions

1.7 Transformations of Functions

1.7.1 Translations

1.7.2 Stretches

1.7.3 Reflections

2. Coordinate Geometry

2.1 Equation of a Straight Line

2.1.1 Basic Coordinate Geometry

2.1.2 Parallel & Perpendicular Gradients

2.1.3 Equation of a Straight Line

2.1.4 Modelling with Straight Lines

3. Trigonometry

3.1 Basic Trigonometry

3.1.1 Trigonometry - Definitions

3.1.2 Right-Angled Triangles

3.1.3 Non-Right-Angled Triangles

3.2 Radian Measure

3.2.1 Radian Measure

3.2.2 Trigonometry Exact Values

3.3 Trigonometric Functions

3.3.1 Graphs of Trigonometric Functions

3.3.2 Transformations of Trigonometric Functions

4. Differentiation

4.1 Differentiation

4.1.1 Definition of Gradient

4.1.2 Definition of Derivatives

4.1.3 Differentiating Powers of x

4.1.4 Gradients, Tangents & Normals

4.1.5 Second Order Derivatives

5. Integration

5.1 Integration

5.1.1 Fundamental Theorem of Calculus

5.1.2 Integrating Powers of x

Author: Dan