Rationalising the Denominator with Surds (Edexcel International AS Maths): Revision Note
Exam code: XMA01
Did this video help you?
Rationalising the denominator with surds
How do I rationalise the denominator?
Rationalising a denominator changes a fraction with surds in its denominator, into an equivalent fraction where the denominator is a rational number (usually an integer) and any surds are in the numerator
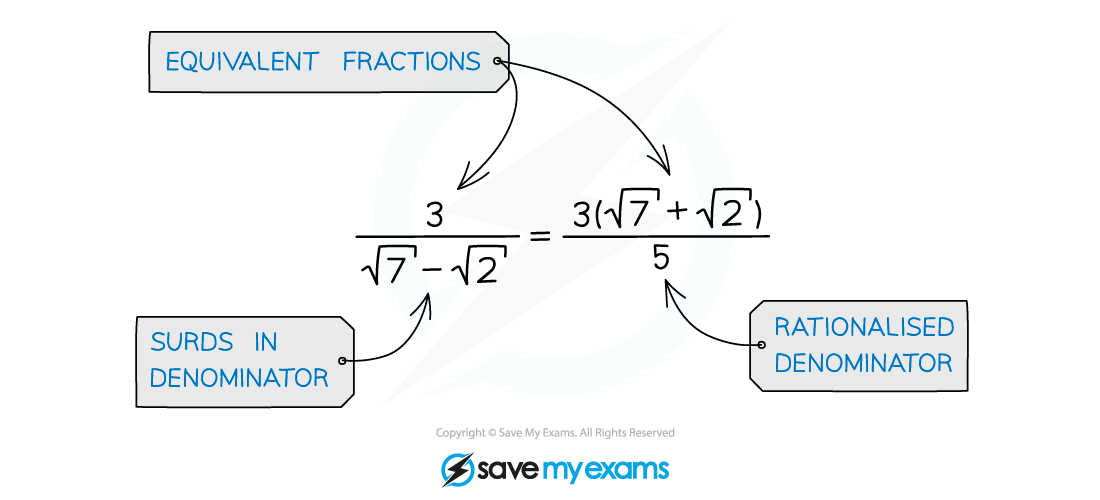
There are three cases you need to know how to deal with when rationalising denominators:

Examiner Tips and Tricks
If an exam question asks you to give an answer, for example, "in the form p + q√3 , where p and q are rational numbers", this does NOT mean that p and q have to be integers, or positive!
Remember: both integers and fractions (both positive and negative) are rational numbers
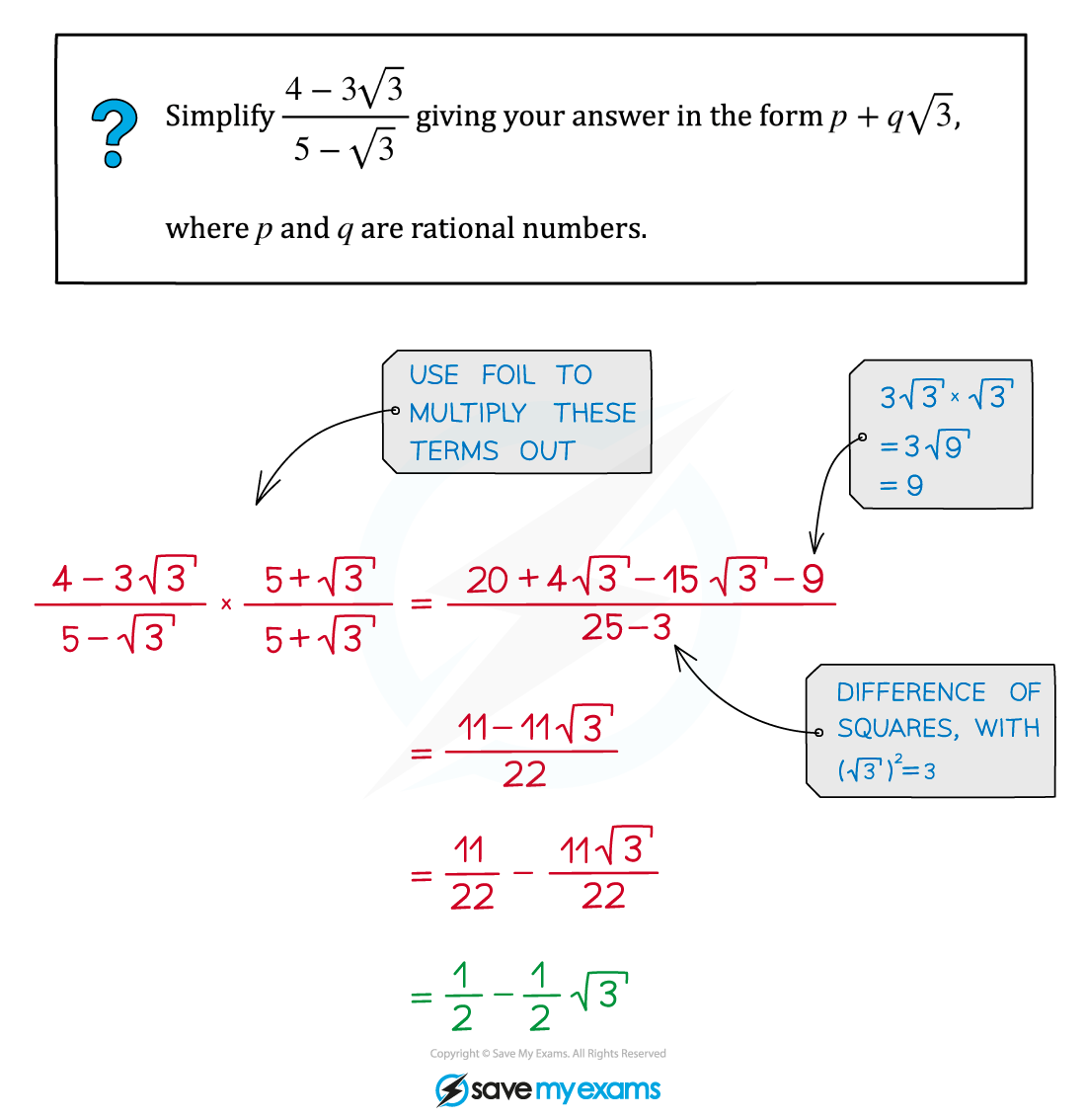
Worked Example

Unlock more, it's free!
Did this page help you?