Forces in 2D (Vector Notation) (Edexcel International AS Maths): Revision Note
Exam code: XMA01
Did this video help you?
Forces in 2D - Vector Notation
How are forces and vectors linked?
Forces are vectors – they have magnitude and direction.
The magnitude of a force is measured in Newtons and the direction of a force is an angle, usually measured in degrees, anti-clockwise from the horizontal
There are other ways to talk about direction – in particular Cartesian coordinates(x, y) are used to describe the position of a point in two-dimensional space (plane), relative to a fixed origin O.
You may see questions start with a sentence along the lines of “Relative to the frame of reference Oxy …” – this means the two-dimensional space (plane) and distances within it will be based on horizontal (x) and vertical (y) components relative to the origin O.
What is vector notation?
Forces in 2D should be given in the form pi +qj where i and j are unit vectors
Both column vectors and i, j notation can be used for calculating resultant vectors
Column vectors can be useful when calculating with vectors as mistakes are less common, but you must remember to change the answer back to i, j notation form
A force written as a vector is written with its two components separated so the magnitude and direction of the vector are not directly known
What are the notations for magnitude and direction?
The magnitude of the force F N would be denoted by |F| N or F N – notice the use of bold and italics in particular
Direction is an angle, usually measured in degrees anti-clockwise from the horizontal, θ° is usually used
How do I find the magnitude and direction of a force from its components?
For a force F = xi + yj N to find
its magnitude, |F| N or F N, use Pythagoras’ theorem
its direction (as an angle), use a diagram and trigonometry

If either (or both) components are negative then still use a diagram and
but
treat x and y as positive (so |x| and |y| strictly speaking)
the angle found from
may need adjusting depending on where, and which way, the direction is being measured from
e.g. Find the direction at which the force F = (-8i - 6j) N, giving your answer as an angle measured in degrees anti-clockwise from the positive horizontal direction

What does equilibrium with vectors mean?
In two dimensions a particle is in equilibrium if the resultant force acting on it in both directions is zero
For vectors in i-j notation, a resultant force of zero would look like (0i + 0j) N
Both forms may be written as 0 N (called ‘the zero vector’)
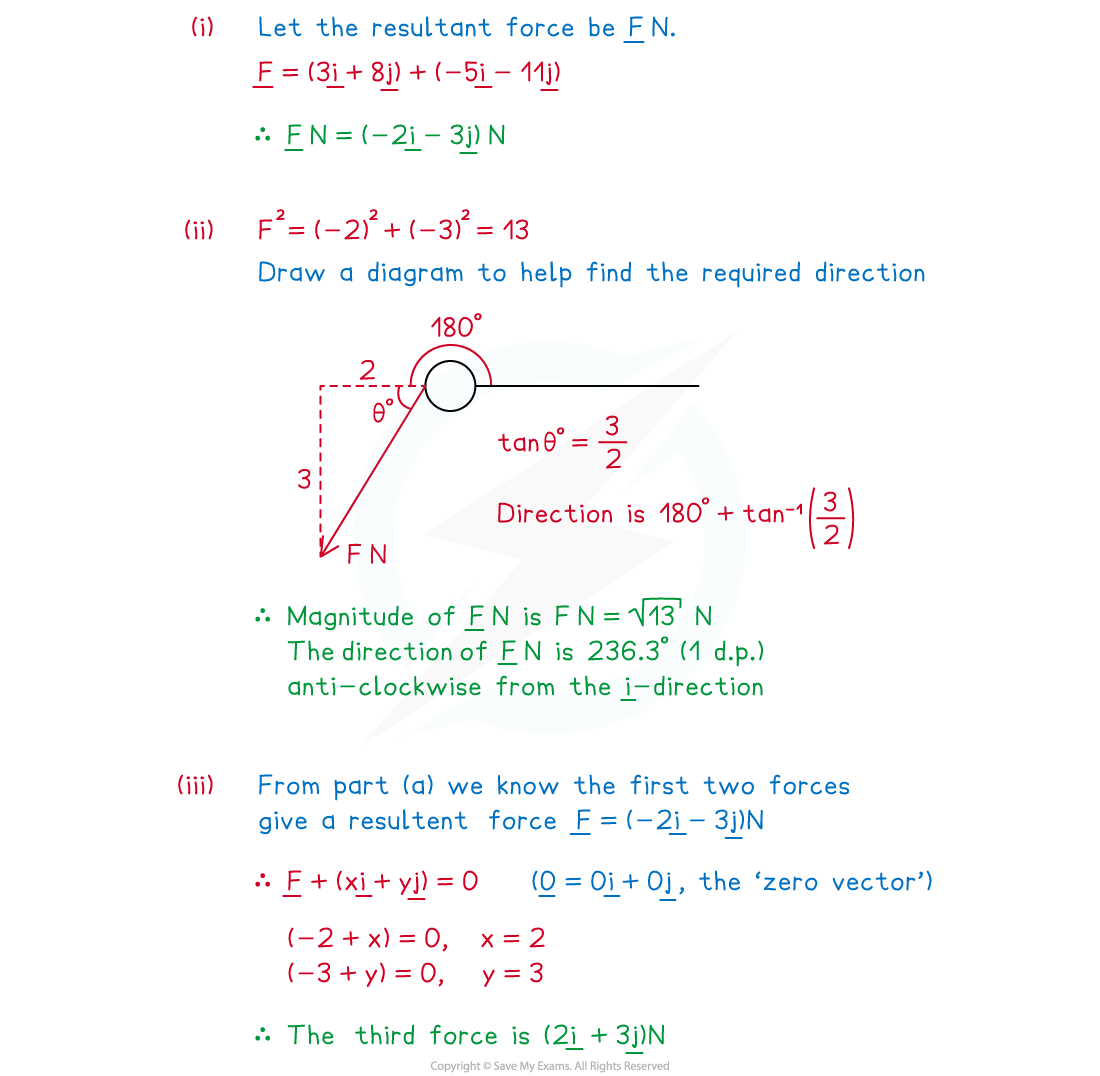
Worked Example
Two forces, (3i + 8j) N and (—5i — llj) N act on a particle.
(i) Find the resultant force.
(ii) Find the magnitude of the resultant force and its direction as an angle measured anti-clockwise from the i-direction.
(iii) A third force is applied to the particle such that it is brought into equilibrium. Find the third force, giving your answer in the form
Answer:
Examiner Tips and Tricks
Ideally you should stick to the i-,j- vector notation used in a question but if you prefer to use column vectors within calculations you can use a mixture within the same question. Just be careful your final answer is in the correct format.
Draw diagrams – including ‘mini’-diagrams of individual forces/vectors – this can help in understanding a problem and being accurate.

Unlock more, it's free!
Did this page help you?