International ASMaths: Decision 1EdexcelRevision NotesAlgorithms on GraphsThe Route Inspection AlgorithmRoute Inspection

Route Inspection (Edexcel International AS Maths: Decision 1)

Revision Note

Naomi C

Author

Naomi C

Last updated

The Chinese Postman Problem

What is the Chinese postman problem?

  • The route inspection problem is also known as the Chinese postman problem
  • You are required to find the route of least weight that traverses every edge in a graph
    • The route must start and finish at the same vertex
  • Some edges may need to be traversed more than once
    • The challenge is to minimise the total weight of these repeated edges
  • Variations to the route inspection problem could involve
    • The start and finish vertices being different
    • Certain edges being disregarded
      • E.g. a road closure
    • Repetition being required on the route
      • E.g. a road sweeper covering both sides of the road

Networks with 0 or 2 Odd Vertices

How do I solve the Chinese postman problem in networks with 0 or 2 Odd Vertices?

  • If the graph is Eulerian
    • All of the vertices in the graph are even
      • I.e. there are 0 odd nodes
    • It will be possible to find an Eulerian circuit
      • I.e. a route that traverses each edge exactly once, starting and finishing at the same vertex
    • No route or edges will need repetition 
    • The shortest route will be the sum of the weights of the edges in the network
  • If the graph is semi-Eulerian
    • There will be one pair of odd vertices
      • I.e. there will be 2 odd nodes
    • If the route has to start and end at the same vertex
      • The shortest path between the two odd nodes will need to be found
        • The edges making that shortest path will need to be repeated
      • The shortest route will be the sum of the weights of the edges in the network plus the weight of the repeated edges
    • If the route starts at one of the odd vertices and ends at the other
      • No path/edges will need repetition
      • The shortest route will be the sum of the weights of the edges in the network

What are the steps of the Chinese postman algorithm?

  • STEP 1
    Inspect the degree of all of the vertices and identify any odd nodes
     
  • STEP 2
    If all of the vertices are even go to STEP 3
    If there is one pair of odd nodes, find the shortest path between them
    The edges making this path will need to be repeated so add them to the graph
    (Once they are added to the graph every node will be even, so an Eulerian circuit will exist)
      
  • STEP 3
    Write down an Eulerian circuit of the adjusted graph to find a possible route
    • Find the sum of the edges traversed to find the total weight

Examiner Tip

  • Look carefully for the shortest path when connecting two odd vertices
    • A path made up of several edges will sometimes be a shorter distance than a more direct route

Worked example

The network shown below displays the distance, in metres, of the cables in a network between different connection points A, B, C, D, E and F.

Each length of cable must be inspected.

jv2R5V-u_chinese-postman
 

a)
Find the shortest route that allows all the cables to be inspected, and that starts and finishes at connection point E.

  • STEP 1
    Inspect the order of the nodes
     
A: 5 (odd)
B: 2 (even)
C: 3 (odd)
D: 2 (even)
E: 4 (even)
F: 2 (even)

  • STEP 2
    There is exactly one pair of odd vertices, A and C
    The shortest path between A and C is ABC so the edges AB and BC need to be repeated
    An Eulerian circuit, starting and ending at connection point E, is now possible
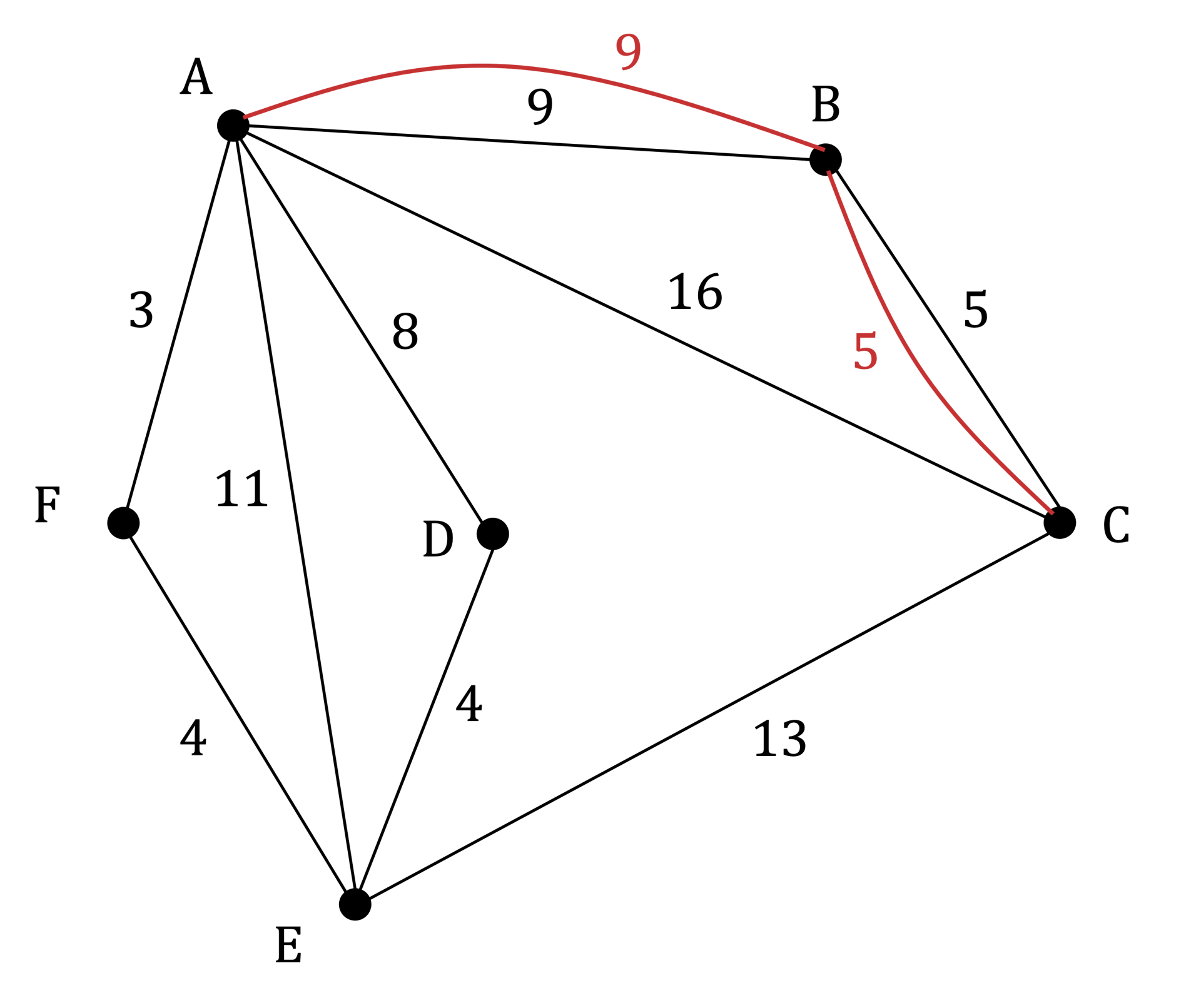
     chinese-postman-2
  • STEP 3
    Find an Eulerian circuit, starting and ending at connection point E
Shortest route: EFAEDABACBCE

b)
State the total length of the shortest route.
 
Add together the lengths of the edges in the original graph
 
3 + 4 + 4 + 5 + 8 + 9 + 11 + 13 + 16 = 73
 
Add the result to the lengths of the repeated edges
 
73 + 5 + 9 = 87
 
Shortest route = 87 m

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Did this page help you?

    Previous:Dijkstra's AlgorithmNext:Route Inspection & Repeated Routes
    Naomi C

    Author: Naomi C

    Expertise: Maths

    Naomi graduated from Durham University in 2007 with a Masters degree in Civil Engineering. She has taught Mathematics in the UK, Malaysia and Switzerland covering GCSE, IGCSE, A-Level and IB. She particularly enjoys applying Mathematics to real life and endeavours to bring creativity to the content she creates.