Roots in Intervals (Edexcel International AS Further Maths)

Revision Note

Written by: Mark Curtis

Reviewed by: Dan Finlay

Roots in Intervals

What is a root of an equation?

A root of the equation $f (x) = 0$ is a solution
- If $x = α$ is a root of $f (x) = 0$ then $f (α) = 0$
  - The Greek letter alpha is often used
To find $α$ exactly, you need to solve the equation algebraically (analytically)
Some equations cannot be solved algebraically
- In which case you can approximate a root to a given accuracy
  - For example, to 3 decimal places
- This is called solving equations numerically

What is an interval?

If you don't know the root but know that it lies between $x = a$ and $x = b$ , where $a < b$ , then
- $a < x < b$ is an interval containing the root
Intervals can be written using bracket notation
- $(a, b)$ is $a < x < b$
- $[a, b]$ is $a \leq x \leq b$

How do I show that an interval contains a root?

Use the sign-change and continuity test to show that the interval $a < x < b$ contains a root to the equation $f (x) = 0$
Show that $f (a)$ and $f (b)$ have different signs and check that $f (x)$ is continuous across $a < x < b$
- Then the interval $a < x < b$ must contains a root
- Continuous means no jumps or asymptotes in the interval
  - Check the equation does not divide by zero within the interval
  - (Jumps or asymptotes outside of the interval are fine)
- You must write a conclusion to the test in words, for example:
  - " $f (x)$ has a sign change in the interval $a < x < b$ and $f (x)$ is continuous in the interval, so a root must lie in the interval $a < x < b$ "

Examiner Tips and Tricks

When writing your conclusion in the exam, don't forget to mention $f (x)$ being continuous in the interval!

How do I show that an equation has a root to a given accuracy?

If asked to show that $x = 1.39$ is the root of an equation to 2 decimal places
- write an interval using the lower and upper bound of the root
  - $1.385 < x < 1.395$
- use the sign-change and continuity test on this interval

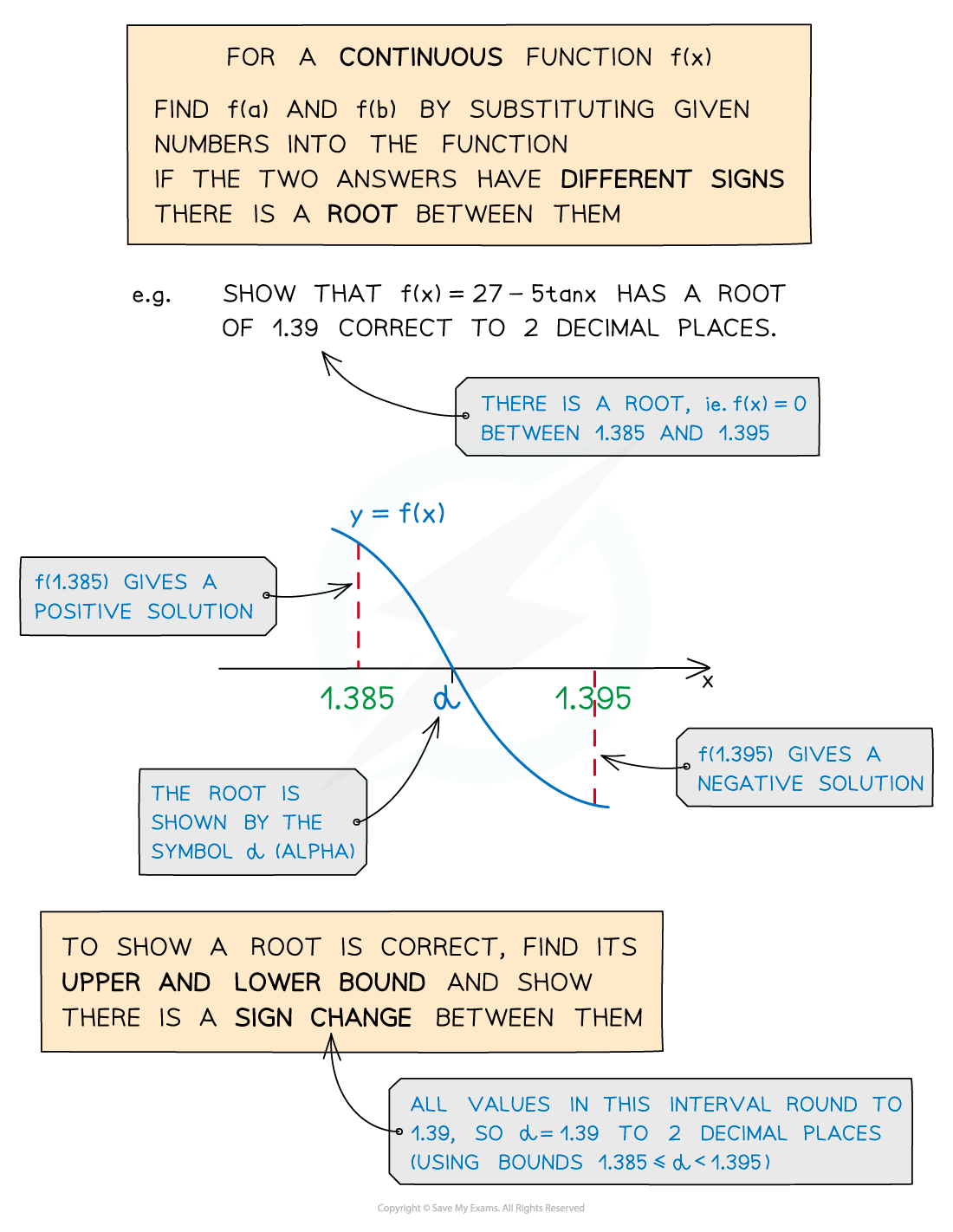
How to use the sign change test to show that a root is true to a given accuracy

A suitable conclusion would be
- $f (x)$ has a sign change in the interval $1.385 < x < 1.395$
- and $f (x)$ is continuous in the interval
- so a root must lie in the interval $1.385 < x < 1.395$
- All values in the interval round to $1.39$
- so the root is $1.39$ to 2 decimal places

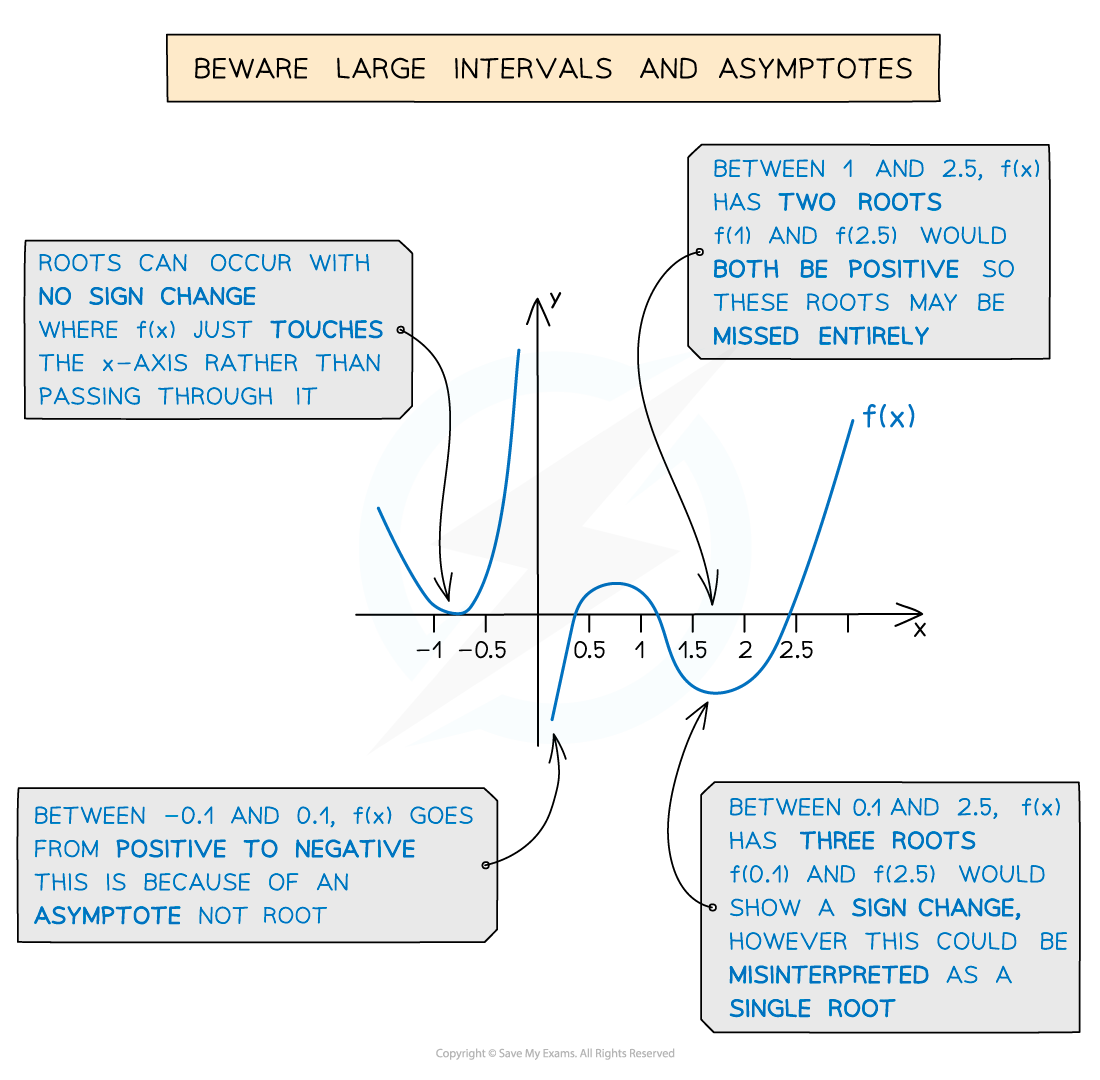
How do I know when the sign-change test fails?

You need to know the three cases when the sign-change and continuity test fails to work properly:
- If the curve $y = f (x)$ only touches the $x$ -axis at the root, you will not see a sign change (even though there is a root)
- If the curve $y = f (x)$ has an asymptote in the interval, then you may see a sign change (but there is no root)
  - The asymptote means $f (x)$ is not continuous
- If the interval is too large, there may be more than one root in it
  - You may see a sign change (an odd number of roots)
  - Or you may not see a sign change (an even number of roots)

A diagram showing the cases when the change of sign test fails

Worked Example

The equation $f (x) = 0$ where $f (x) = x - x^{4} + \frac{1}{2 x - 1}$ has exactly one positive root.

(a) Show that the intervals $[0, 1]$ and $[1, 2]$ both have a change of sign in $f (x)$ .

Substitute $x = 0$ , $x = 1$ and $x = 2$ into $f (x)$

$\begin{array}{rcl} f (0) & = & 0 - 0^{4} + \frac{1}{2 \times 0 - 1} = - 1 \\ f (1) & = & 1 - 1^{4} + \frac{1}{2 \times 1 - 1} = 1 \\ f (2) & = & 2 - 2^{4} + \frac{1}{2 \times 2 - 1} = - \frac{41}{3} \end{array}$

Comment that the signs are different for each interval

$f (0) = - 1 < 0$ and $f (1) = 1 > 0$ so there is a sign change in $[0, 1]$
$f (1) = 1 > 0$ and $f (2) = - \frac{41}{3} < 0$ so there is a sign change in $[1, 2]$

(b) Determine, with a reason, which of the intervals contains the root.

An interval contains a root if $f (x)$ has a sign change and is continuous in that interval
Check to see if $f (x)$ is continuous in $[0, 1]$
You need to look for any asymptotes

$\frac{1}{2 x - 1}$ is undefined when $x = \frac{1}{2}$

The asymptote $x = \frac{1}{2}$ lies in the interval $[0, 1]$
There are no other asymptotes and only one root

The interval $[1, 2]$ contains the root as there is a sign change and $f (x)$ is continuous
The interval $[0, 1]$ contains the asymptote $x = \frac{1}{2}$ so $f (x)$ is not continuous

Last updated: 5 April 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Forming Quadratics with New RootsNext:Interval Bisection