Identifying Appropriate Apparatus (Edexcel International A Level (IAL) Physics): Revision Note
Exam code: YPH11
Identifying Appropriate Apparatus
When planning an experiment, the first step is to identify the apparatus required
Each experiment will have its own unique set of apparatus
The apparatus is the equipment needed to carry out the experiment
This includes both what you are measuring and how you are measuring it
Common apparatus include:
Metre rulers - to measure distance and length
Balances - to measure mass
Protractors - to measure angles
Stopwatches - to measure time
Ammeters - to measure current
Voltmeters - to measure potential difference
More complicated instruments such as the micrometer screw gauge and Vernier calipers can be used to more accurately measure length
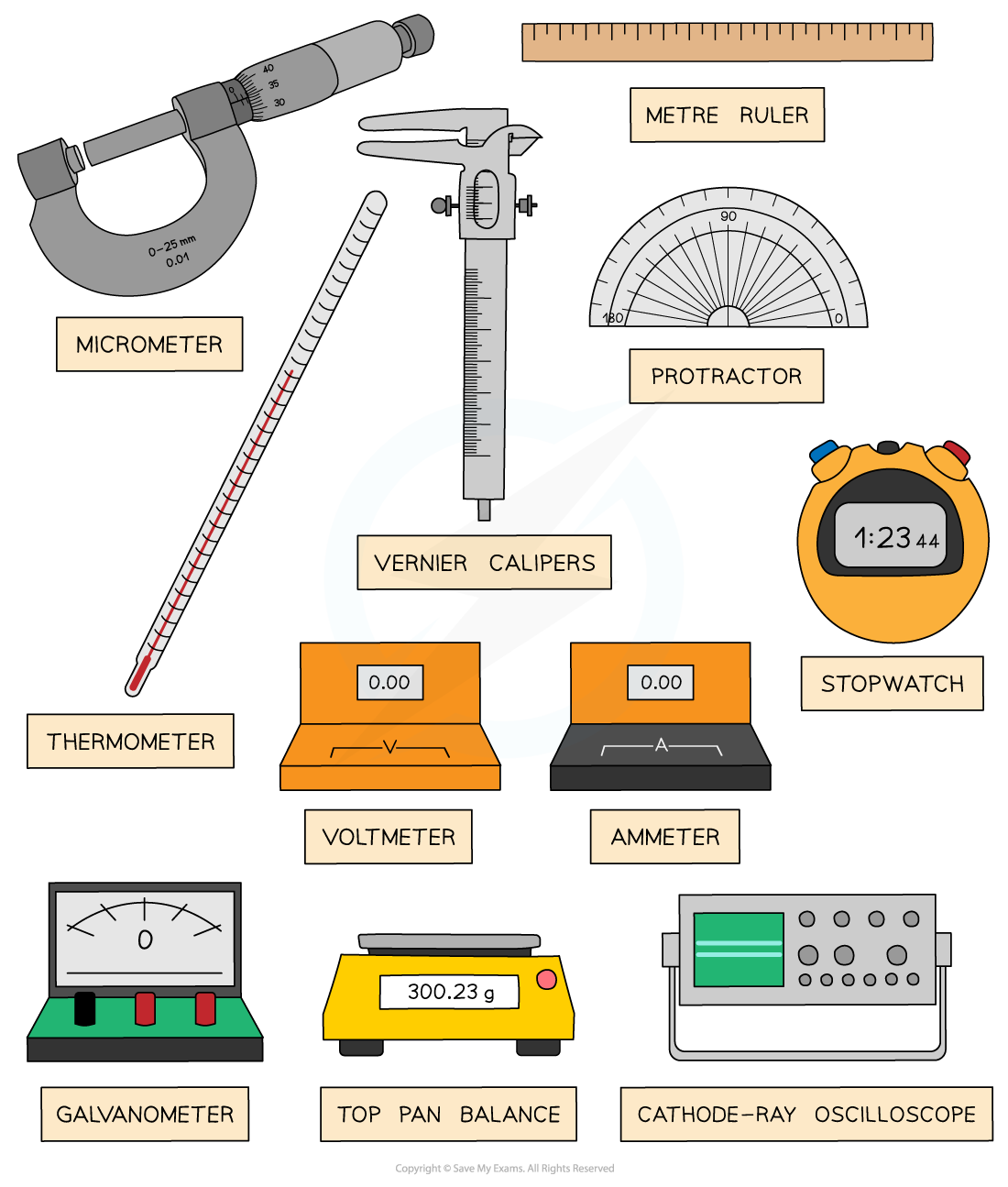
Examples of apparatus used in scientific experiments
The apparatus required depends on what you are trying to measure
A few examples are shown in the table below
Apparatus Table
Quantity | Apparatus |
Length | Metre ruler, Micrometer, Vernier caliper |
Mass | Top–pan balance |
Angle | Protractor |
Time | Stopwatch |
Temperature | Thermometer |
Potential difference | Voltmeter |
Current | Ammeter |
Frequency | Oscilloscope |
An example of apparatus for measuring the specific heat capacity of an aluminium block is shown below:
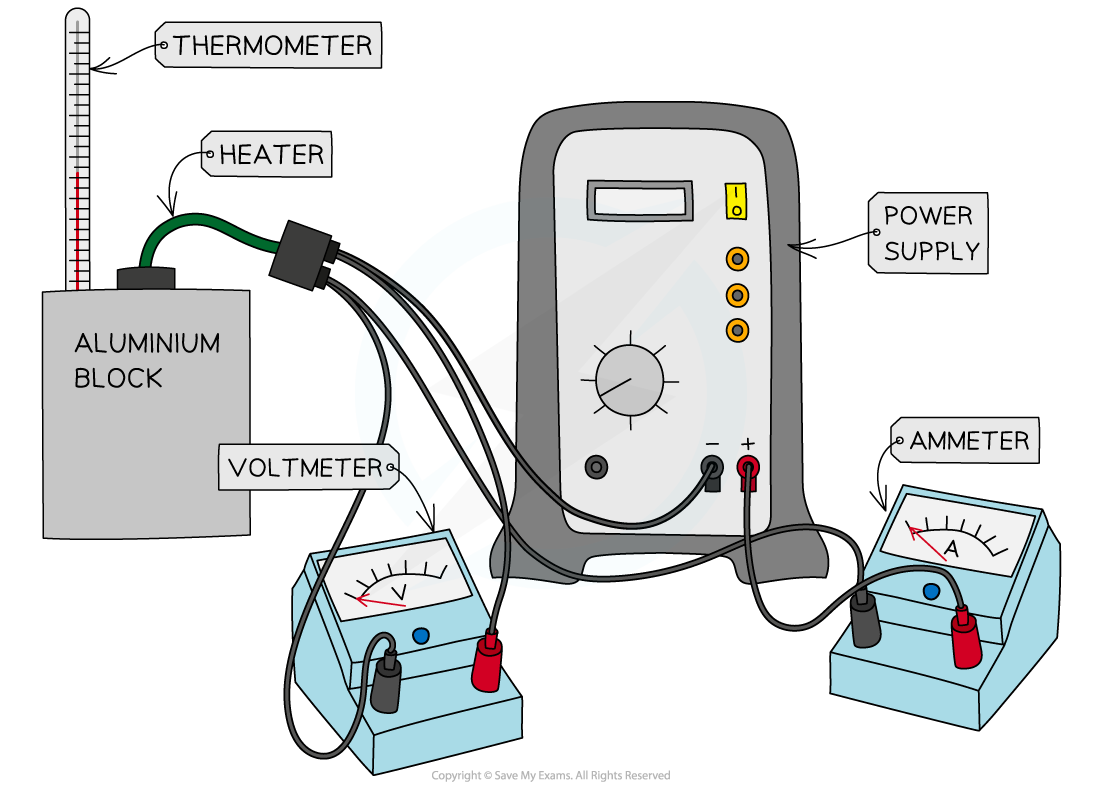
Apparatus needed to measure specific heat capacity
This includes:
A block of the substance (preferably 1kg in mass) or in the case of a fluid, a beaker containing a known mass of the fluid
A thermometer
An appropriate heater (e.g. an immersion heater)
A power source
A joule meter or a voltmeter, ammeter and stop-clock (I will assume we have the latter)
Wires and connectors
Range & Resolution of Instruments
All instruments have a range and resolution
The range is the highest and lowest value an instrument can measure
The resolution is the smallest increment an instrument can measure
Examples of resolutions for instruments are:
Experimental Instrument | Typical Resolution | Typical Range |
Metre ruler | 1 mm | 0 – 1 m |
Vernier Calipers | 0.1 mm | 0 – 300 mm |
Micrometer Screw Gauge | 0.01 mm | 0 – 25 mm |
Top-pan Balance | 0.01 g | 0 – 0.1 g |
Protractor | 1° | 0 – 180° |
Stopwatch | 0.01 s | 0 – 9 hours 59 mins 59.99 seconds |
Thermometer | 1 °C | –10 °C – 110 °C |
Voltmeter | 1 mV – 0.1 V | 0 – 1000 V |
Ammeter | 1 mA – 0.1 A | 0 – 10 A |
Oscilloscope | 1 Hz | 0 – 200 MHz |
These are just examples of ranges and resolutions for these devices
For example, some multimeters may have a bigger or smaller range depending on their model
The resolution of an instrument gives its absolute uncertainty for a digital device
For an analogue device, such as a thermometer, ruler or top-pan balance, the uncertainty is ± half the resolution
Worked Example
The diagram below shows one possible method for determining the Young modulus of a metal in the form of a wire.
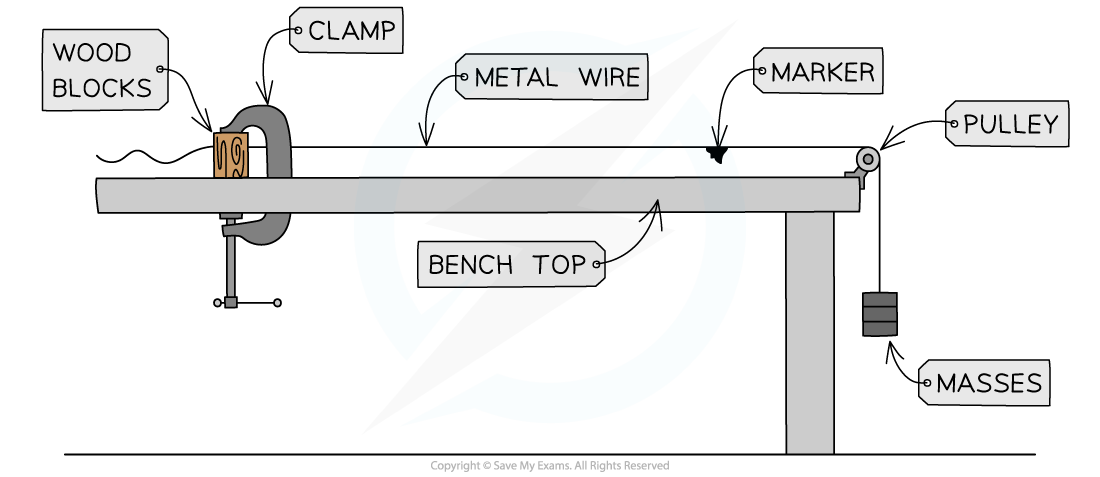
Describe how you can use this apparatus to determine the Young modulus of the metal. The sections below should be helpful when writing your answers.
The measurements to be taken.
The equipment used to take the measurements.
How you would determine Young modulus from your measurements.
Answer:
Step 1: State the necessary measurements to be taken
The diameter of the wire
The initial length of the wire
The extension of the wire (final length – initial length)
The mass of the hanging masses or the weight applied to the wire
Step 2: State and explain which equipment would be the most suitable
For measuring the diameter of the wire:
A micrometer screw gauge or vernier callipers
Micrometer would be best as this has the highest resolution when measuring small areas
For measuring the original length / extension of the wire:
A metre ruler or a tape measure
The wire has a moderate length which cannot be measured using a vernier scale
For measuring extension:
Travelling microscope
These are designed for measuring small changes in length
For measuring the mass:
Scales or a top-pan balance
A top-pan balance would be best as this has the higher resolution
W = mg equation can be used to calculate weight
For measuring the weight directly:
A newton-meter
This is useful if ‘known’ weights are used and to check if the quoted masses are accurate
Step 3: Explain how Young's modulus can be determined from these measurements
Young modulus is equal to the gradient of a stress-strain graph (in the linear region)
Stress is equal to:

Strain is equal to:

Where:
F = weight (N)
A = cross-sectional area of wire (m2)
ΔL = extension (m)
L = original length (m)
Young's modulus for this metal is then calculated using the following equation:
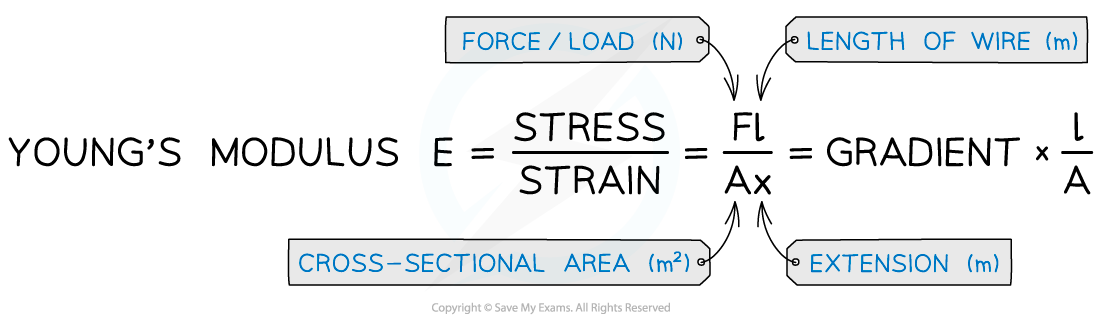
Worked Example
Two digital thermometers display a reading in °C.
Thermometer 1: 80.13 °C
Thermometer 2: 42.0 °C
Which thermometer has the better resolution?
Answer:
The resolution is given by the smallest increment that the thermometer can read
For thermometer 1 this is 0.01 °C
For thermometer 2 this is 0.1 °C
Therefore, thermometer 1 has the better resolution
Examiner Tips and Tricks
Exam questions can refer to different instrument with various ranges and resolutions, for example, ammeters with resolution of 0.2 mA instead. Always use the information given in the question, and look carefully at the scales given. Never just assume the resolution of a piece of instrument given in an exam question.
When listing the apparatus for an experiment, make sure you've referred to every last piece of equipment, even the small parts such as wires and power supplies

Unlock more, it's free!
Did this page help you?