Trend & Patterns in Experimental Data (Edexcel International A Level (IAL) Physics) : Revision Note
Trend & Patterns in Experimental Data
Graphs are used to visualise the relationship between two sets of data from two different variables
Trends and patterns can be identified from experimental data
Common trends are:
Linear
Directly proportional
Inversely proportional
Rate of change
A linear graph set of data is any data that creates a straight line

An example of a linear graph
The rate of change of a graph is how quickly a variable is increasing or decreasing with something else
This can be seen from the change in gradient of the graph, an increasing gradient has an increasing rate of change and a decreasing gradient has a decreasing rate of change
A direct proportionality relationship is where as one amount increases, another amount increases at the same rate
This is represented by a straight-line graph with a positive gradient
For two variables, y and x this looks like:
y ∝ x
An inverse proportionality relationship is where as one amount increases, another amount decreases at the same rate
This is represented by a curved graph with a decreasing gradient
For two variables, y and x this looks like:
y ∝

Sketched graphs show relationships between variables
In the first sketch graph, above you can see that the relationship is a straight line going through the origin
This means as you double one variable the other variable also doubles so we say the independent variable is directly proportional to the dependent variable
The second sketched graph shows a shallow curve
This is the characteristic shape when two variables have an inversely proportional relationship
The third sketched graph shows a straight horizontal line,
This means as the independent variable (x-axis) increases the dependent variable does not change or is constant
Worked Example
Comment on the trend of the graph.
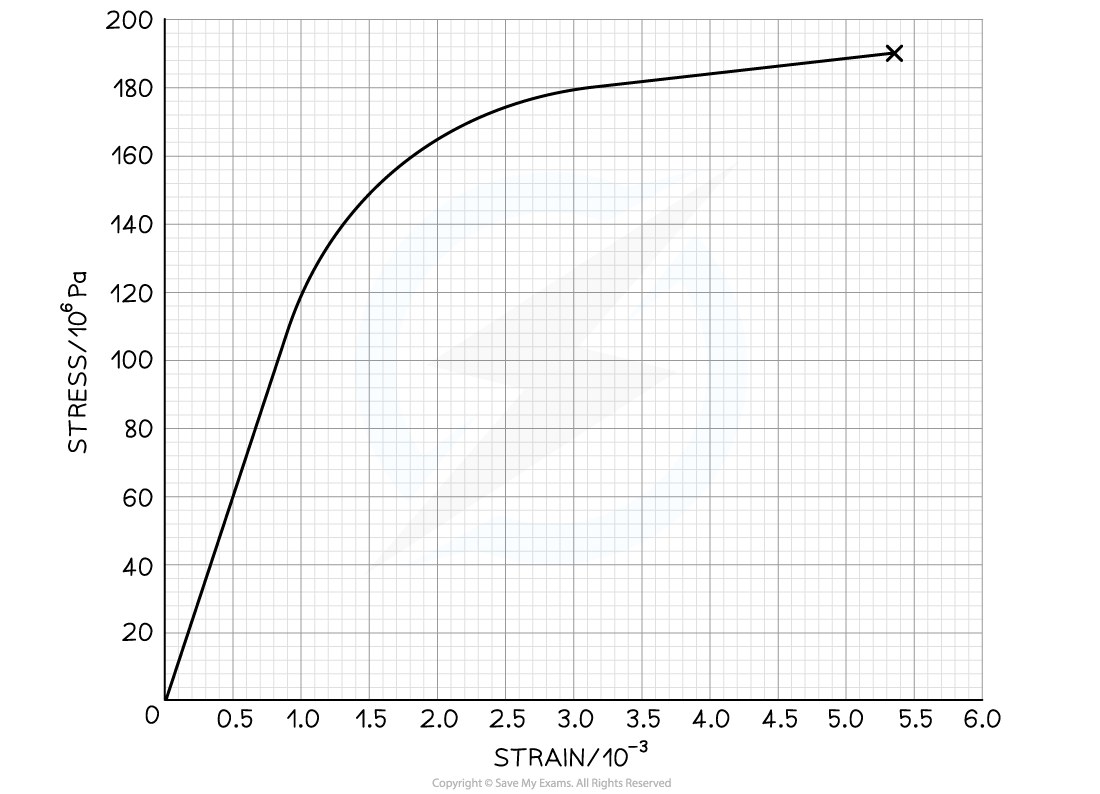
Answer:
Stress and strain are proportional to each other, but not directly
The graph is linear with a positive gradient up to a strain of 1.0 × 10-3
After this, the rate of change of the strain with stress decreases, as the gradient of the graph decreases up to the breaking stress at 190 MPa

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
