Period of Simple Harmonic Oscillators (Edexcel International A Level Physics)

• A simple pendulum is: 
  • An object moving from side to side
  • Attached to a fixed point above 

• The time period of a simple pendulum can also be calculated using this equation:

T = 2π

• Where: 
  • l is the length of the pendulum swing
  • g is the strength of gravity on the planet on which the pendulum is set up

Step 1: Convert length to meters

200 cm = 2 m

Step 2: Substitute the correct values

T = 2π= 2π=2.84 s 

Step 3: Confirm the answer

The time period of 1 oscillation of the swing is 2.84 s

• A mass-spring system means:
  • An object moving up and down 
  • On the end of a spring

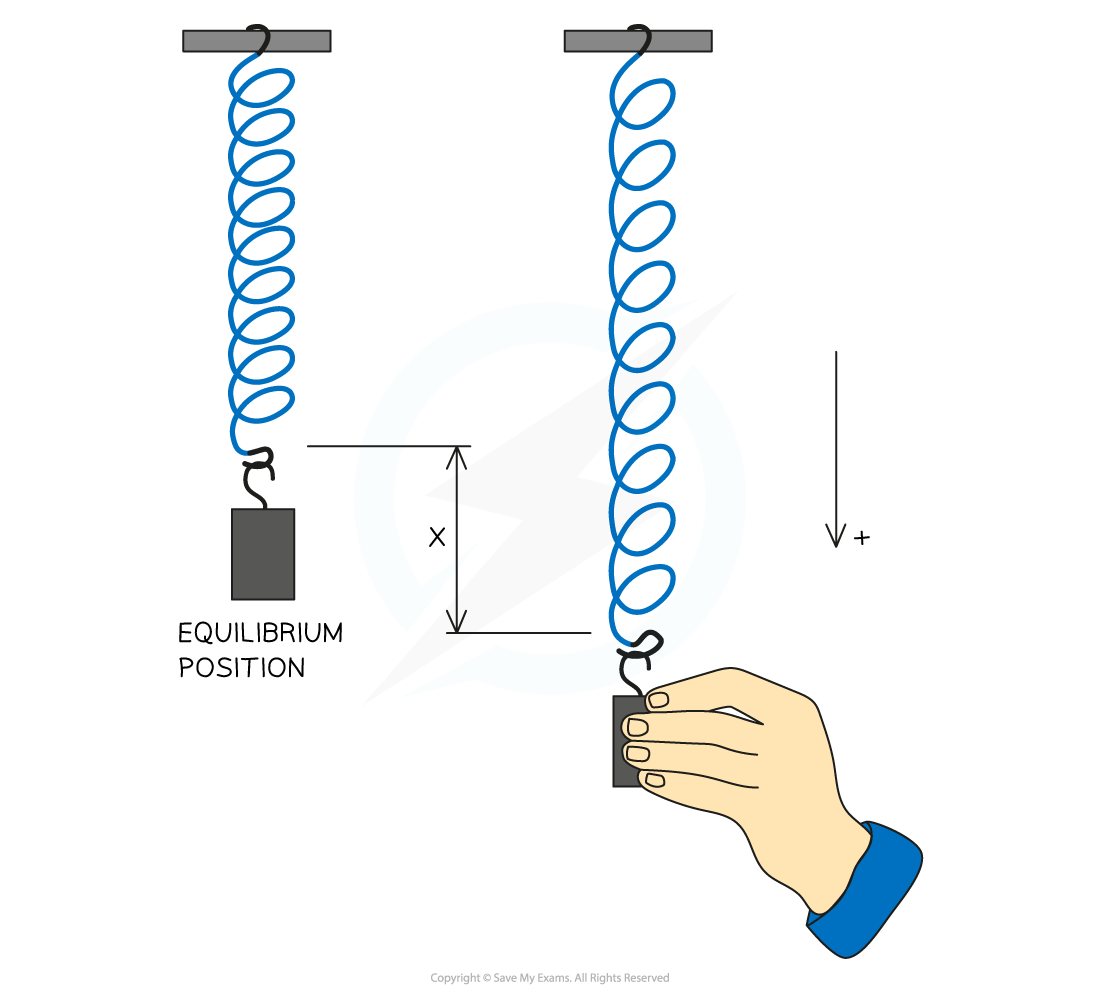
• The equation for the restoring force in SHM F = - kx 
  • is the same as the equation for Hooke's Law
• The time period, T can be calculated using the equation:

T = 2π

• Where: 
  • m is the mass of the object on the end of the pendulum
  • k is the spring constant of the material the pendulum is made from

Observing the Motion of a Mass-Spring System

• An experimental and graphical method can be used to observe the motion of a simple mass-spring system
  • Tie a pencil together with the mass and set the mass in free oscillations by displacing it downwards slightly

• The oscillations will move the pencil up and down
  • On a piece of graph paper, allow the pencil to trace the path of the oscillations by pulling the paper sideways as the mass-spring system oscillates up and down

• The oscillations will produce a curved, periodic graph
  • This will decrease in amplitude as the mass-spring system slows down

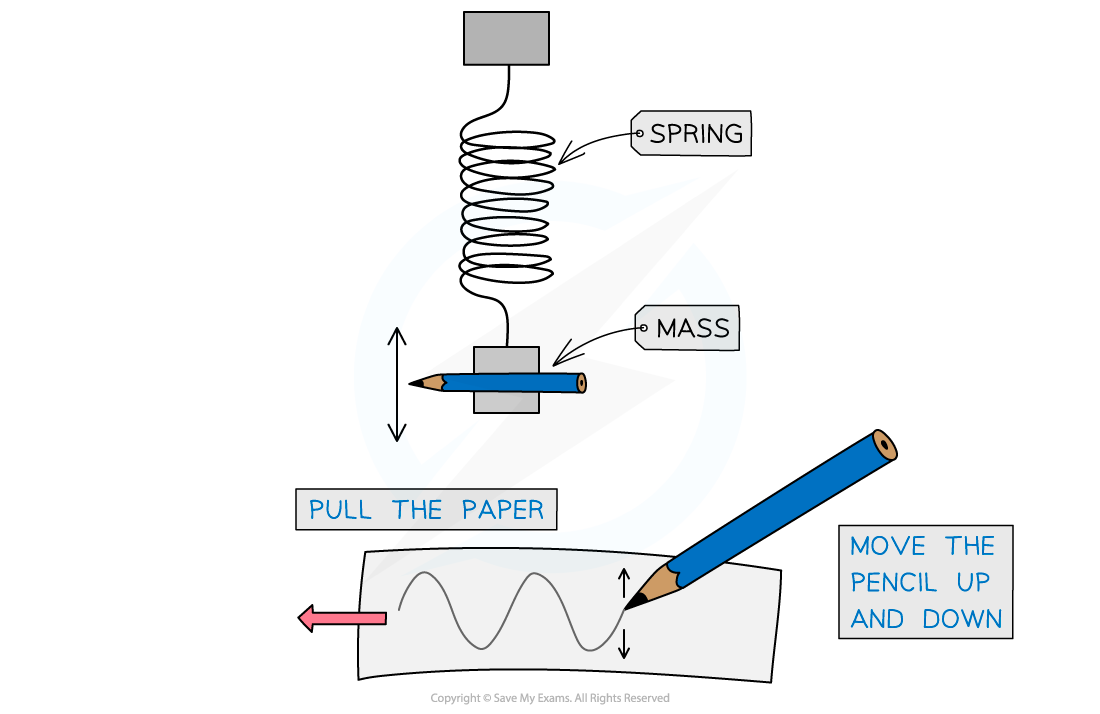
The motion of oscillator can be observed through a simple mass and spring system